Question Number 63438 by ajfour last updated on 04/Jul/19
Commented by ajfour last updated on 04/Jul/19

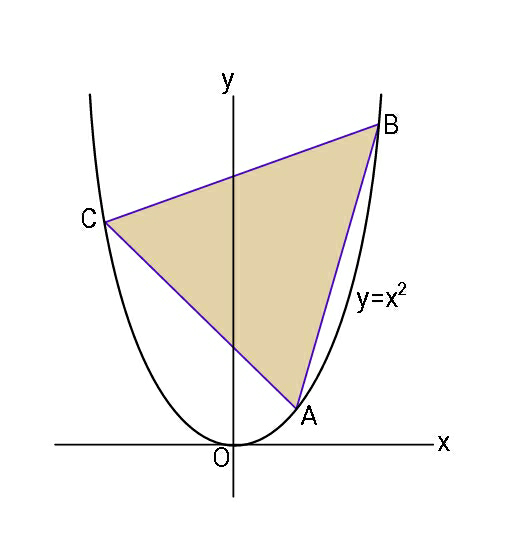
$${Determine}\:\:{a}:{b}:{c}\:\:{if}\:{the} \\ $$$${inscribed}\:\bigtriangleup{ABC}\:{has}\:{constant} \\ $$$${perimeter}\:{but}\:{maximum}\:{area}. \\ $$
Commented by ajfour last updated on 04/Jul/19
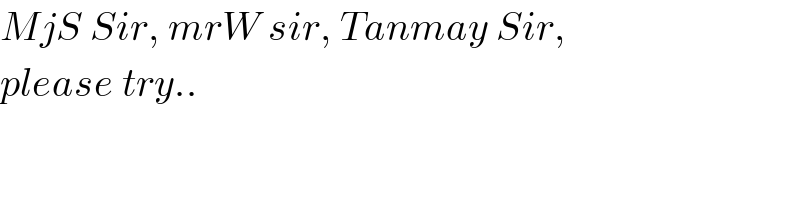
$${MjS}\:{Sir},\:{mrW}\:{sir},\:{Tanmay}\:{Sir}, \\ $$$${please}\:{try}.. \\ $$
Answered by ajfour last updated on 04/Jul/19
![A(h,h^2 ) B(h+ccos θ, h^2 +csin θ) C(h+bcos φ, h^2 +bsin φ) a+b+c=p ......(i) h^2 +csin θ=(h+ccos θ)^2 ...(ii) ⇒ sin θ=ccos^2 θ+2hcos θ ⇒ ccos θ=tan θ−2h h^2 +bsin φ=(h+bcos φ)^2 ....(iii) ⇒ bcos φ=tan φ−2h (ccos θ−bcos φ)^2 +(csin θ−bsin φ)^2 =a^2 .....(iv) ⇒ b^2 +c^2 −a^2 =2bccos (φ−θ) ⇒ −p^2 −2(b+c)p=2bccos (φ−θ) −p^2 −2p[((tan θ−2h)/(cos θ))+((tan φ−2h)/(cos φ))] = 2(tan θ−2h)(tan φ−2h)(1+tan θtan φ) △=((cd)/2) d=b(sin φ−cos φtan θ)cos θ ⇒ △=((bc)/2)(bsin φ−bcos φtan θ)cos θ △=((bc)/2)sin (φ−θ) 2△=(((tan θ−2h)(tan φ−2h)sin (φ−θ))/(cos θcos φ)) 2△=(tan θ−2h)(tan φ−2h)(tan φ−tan θ) −p^2 −2p[((tan θ−2h)/(cos θ))+((tan φ−2h)/(cos φ))] = 2(tan θ−2h)(tan φ−2h)(1+tan θtan φ) Now let tan θ=t, tan φ=s ⇒ −p^2 −2p[(t−2h)(√(1+t^2 ))+(s−2h)(√(1+s^2 )) ] =2(t−2h)(s−2h)(1+st) but i′m afraid its not going to yield!](https://www.tinkutara.com/question/Q63469.png)
$${A}\left({h},{h}^{\mathrm{2}} \right) \\ $$$${B}\left({h}+{c}\mathrm{cos}\:\theta,\:{h}^{\mathrm{2}} +{c}\mathrm{sin}\:\theta\right) \\ $$$${C}\left({h}+{b}\mathrm{cos}\:\phi,\:{h}^{\mathrm{2}} +{b}\mathrm{sin}\:\phi\right) \\ $$$${a}+{b}+{c}={p}\:\:\:\:\:\:\:\:\:\:\:\:\:……\left({i}\right) \\ $$$${h}^{\mathrm{2}} +{c}\mathrm{sin}\:\theta=\left({h}+{c}\mathrm{cos}\:\theta\right)^{\mathrm{2}} \:\:\:\:\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\theta={c}\mathrm{cos}\:^{\mathrm{2}} \theta+\mathrm{2}{h}\mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\:{c}\mathrm{cos}\:\theta=\mathrm{tan}\:\theta−\mathrm{2}{h} \\ $$$${h}^{\mathrm{2}} +{b}\mathrm{sin}\:\phi=\left({h}+{b}\mathrm{cos}\:\phi\right)^{\mathrm{2}} \:\:\:\:\:\:….\left({iii}\right) \\ $$$$\Rightarrow\:\:{b}\mathrm{cos}\:\phi=\mathrm{tan}\:\phi−\mathrm{2}{h} \\ $$$$\left({c}\mathrm{cos}\:\theta−{b}\mathrm{cos}\:\phi\right)^{\mathrm{2}} +\left({c}\mathrm{sin}\:\theta−{b}\mathrm{sin}\:\phi\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…..\left({iv}\right) \\ $$$$\Rightarrow\:{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} =\mathrm{2}{bc}\mathrm{cos}\:\left(\phi−\theta\right) \\ $$$$\Rightarrow\:−{p}^{\mathrm{2}} −\mathrm{2}\left({b}+{c}\right){p}=\mathrm{2}{bc}\mathrm{cos}\:\left(\phi−\theta\right) \\ $$$$−{p}^{\mathrm{2}} −\mathrm{2}{p}\left[\frac{\mathrm{tan}\:\theta−\mathrm{2}{h}}{\mathrm{cos}\:\theta}+\frac{\mathrm{tan}\:\phi−\mathrm{2}{h}}{\mathrm{cos}\:\phi}\right] \\ $$$$\:\:\:\:\:\:\:=\:\mathrm{2}\left(\mathrm{tan}\:\theta−\mathrm{2}{h}\right)\left(\mathrm{tan}\:\phi−\mathrm{2}{h}\right)\left(\mathrm{1}+\mathrm{tan}\:\theta\mathrm{tan}\:\phi\right) \\ $$$$\bigtriangleup=\frac{{cd}}{\mathrm{2}} \\ $$$${d}={b}\left(\mathrm{sin}\:\phi−\mathrm{cos}\:\phi\mathrm{tan}\:\theta\right)\mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\bigtriangleup=\frac{{bc}}{\mathrm{2}}\left({b}\mathrm{sin}\:\phi−{b}\mathrm{cos}\:\phi\mathrm{tan}\:\theta\right)\mathrm{cos}\:\theta \\ $$$$\bigtriangleup=\frac{{bc}}{\mathrm{2}}\mathrm{sin}\:\left(\phi−\theta\right) \\ $$$$\mathrm{2}\bigtriangleup=\frac{\left(\mathrm{tan}\:\theta−\mathrm{2}{h}\right)\left(\mathrm{tan}\:\phi−\mathrm{2}{h}\right)\mathrm{sin}\:\left(\phi−\theta\right)}{\mathrm{cos}\:\theta\mathrm{cos}\:\phi} \\ $$$$\mathrm{2}\bigtriangleup=\left(\mathrm{tan}\:\theta−\mathrm{2}{h}\right)\left(\mathrm{tan}\:\phi−\mathrm{2}{h}\right)\left(\mathrm{tan}\:\phi−\mathrm{tan}\:\theta\right) \\ $$$$−{p}^{\mathrm{2}} −\mathrm{2}{p}\left[\frac{\mathrm{tan}\:\theta−\mathrm{2}{h}}{\mathrm{cos}\:\theta}+\frac{\mathrm{tan}\:\phi−\mathrm{2}{h}}{\mathrm{cos}\:\phi}\right] \\ $$$$\:\:\:\:\:\:\:=\:\mathrm{2}\left(\mathrm{tan}\:\theta−\mathrm{2}{h}\right)\left(\mathrm{tan}\:\phi−\mathrm{2}{h}\right)\left(\mathrm{1}+\mathrm{tan}\:\theta\mathrm{tan}\:\phi\right) \\ $$$${Now}\:{let}\:\:\mathrm{tan}\:\theta={t},\:\:\mathrm{tan}\:\phi={s} \\ $$$$\Rightarrow\:\:−{p}^{\mathrm{2}} −\mathrm{2}{p}\left[\left({t}−\mathrm{2}{h}\right)\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }+\left({s}−\mathrm{2}{h}\right)\sqrt{\mathrm{1}+{s}^{\mathrm{2}} }\:\right] \\ $$$$\:\:\:=\mathrm{2}\left({t}−\mathrm{2}{h}\right)\left({s}−\mathrm{2}{h}\right)\left(\mathrm{1}+{st}\right) \\ $$$${but}\:{i}'{m}\:{afraid}\:{its}\:{not}\:{going}\:{to}\:{yield}! \\ $$
Commented by ajfour last updated on 04/Jul/19
![−p^2 −2p[((tan θ−2h)/(cos θ))+((tan φ−2h)/(cos φ))] = 2(tan θ−2h)(tan φ−2h)(1+tan θtan φ) ........(I) 2△=(tan θ−2h)(tan φ−2h)(tan φ−tan θ) ........(II) To find θ,φ such that △ is max.](https://www.tinkutara.com/question/Q63471.png)
$$−{p}^{\mathrm{2}} −\mathrm{2}{p}\left[\frac{\mathrm{tan}\:\theta−\mathrm{2}{h}}{\mathrm{cos}\:\theta}+\frac{\mathrm{tan}\:\phi−\mathrm{2}{h}}{\mathrm{cos}\:\phi}\right] \\ $$$$\:\:\:\:\:\:\:=\:\mathrm{2}\left(\mathrm{tan}\:\theta−\mathrm{2}{h}\right)\left(\mathrm{tan}\:\phi−\mathrm{2}{h}\right)\left(\mathrm{1}+\mathrm{tan}\:\theta\mathrm{tan}\:\phi\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……..\left({I}\right) \\ $$$$\mathrm{2}\bigtriangleup=\left(\mathrm{tan}\:\theta−\mathrm{2}{h}\right)\left(\mathrm{tan}\:\phi−\mathrm{2}{h}\right)\left(\mathrm{tan}\:\phi−\mathrm{tan}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……..\left({II}\right) \\ $$$${To}\:{find}\:\theta,\phi\:{such}\:{that}\:\bigtriangleup\:{is}\:{max}. \\ $$
Commented by mr W last updated on 04/Jul/19
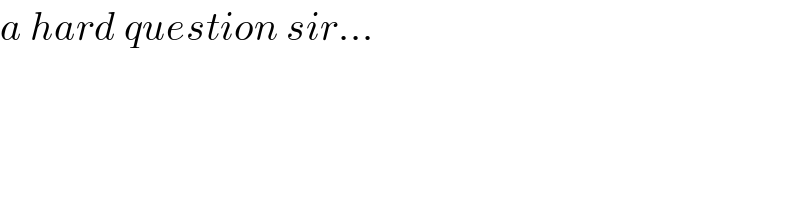
$${a}\:{hard}\:{question}\:{sir}… \\ $$
