Question Number 63642 by bshahid010@gmail.com last updated on 06/Jul/19
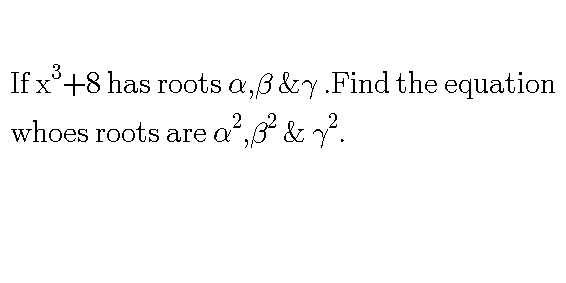
Commented by kaivan.ahmadi last updated on 06/Jul/19
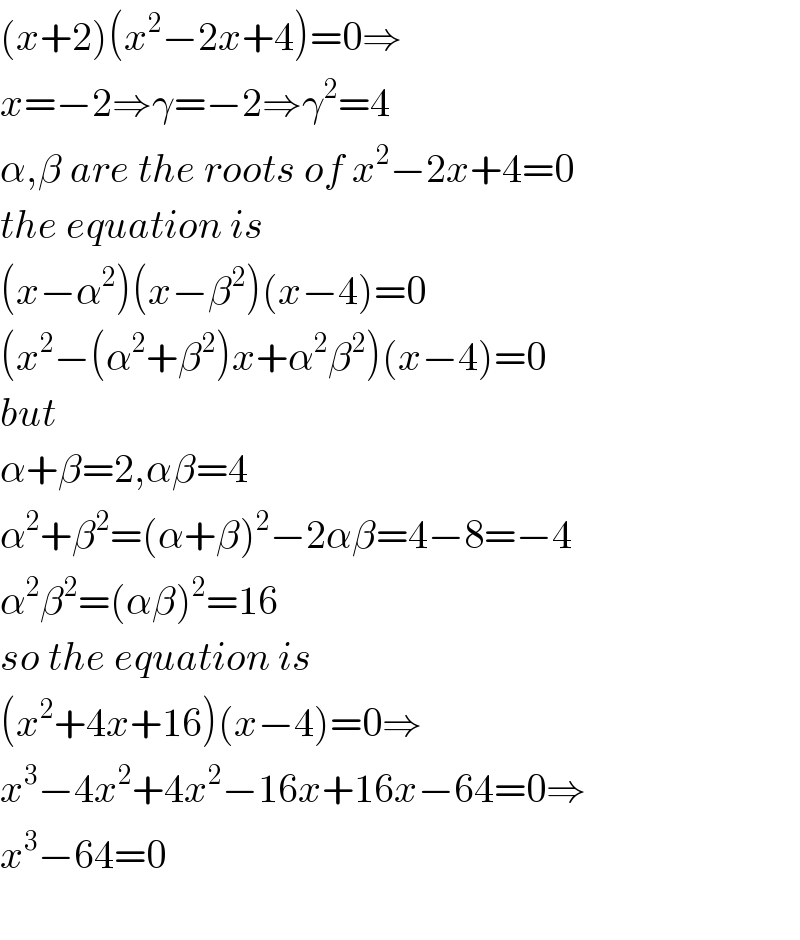
$$\left({x}+\mathrm{2}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}\right)=\mathrm{0}\Rightarrow \\ $$$${x}=−\mathrm{2}\Rightarrow\gamma=−\mathrm{2}\Rightarrow\gamma^{\mathrm{2}} =\mathrm{4} \\ $$$$\alpha,\beta\:{are}\:{the}\:{roots}\:{of}\:{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}=\mathrm{0} \\ $$$${the}\:{equation}\:{is} \\ $$$$\left({x}−\alpha^{\mathrm{2}} \right)\left({x}−\beta^{\mathrm{2}} \right)\left({x}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right){x}+\alpha^{\mathrm{2}} \beta^{\mathrm{2}} \right)\left({x}−\mathrm{4}\right)=\mathrm{0} \\ $$$${but}\: \\ $$$$\alpha+\beta=\mathrm{2},\alpha\beta=\mathrm{4} \\ $$$$\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} =\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{2}\alpha\beta=\mathrm{4}−\mathrm{8}=−\mathrm{4} \\ $$$$\alpha^{\mathrm{2}} \beta^{\mathrm{2}} =\left(\alpha\beta\right)^{\mathrm{2}} =\mathrm{16} \\ $$$${so}\:{the}\:{equation}\:{is} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{16}\right)\left({x}−\mathrm{4}\right)=\mathrm{0}\Rightarrow \\ $$$${x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}+\mathrm{16}{x}−\mathrm{64}=\mathrm{0}\Rightarrow \\ $$$${x}^{\mathrm{3}} −\mathrm{64}=\mathrm{0} \\ $$$$ \\ $$
Answered by MJS last updated on 06/Jul/19

$${x}^{\mathrm{3}} −\mathrm{8}^{\mathrm{2}} =\mathrm{0} \\ $$
Answered by MJS last updated on 06/Jul/19

$${x}^{\mathrm{3}} =−\mathrm{8} \\ $$$${x}_{\mathrm{1}} =−\mathrm{2}\:\Rightarrow\:{x}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{4} \\ $$$${x}_{\mathrm{2}} =\mathrm{2e}^{\mathrm{i}\frac{\pi}{\mathrm{3}}} \:\Rightarrow\:{x}_{\mathrm{2}} ^{\mathrm{2}} =\mathrm{4e}^{\mathrm{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \\ $$$${x}_{\mathrm{3}} =\mathrm{2e}^{−\mathrm{i}\frac{\pi}{\mathrm{3}}} \:\Rightarrow\:{x}_{\mathrm{3}} ^{\mathrm{2}} =\mathrm{4e}^{−\mathrm{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \\ $$$$\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:{x}_{\mathrm{1}} ^{\mathrm{3}} =\mathrm{64}\:\Rightarrow\:\mathrm{the}\:\mathrm{equation}\:\mathrm{is} \\ $$$${x}^{\mathrm{3}} =\mathrm{64} \\ $$$$\mathrm{to}\:\mathrm{be}\:\mathrm{sure}: \\ $$$$\left({x}−\mathrm{4}\right)\left({x}−\mathrm{4e}^{\mathrm{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \right)\left({x}−\mathrm{4e}^{−\mathrm{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \right)= \\ $$$$=\left({x}−\mathrm{4}\right)\left({x}^{\mathrm{2}} −\mathrm{4}{x}\left(\mathrm{e}^{\mathrm{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} +\mathrm{e}^{−\mathrm{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \right)+\mathrm{16}\right)= \\ $$$$=\left({x}−\mathrm{4}\right)\left({x}^{\mathrm{2}} −\mathrm{4}{x}\left(−\mathrm{1}\right)+\mathrm{16}\right)= \\ $$$$=\left({x}−\mathrm{4}\right)\left({x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{16}\right)={x}^{\mathrm{3}} −\mathrm{64} \\ $$
