Question Number 63663 by Tawa1 last updated on 07/Jul/19
Answered by mr W last updated on 07/Jul/19

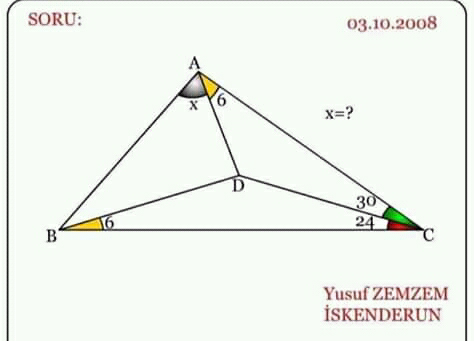
$$\angle{ADB}=\mathrm{360}−\left(\mathrm{180}−\mathrm{6}−\mathrm{30}\right)−\left(\mathrm{180}−\mathrm{6}−\mathrm{24}\right)=\mathrm{66}° \\ $$$$\frac{{AD}}{{DC}}=\frac{\mathrm{sin}\:\mathrm{30}°}{\mathrm{sin}\:\mathrm{6}°} \\ $$$$\frac{{BD}}{{DC}}=\frac{\mathrm{sin}\:\mathrm{24}°}{\mathrm{sin}\:\mathrm{6}°} \\ $$$$\Rightarrow\frac{{AD}}{{BD}}=\frac{\mathrm{sin}\:\mathrm{30}°}{\mathrm{sin}\:\mathrm{24}°} \\ $$$$\frac{{AD}}{{BD}}=\frac{\mathrm{sin}\:\left(\angle{ADB}+{x}\right)}{\mathrm{sin}\:{x}}=\frac{\mathrm{sin}\:\left(\mathrm{66}+{x}\right)}{\mathrm{sin}\:{x}} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\mathrm{30}°}{\mathrm{sin}\:\mathrm{24}°}=\frac{\mathrm{sin}\:\left(\mathrm{66}+{x}\right)}{\mathrm{sin}\:{x}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{24}°}=\frac{\mathrm{sin}\:\mathrm{66}°}{\mathrm{tan}\:{x}}+\mathrm{cos}\:\mathrm{66}° \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\mathrm{66}°}{\mathrm{tan}\:{x}}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{24}°}−\mathrm{sin}\:\mathrm{24}° \\ $$$$\Rightarrow\frac{\mathrm{cos}\:\mathrm{24}°}{\mathrm{tan}\:{x}}=\frac{\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{24}°}{\mathrm{2}\:\mathrm{sin}\:\mathrm{24}°} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{tan}\:{x}}=\frac{\mathrm{cos}\:\mathrm{48}°}{\mathrm{2}\:\mathrm{sin}\:\mathrm{24}°\:\mathrm{cos}\:\mathrm{24}°} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{tan}\:{x}}=\frac{\mathrm{cos}\:\mathrm{48}°}{\mathrm{sin}\:\mathrm{48}°} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{tan}\:{x}}=\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{48}°} \\ $$$$\Rightarrow{x}=\mathrm{48}° \\ $$
Commented by Tawa1 last updated on 07/Jul/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 07/Jul/19

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir} \\ $$
