Question-63769

Question Number 63769 by aliesam last updated on 08/Jul/19

Commented by mathmax by abdo last updated on 09/Jul/19

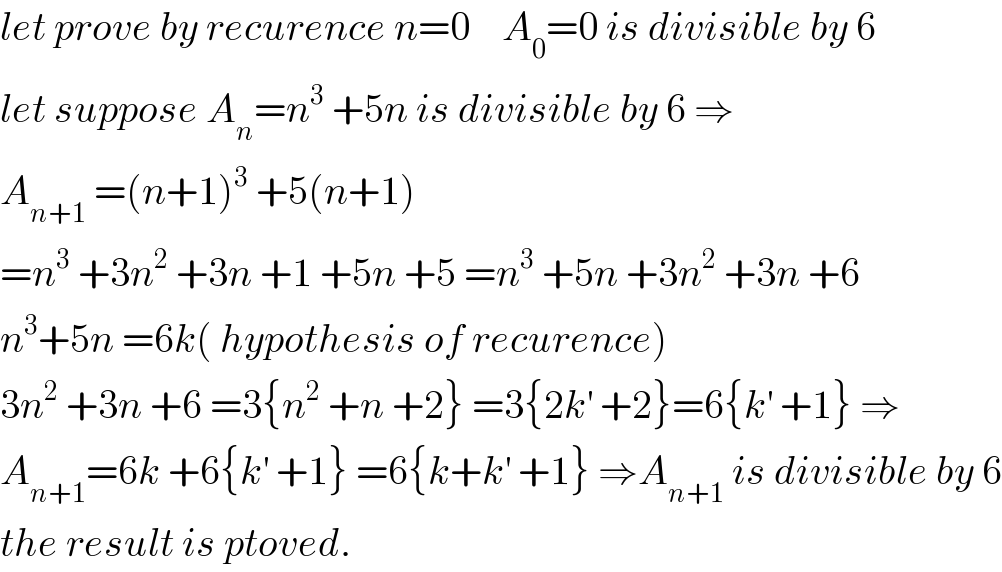
let prove by recurence n=0 A_0 =0 is divisible by 6 let suppose A_n =n^3 +5n is divisible by 6 ⇒ A_(n+1) =(n+1)^3 +5(n+1) =n^3 +3n^2 +3n +1 +5n +5 =n^3 +5n +3n^2 +3n +6 n^3 +5n =6k( hypothesis of recurence) 3n^2 +3n +6 =3{n^2 +n +2} =3{2k^′ +2}=6{k^′ +1} ⇒ A_(n+1) =6k +6{k^′ +1} =6{k+k^′ +1} ⇒A_(n+1) is divisible by 6 the result is ptoved.

$${let}\:{prove}\:{by}\:{recurence}\:{n}=\mathrm{0}\:\:\:\:{A}_{\mathrm{0}} =\mathrm{0}\:{is}\:{divisible}\:{by}\:\mathrm{6} \\ $$$${let}\:{suppose}\:{A}_{{n}} ={n}^{\mathrm{3}} \:+\mathrm{5}{n}\:{is}\:{divisible}\:{by}\:\mathrm{6}\:\Rightarrow \\ $$$${A}_{{n}+\mathrm{1}} \:=\left({n}+\mathrm{1}\right)^{\mathrm{3}} \:+\mathrm{5}\left({n}+\mathrm{1}\right) \\ $$$$={n}^{\mathrm{3}} \:+\mathrm{3}{n}^{\mathrm{2}} \:+\mathrm{3}{n}\:+\mathrm{1}\:+\mathrm{5}{n}\:+\mathrm{5}\:={n}^{\mathrm{3}} \:+\mathrm{5}{n}\:+\mathrm{3}{n}^{\mathrm{2}} \:+\mathrm{3}{n}\:+\mathrm{6} \\ $$$${n}^{\mathrm{3}} +\mathrm{5}{n}\:=\mathrm{6}{k}\left(\:{hypothesis}\:{of}\:{recurence}\right) \\ $$$$\mathrm{3}{n}^{\mathrm{2}} \:+\mathrm{3}{n}\:+\mathrm{6}\:=\mathrm{3}\left\{{n}^{\mathrm{2}} \:+{n}\:+\mathrm{2}\right\}\:=\mathrm{3}\left\{\mathrm{2}{k}^{'} \:+\mathrm{2}\right\}=\mathrm{6}\left\{{k}^{'} \:+\mathrm{1}\right\}\:\Rightarrow \\ $$$${A}_{{n}+\mathrm{1}} =\mathrm{6}{k}\:+\mathrm{6}\left\{{k}^{'} \:+\mathrm{1}\right\}\:=\mathrm{6}\left\{{k}+{k}^{'} \:+\mathrm{1}\right\}\:\Rightarrow{A}_{{n}+\mathrm{1}} \:{is}\:{divisible}\:{by}\:\mathrm{6} \\ $$$${the}\:{result}\:{is}\:{ptoved}. \\ $$

Answered by MJS last updated on 08/Jul/19

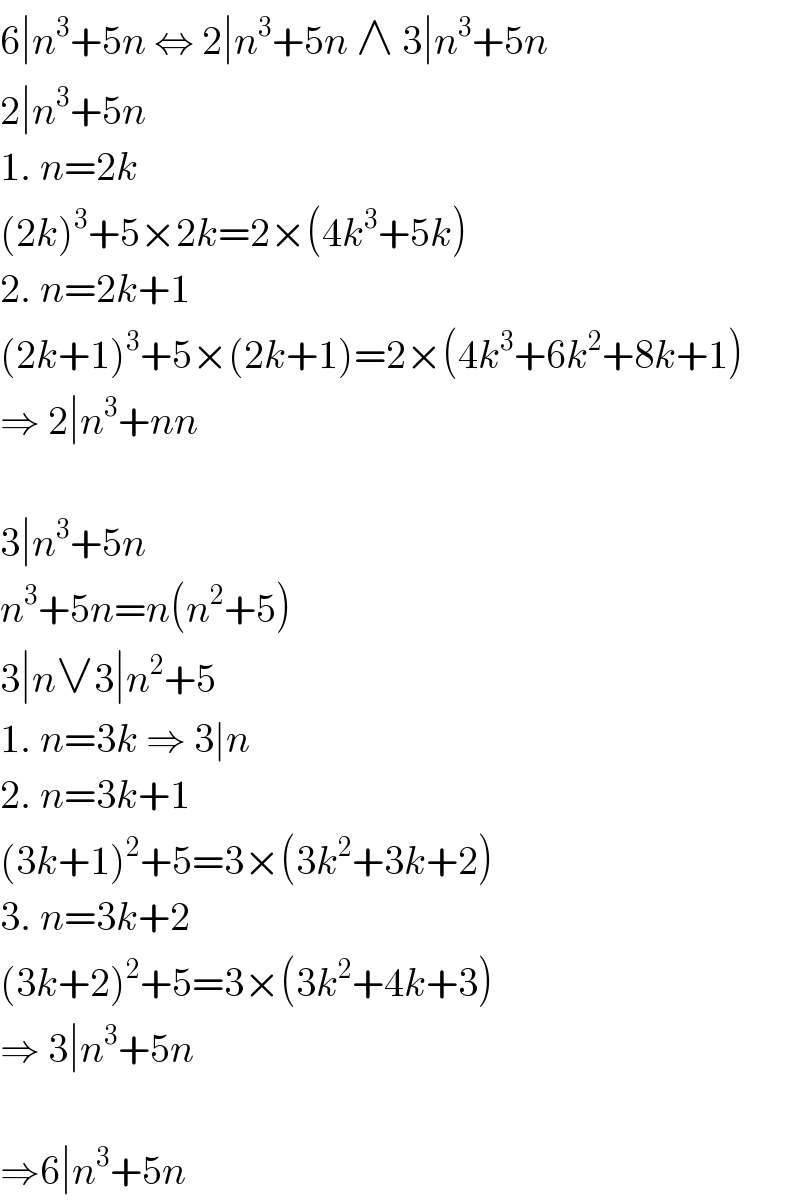
6∣n^3 +5n ⇔ 2∣n^3 +5n ∧ 3∣n^3 +5n 2∣n^3 +5n 1. n=2k (2k)^3 +5×2k=2×(4k^3 +5k) 2. n=2k+1 (2k+1)^3 +5×(2k+1)=2×(4k^3 +6k^2 +8k+1) ⇒ 2∣n^3 +nn 3∣n^3 +5n n^3 +5n=n(n^2 +5) 3∣n∨3∣n^2 +5 1. n=3k ⇒ 3∣n 2. n=3k+1 (3k+1)^2 +5=3×(3k^2 +3k+2) 3. n=3k+2 (3k+2)^2 +5=3×(3k^2 +4k+3) ⇒ 3∣n^3 +5n ⇒6∣n^3 +5n

$$\mathrm{6}\mid{n}^{\mathrm{3}} +\mathrm{5}{n}\:\Leftrightarrow\:\mathrm{2}\mid{n}^{\mathrm{3}} +\mathrm{5}{n}\:\wedge\:\mathrm{3}\mid{n}^{\mathrm{3}} +\mathrm{5}{n} \\ $$$$\mathrm{2}\mid{n}^{\mathrm{3}} +\mathrm{5}{n} \\ $$$$\mathrm{1}.\:{n}=\mathrm{2}{k} \\ $$$$\left(\mathrm{2}{k}\right)^{\mathrm{3}} +\mathrm{5}×\mathrm{2}{k}=\mathrm{2}×\left(\mathrm{4}{k}^{\mathrm{3}} +\mathrm{5}{k}\right) \\ $$$$\mathrm{2}.\:{n}=\mathrm{2}{k}+\mathrm{1} \\ $$$$\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{3}} +\mathrm{5}×\left(\mathrm{2}{k}+\mathrm{1}\right)=\mathrm{2}×\left(\mathrm{4}{k}^{\mathrm{3}} +\mathrm{6}{k}^{\mathrm{2}} +\mathrm{8}{k}+\mathrm{1}\right) \\ $$$$\Rightarrow\:\mathrm{2}\mid{n}^{\mathrm{3}} +{nn} \\ $$$$ \\ $$$$\mathrm{3}\mid{n}^{\mathrm{3}} +\mathrm{5}{n} \\ $$$${n}^{\mathrm{3}} +\mathrm{5}{n}={n}\left({n}^{\mathrm{2}} +\mathrm{5}\right) \\ $$$$\mathrm{3}\mid{n}\vee\mathrm{3}\mid{n}^{\mathrm{2}} +\mathrm{5} \\ $$$$\mathrm{1}.\:{n}=\mathrm{3}{k}\:\Rightarrow\:\mathrm{3}\mid{n} \\ $$$$\mathrm{2}.\:{n}=\mathrm{3}{k}+\mathrm{1} \\ $$$$\left(\mathrm{3}{k}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{5}=\mathrm{3}×\left(\mathrm{3}{k}^{\mathrm{2}} +\mathrm{3}{k}+\mathrm{2}\right) \\ $$$$\mathrm{3}.\:{n}=\mathrm{3}{k}+\mathrm{2} \\ $$$$\left(\mathrm{3}{k}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{5}=\mathrm{3}×\left(\mathrm{3}{k}^{\mathrm{2}} +\mathrm{4}{k}+\mathrm{3}\right) \\ $$$$\Rightarrow\:\mathrm{3}\mid{n}^{\mathrm{3}} +\mathrm{5}{n} \\ $$$$ \\ $$$$\Rightarrow\mathrm{6}\mid{n}^{\mathrm{3}} +\mathrm{5}{n} \\ $$

Commented by aliesam last updated on 09/Jul/19

$${god}\:{bless}\:{you} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply