Question Number 63981 by ajfour last updated on 11/Jul/19
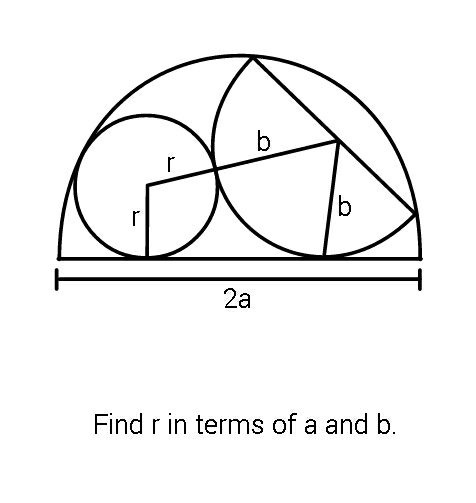
Answered by mr W last updated on 11/Jul/19
![[(√(a^2 −b^2 −b^2 ))+(√((a−r)^2 −r^2 ))]^2 =(b+r)^2 −(b−r)^2 −b^2 +a(a−r)+(√((a^2 −2b^2 )a(a−2r)))=2br (√((a^2 −2b^2 )a(a−2r)))=(a+2b)r−(a^2 −b^2 ) (a^2 −2b^2 )a(a−2r)=(a+2b)^2 r^2 +(a^2 −b^2 )^2 −2(a+2b)(a^2 −b^2 )r (a+2b)^2 r^2 −2[2(a^3 −b^3 )+ab(2a−3b)]r+b^4 =0 ⇒r=((2(a^3 −b^3 )+ab(2a−3b)+(√([2(a^3 −b^3 )+ab(2a−3b)]^2 −(a+2b)^2 b^4 )))/((a+2b)^2 ))](https://www.tinkutara.com/question/Q63992.png)
$$\left[\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −{b}^{\mathrm{2}} }+\sqrt{\left({a}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }\right]^{\mathrm{2}} =\left({b}+{r}\right)^{\mathrm{2}} −\left({b}−{r}\right)^{\mathrm{2}} \\ $$$$−{b}^{\mathrm{2}} +{a}\left({a}−{r}\right)+\sqrt{\left({a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} \right){a}\left({a}−\mathrm{2}{r}\right)}=\mathrm{2}{br} \\ $$$$\sqrt{\left({a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} \right){a}\left({a}−\mathrm{2}{r}\right)}=\left({a}+\mathrm{2}{b}\right){r}−\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right) \\ $$$$\left({a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} \right){a}\left({a}−\mathrm{2}{r}\right)=\left({a}+\mathrm{2}{b}\right)^{\mathrm{2}} {r}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}\left({a}+\mathrm{2}{b}\right)\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){r} \\ $$$$\left({a}+\mathrm{2}{b}\right)^{\mathrm{2}} {r}^{\mathrm{2}} −\mathrm{2}\left[\mathrm{2}\left({a}^{\mathrm{3}} −{b}^{\mathrm{3}} \right)+{ab}\left(\mathrm{2}{a}−\mathrm{3}{b}\right)\right]{r}+{b}^{\mathrm{4}} =\mathrm{0} \\ $$$$\Rightarrow{r}=\frac{\mathrm{2}\left({a}^{\mathrm{3}} −{b}^{\mathrm{3}} \right)+{ab}\left(\mathrm{2}{a}−\mathrm{3}{b}\right)+\sqrt{\left[\mathrm{2}\left({a}^{\mathrm{3}} −{b}^{\mathrm{3}} \right)+{ab}\left(\mathrm{2}{a}−\mathrm{3}{b}\right)\right]^{\mathrm{2}} −\left({a}+\mathrm{2}{b}\right)^{\mathrm{2}} {b}^{\mathrm{4}} }}{\left({a}+\mathrm{2}{b}\right)^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 12/Jul/19
$$\mathcal{NICE}\:{n}\:\mathcal{WISE}\:{Sir},\:{Thank}\:{you}. \\ $$
