Question Number 63985 by Tawa1 last updated on 11/Jul/19
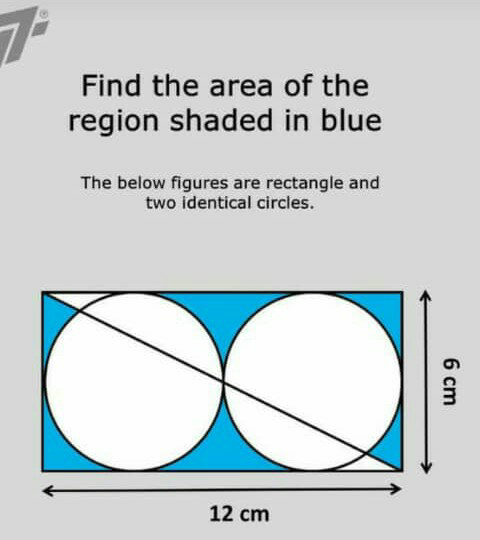
Answered by mr W last updated on 12/Jul/19
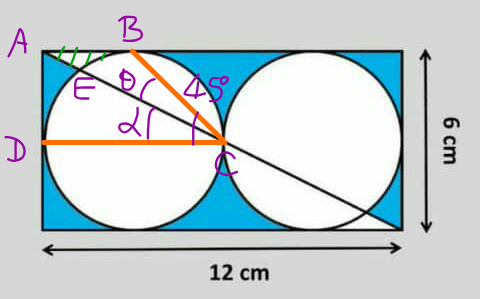
Commented by mr W last updated on 12/Jul/19
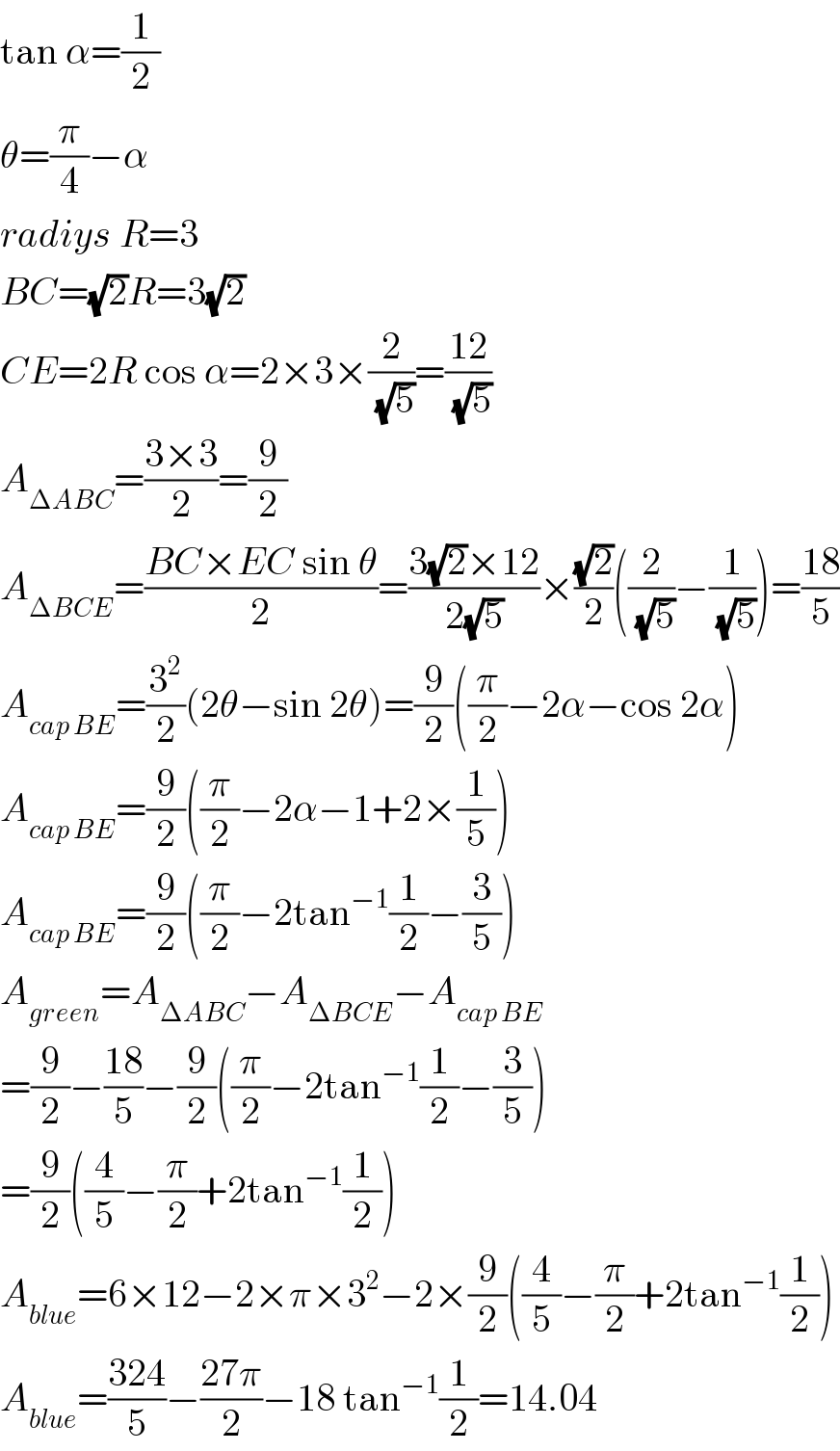
$$\mathrm{tan}\:\alpha=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\theta=\frac{\pi}{\mathrm{4}}−\alpha \\ $$$${radiys}\:{R}=\mathrm{3} \\ $$$${BC}=\sqrt{\mathrm{2}}{R}=\mathrm{3}\sqrt{\mathrm{2}} \\ $$$${CE}=\mathrm{2}{R}\:\mathrm{cos}\:\alpha=\mathrm{2}×\mathrm{3}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}=\frac{\mathrm{12}}{\:\sqrt{\mathrm{5}}} \\ $$$${A}_{\Delta{ABC}} =\frac{\mathrm{3}×\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{9}}{\mathrm{2}} \\ $$$${A}_{\Delta{BCE}} =\frac{{BC}×{EC}\:\mathrm{sin}\:\theta}{\mathrm{2}}=\frac{\mathrm{3}\sqrt{\mathrm{2}}×\mathrm{12}}{\mathrm{2}\sqrt{\mathrm{5}}}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)=\frac{\mathrm{18}}{\mathrm{5}} \\ $$$${A}_{{cap}\:{BE}} =\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\theta−\mathrm{sin}\:\mathrm{2}\theta\right)=\frac{\mathrm{9}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{2}\alpha−\mathrm{cos}\:\mathrm{2}\alpha\right) \\ $$$${A}_{{cap}\:{BE}} =\frac{\mathrm{9}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{2}\alpha−\mathrm{1}+\mathrm{2}×\frac{\mathrm{1}}{\mathrm{5}}\right) \\ $$$${A}_{{cap}\:{BE}} =\frac{\mathrm{9}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{2tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{5}}\right) \\ $$$${A}_{{green}} ={A}_{\Delta{ABC}} −{A}_{\Delta{BCE}} −{A}_{{cap}\:{BE}} \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}−\frac{\mathrm{18}}{\mathrm{5}}−\frac{\mathrm{9}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{2tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{5}}\right) \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}\left(\frac{\mathrm{4}}{\mathrm{5}}−\frac{\pi}{\mathrm{2}}+\mathrm{2tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${A}_{{blue}} =\mathrm{6}×\mathrm{12}−\mathrm{2}×\pi×\mathrm{3}^{\mathrm{2}} −\mathrm{2}×\frac{\mathrm{9}}{\mathrm{2}}\left(\frac{\mathrm{4}}{\mathrm{5}}−\frac{\pi}{\mathrm{2}}+\mathrm{2tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${A}_{{blue}} =\frac{\mathrm{324}}{\mathrm{5}}−\frac{\mathrm{27}\pi}{\mathrm{2}}−\mathrm{18}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}=\mathrm{14}.\mathrm{04} \\ $$
Commented by Tawa1 last updated on 12/Jul/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 12/Jul/19
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort} \\ $$
