Menu Close

Question-64009

Tinku Tara 0 Comments
Pin




Question Number 64009 by ajfour last updated on 12/Jul/19
Commented by ajfour last updated on 12/Jul/19
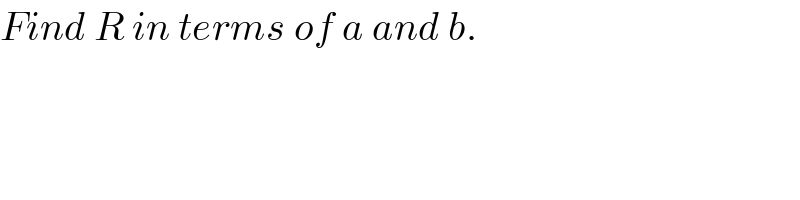
Find R in terms of a and b.
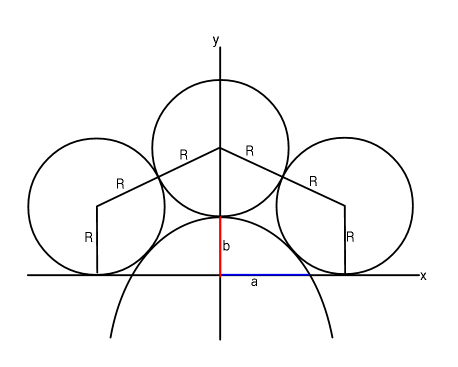
$${Find}\:{R}\:{in}\:{terms}\:{of}\:{a}\:{and}\:{b}. \\ $$
Answered by mr W last updated on 12/Jul/19
Commented by mr W last updated on 12/Jul/19
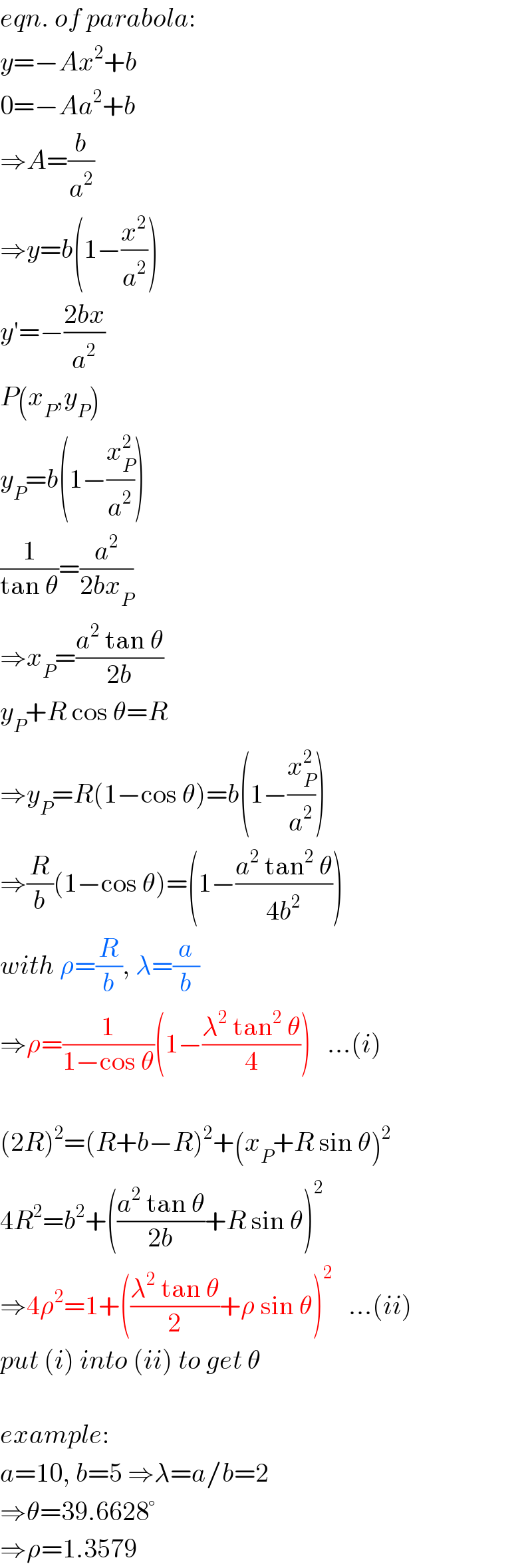
eqn. of parabola: y=−Ax^2 +b 0=−Aa^2 +b ⇒A=(b/a^2 ) ⇒y=b(1−(x^2 /a^2 )) y′=−((2bx)/a^2 ) P(x_P ,y_P ) y_P =b(1−(x_P ^2 /a^2 )) (1/(tan θ))=(a^2 /(2bx_P )) ⇒x_P =((a^2 tan θ)/(2b)) y_P +R cos θ=R ⇒y_P =R(1−cos θ)=b(1−(x_P ^2 /a^2 )) ⇒(R/b)(1−cos θ)=(1−((a^2 tan^2 θ)/(4b^2 ))) with ρ=(R/b), λ=(a/b) ⇒ρ=(1/(1−cos θ))(1−((λ^2 tan^2 θ)/4)) ...(i) (2R)^2 =(R+b−R)^2 +(x_P +R sin θ)^2 4R^2 =b^2 +(((a^2 tan θ)/(2b))+R sin θ)^2 ⇒4ρ^2 =1+(((λ^2 tan θ)/2)+ρ sin θ)^2 ...(ii) put (i) into (ii) to get θ example: a=10, b=5 ⇒λ=a/b=2 ⇒θ=39.6628° ⇒ρ=1.3579
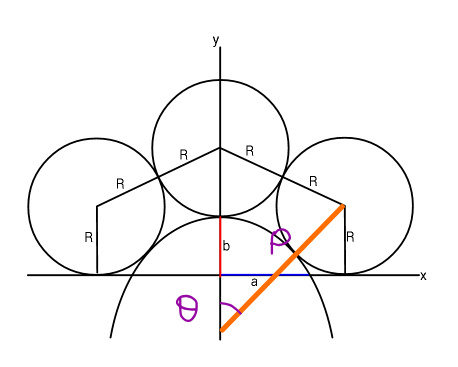
$${eqn}.\:{of}\:{parabola}: \\ $$$${y}=−{Ax}^{\mathrm{2}} +{b} \\ $$$$\mathrm{0}=−{Aa}^{\mathrm{2}} +{b} \\ $$$$\Rightarrow{A}=\frac{{b}}{{a}^{\mathrm{2}} } \\ $$$$\Rightarrow{y}={b}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right) \\ $$$${y}'=−\frac{\mathrm{2}{bx}}{{a}^{\mathrm{2}} } \\ $$$${P}\left({x}_{{P}} ,{y}_{{P}} \right) \\ $$$${y}_{{P}} ={b}\left(\mathrm{1}−\frac{{x}_{{P}} ^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\theta}=\frac{{a}^{\mathrm{2}} }{\mathrm{2}{bx}_{{P}} } \\ $$$$\Rightarrow{x}_{{P}} =\frac{{a}^{\mathrm{2}} \:\mathrm{tan}\:\theta}{\mathrm{2}{b}} \\ $$$${y}_{{P}} +{R}\:\mathrm{cos}\:\theta={R} \\ $$$$\Rightarrow{y}_{{P}} ={R}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)={b}\left(\mathrm{1}−\frac{{x}_{{P}} ^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\frac{{R}}{{b}}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)=\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} \:\mathrm{tan}^{\mathrm{2}} \:\theta}{\mathrm{4}{b}^{\mathrm{2}} }\right) \\ $$$${with}\:\rho=\frac{{R}}{{b}},\:\lambda=\frac{{a}}{{b}} \\ $$$$\Rightarrow\rho=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{cos}\:\theta}\left(\mathrm{1}−\frac{\lambda^{\mathrm{2}} \:\mathrm{tan}^{\mathrm{2}} \:\theta}{\mathrm{4}}\right)\:\:\:…\left({i}\right) \\ $$$$ \\ $$$$\left(\mathrm{2}{R}\right)^{\mathrm{2}} =\left({R}+{b}−{R}\right)^{\mathrm{2}} +\left({x}_{{P}} +{R}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$$\mathrm{4}{R}^{\mathrm{2}} ={b}^{\mathrm{2}} +\left(\frac{{a}^{\mathrm{2}} \:\mathrm{tan}\:\theta}{\mathrm{2}{b}}+{R}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4}\rho^{\mathrm{2}} =\mathrm{1}+\left(\frac{\lambda^{\mathrm{2}} \:\mathrm{tan}\:\theta}{\mathrm{2}}+\rho\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} \:\:\:…\left({ii}\right) \\ $$$${put}\:\left({i}\right)\:{into}\:\left({ii}\right)\:{to}\:{get}\:\theta \\ $$$$ \\ $$$${example}: \\ $$$${a}=\mathrm{10},\:{b}=\mathrm{5}\:\Rightarrow\lambda={a}/{b}=\mathrm{2} \\ $$$$\Rightarrow\theta=\mathrm{39}.\mathrm{6628}° \\ $$$$\Rightarrow\rho=\mathrm{1}.\mathrm{3579} \\ $$
Commented by mr W last updated on 12/Jul/19
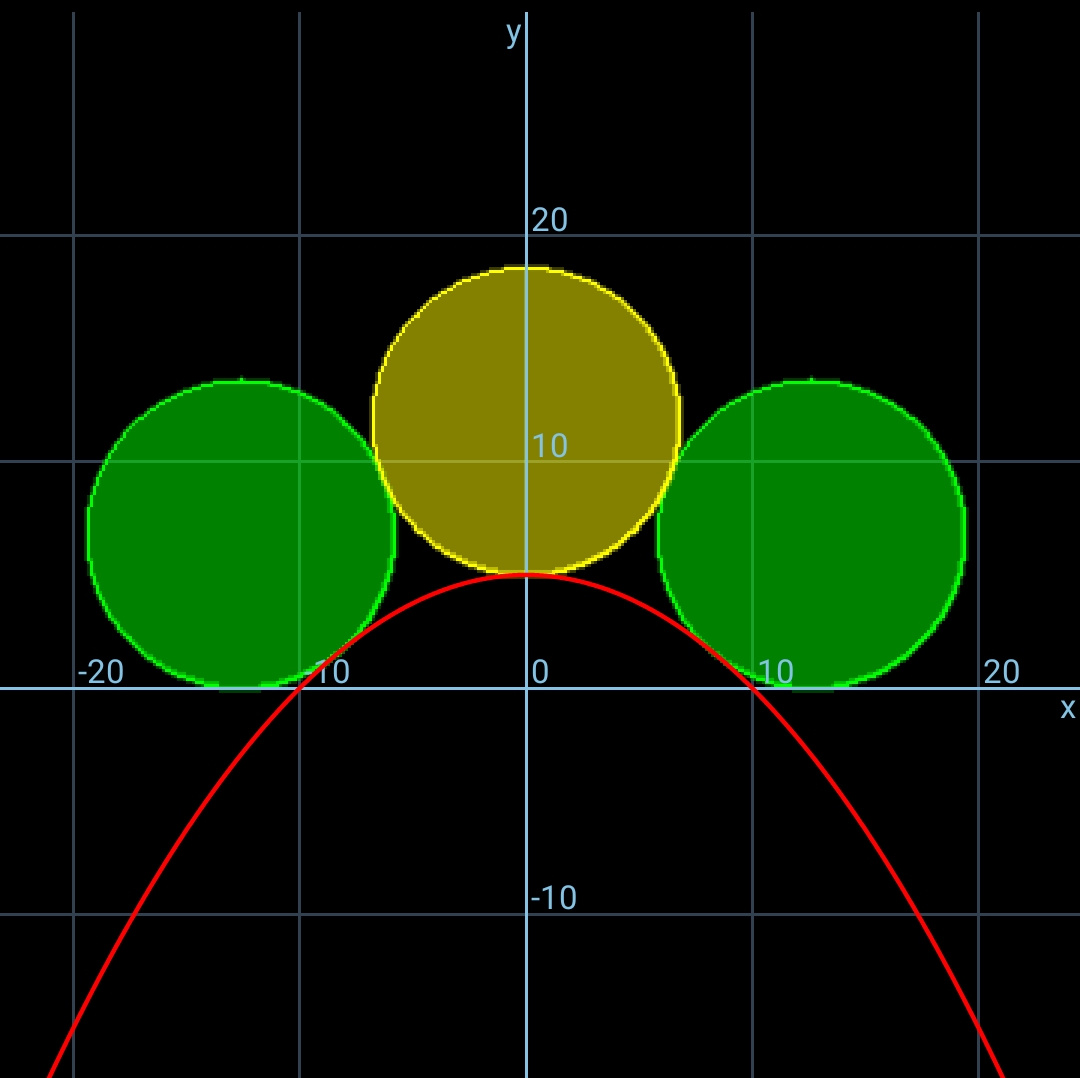
Commented by ajfour last updated on 12/Jul/19
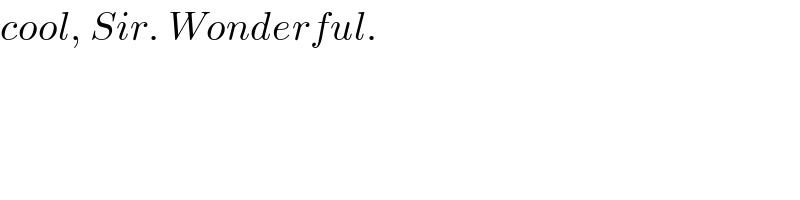
cool, Sir. Wonderful.
$${cool},\:{Sir}.\:{Wonderful}. \\ $$
Answered by ajfour last updated on 12/Jul/19
y=Ax^2 +b 0=Aa^2 +b ⇒ A=−b/a^2 let parabola touch the circle on right at (h,k). k=b(1−(h^2 /a^2 )) (dy/dx)=2Ax = 2(−(b/a^2 ))h slope of normal tan θ=(a^2 /(2bh)) let centre of right circle be C(p,q) p=h+Rcos θ , q=k+Rsin θ Now q=R and p^2 +b^2 =4R^2 ⇒ R=b(1−(h^2 /a^2 ))+Rsin θ (h+Rcos θ)^2 +b^2 =4R^2 tan θ=(a^2 /(2bh)) ⇒ h=((a^2 cos θ)/(2bsin θ)) ⇒ R=b(1−((a^2 cos^2 θ)/(4b^2 sin^2 θ)))+Rsin θ ⇒ R=(b/((1−sin θ)))(1−((a^2 cos^2 θ)/(4b^2 sin^2 θ))) (((a^2 cos θ)/(2bsin θ))+Rcos θ)^2 =4R^2 −b^2 [((a^2 cos θ)/(2bsin θ))+((b(1−((a^2 cos^2 θ)/(4b^2 sin^2 θ)))cos θ)/(1−sin θ))]^2 =[((2b(1−((a^2 cos^2 θ)/(4b^2 sin^2 θ))))/(1−sin θ))]^2 −b^2 let sin θ=t ⇒ (1−t^2 )[(a^2 /(2bt))+(b/(1−t))(1−((a^2 (1−t^2 ))/(4b^2 t^2 )))]^2 =[((2b(1−((a^2 (1−t^2 ))/(4b^2 t^2 ))))/(1−t))]^2 −b^2 ⇒ (1−t^2 )[2a^2 b(1−t)t+b{4b^2 t^2 −a^2 +a^2 t^2 }]^2 +16b^6 (1−t)^2 t^4 = 4b^2 [4b^2 t^2 −a^2 +a^2 t^2 ]^2 ⇒ (1−t^2 )[(4b^2 −a^2 )t^2 +2a^2 t−a^2 ]^2 +16b^4 (1−t)^2 t^4 =4[(a^2 +4b^2 )t^2 −a^2 ]^2 And for a=2, b=1 (1−t^2 )(2t−1)^2 =(1−t)^2 t^4 +4(2t^2 −1)^2 ⇒ t=0.7698144 R=(b/((1−sin θ)))(1−((a^2 cos^2 θ)/(4b^2 sin^2 θ))) R=((2t^2 −1)/(t^2 (1−t))) = 1.35787 ■
$${y}={Ax}^{\mathrm{2}} +{b} \\ $$$$\mathrm{0}={Aa}^{\mathrm{2}} +{b}\:\:\:\:\Rightarrow\:\:{A}=−{b}/{a}^{\mathrm{2}} \\ $$$${let}\:{parabola}\:{touch}\:{the}\:{circle}\:{on} \\ $$$${right}\:{at}\:\left({h},{k}\right). \\ $$$${k}={b}\left(\mathrm{1}−\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right) \\ $$$$\frac{{dy}}{{dx}}=\mathrm{2}{Ax}\:=\:\mathrm{2}\left(−\frac{{b}}{{a}^{\mathrm{2}} }\right){h} \\ $$$${slope}\:{of}\:{normal}\:\mathrm{tan}\:\theta=\frac{{a}^{\mathrm{2}} }{\mathrm{2}{bh}} \\ $$$${let}\:{centre}\:{of}\:{right}\:{circle}\:{be} \\ $$$${C}\left({p},{q}\right) \\ $$$$\:\:\:{p}={h}+{R}\mathrm{cos}\:\theta\:\:,\:{q}={k}+{R}\mathrm{sin}\:\theta \\ $$$${Now}\:\:\:{q}={R}\:\:{and} \\ $$$$\:\:\:{p}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{4}{R}^{\mathrm{2}} \\ $$$$\Rightarrow\:{R}={b}\left(\mathrm{1}−\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)+{R}\mathrm{sin}\:\theta \\ $$$$\:\:\:\left({h}+{R}\mathrm{cos}\:\theta\right)^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{4}{R}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\mathrm{tan}\:\theta=\frac{{a}^{\mathrm{2}} }{\mathrm{2}{bh}}\:\:\:\:\:\Rightarrow\:\:{h}=\frac{{a}^{\mathrm{2}} \mathrm{cos}\:\theta}{\mathrm{2}{b}\mathrm{sin}\:\theta} \\ $$$$ \\ $$$$\Rightarrow\:{R}={b}\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{4}{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}\right)+{R}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:\:{R}=\frac{{b}}{\left(\mathrm{1}−\mathrm{sin}\:\theta\right)}\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{4}{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}\right) \\ $$$$\left(\frac{{a}^{\mathrm{2}} \mathrm{cos}\:\theta}{\mathrm{2}{b}\mathrm{sin}\:\theta}+{R}\mathrm{cos}\:\theta\right)^{\mathrm{2}} =\mathrm{4}{R}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$$\left[\frac{{a}^{\mathrm{2}} \mathrm{cos}\:\theta}{\mathrm{2}{b}\mathrm{sin}\:\theta}+\frac{{b}\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{4}{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}\right)\mathrm{cos}\:\theta}{\mathrm{1}−\mathrm{sin}\:\theta}\right]^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left[\frac{\mathrm{2}{b}\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{4}{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}\right)}{\mathrm{1}−\mathrm{sin}\:\theta}\right]^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$${let}\:\:\mathrm{sin}\:\theta={t} \\ $$$$\Rightarrow\:\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left[\frac{{a}^{\mathrm{2}} }{\mathrm{2}{bt}}+\frac{{b}}{\mathrm{1}−{t}}\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{\mathrm{4}{b}^{\mathrm{2}} {t}^{\mathrm{2}} }\right)\right]^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:=\left[\frac{\mathrm{2}{b}\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{\mathrm{4}{b}^{\mathrm{2}} {t}^{\mathrm{2}} }\right)}{\mathrm{1}−{t}}\right]^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left[\mathrm{2}{a}^{\mathrm{2}} {b}\left(\mathrm{1}−{t}\right){t}+{b}\left\{\mathrm{4}{b}^{\mathrm{2}} {t}^{\mathrm{2}} −{a}^{\mathrm{2}} +{a}^{\mathrm{2}} {t}^{\mathrm{2}} \right\}\right]^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:+\mathrm{16}{b}^{\mathrm{6}} \left(\mathrm{1}−{t}\right)^{\mathrm{2}} {t}^{\mathrm{4}} \\ $$$$\:\:\:\:\:\:=\:\mathrm{4}{b}^{\mathrm{2}} \left[\mathrm{4}{b}^{\mathrm{2}} {t}^{\mathrm{2}} −{a}^{\mathrm{2}} +{a}^{\mathrm{2}} {t}^{\mathrm{2}} \right]^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\:\:\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left[\left(\mathrm{4}{b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right){t}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} {t}−{a}^{\mathrm{2}} \right]^{\mathrm{2}} \\ $$$$\:+\mathrm{16}{b}^{\mathrm{4}} \left(\mathrm{1}−{t}\right)^{\mathrm{2}} {t}^{\mathrm{4}} =\mathrm{4}\left[\left({a}^{\mathrm{2}} +\mathrm{4}{b}^{\mathrm{2}} \right){t}^{\mathrm{2}} −{a}^{\mathrm{2}} \right]^{\mathrm{2}} \\ $$$${And}\:{for}\:{a}=\mathrm{2},\:{b}=\mathrm{1} \\ $$$$\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{1}−{t}\right)^{\mathrm{2}} {t}^{\mathrm{4}} +\mathrm{4}\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:{t}=\mathrm{0}.\mathrm{7698144} \\ $$$${R}=\frac{{b}}{\left(\mathrm{1}−\mathrm{sin}\:\theta\right)}\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{4}{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}\right) \\ $$$$\:\:\:\:\:\:{R}=\frac{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} \left(\mathrm{1}−{t}\right)}\:=\:\mathrm{1}.\mathrm{35787}\:\blacksquare \\ $$
Commented by mr W last updated on 13/Jul/19
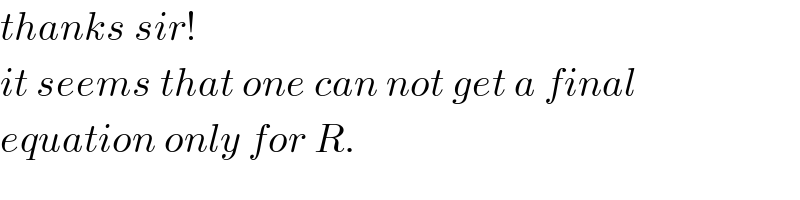
thanks sir! it seems that one can not get a final equation only for R.
$${thanks}\:{sir}! \\ $$$${it}\:{seems}\:{that}\:{one}\:{can}\:{not}\:{get}\:{a}\:{final} \\ $$$${equation}\:{only}\:{for}\:{R}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *