Question Number 64012 by aditya@345 last updated on 12/Jul/19

Answered by MJS last updated on 12/Jul/19
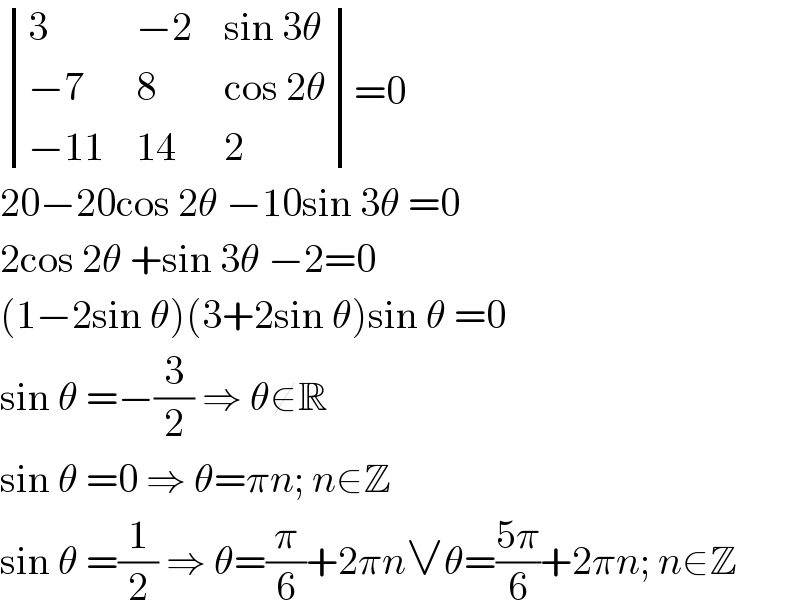
$$\begin{vmatrix}{\mathrm{3}}&{−\mathrm{2}}&{\mathrm{sin}\:\mathrm{3}\theta}\\{−\mathrm{7}}&{\mathrm{8}}&{\mathrm{cos}\:\mathrm{2}\theta}\\{−\mathrm{11}}&{\mathrm{14}}&{\mathrm{2}}\end{vmatrix}=\mathrm{0} \\ $$$$\mathrm{20}−\mathrm{20cos}\:\mathrm{2}\theta\:−\mathrm{10sin}\:\mathrm{3}\theta\:=\mathrm{0} \\ $$$$\mathrm{2cos}\:\mathrm{2}\theta\:+\mathrm{sin}\:\mathrm{3}\theta\:−\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{1}−\mathrm{2sin}\:\theta\right)\left(\mathrm{3}+\mathrm{2sin}\:\theta\right)\mathrm{sin}\:\theta\:=\mathrm{0} \\ $$$$\mathrm{sin}\:\theta\:=−\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow\:\theta\notin\mathbb{R} \\ $$$$\mathrm{sin}\:\theta\:=\mathrm{0}\:\Rightarrow\:\theta=\pi{n};\:{n}\in\mathbb{Z} \\ $$$$\mathrm{sin}\:\theta\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:\theta=\frac{\pi}{\mathrm{6}}+\mathrm{2}\pi{n}\vee\theta=\frac{\mathrm{5}\pi}{\mathrm{6}}+\mathrm{2}\pi{n};\:{n}\in\mathbb{Z} \\ $$
