Question Number 64097 by ajfour last updated on 13/Jul/19
Commented by ajfour last updated on 13/Jul/19
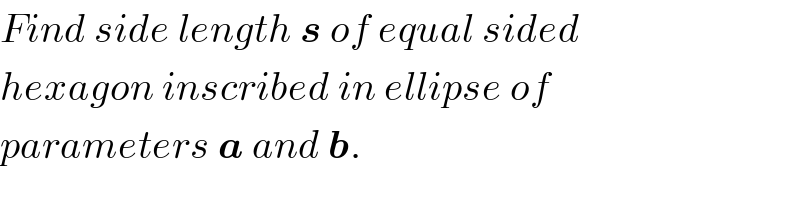
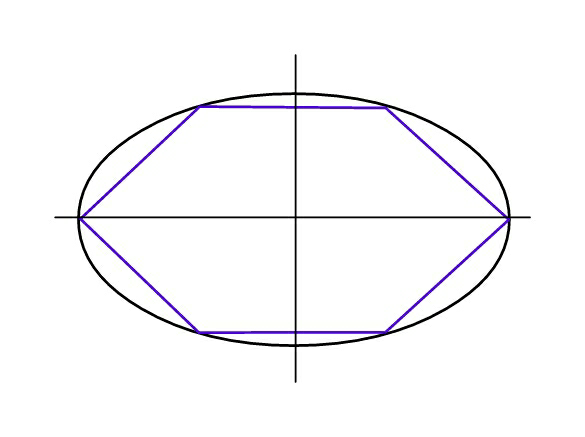
$${Find}\:{side}\:{length}\:\boldsymbol{{s}}\:{of}\:{equal}\:{sided} \\ $$$${hexagon}\:{inscribed}\:{in}\:{ellipse}\:{of} \\ $$$${parameters}\:\boldsymbol{{a}}\:{and}\:\boldsymbol{{b}}. \\ $$
Answered by ajfour last updated on 13/Jul/19
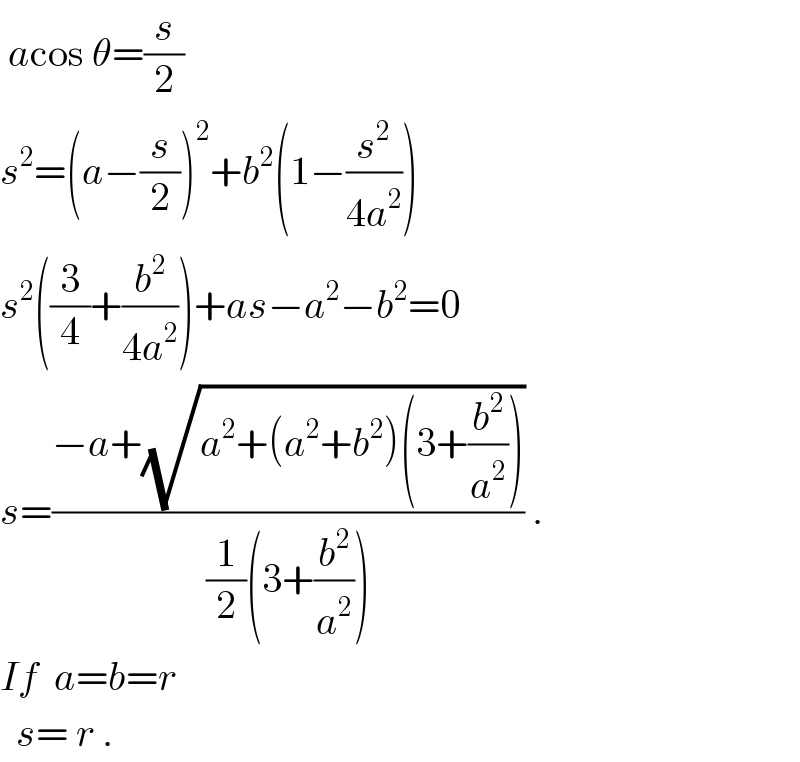
$$\:{a}\mathrm{cos}\:\theta=\frac{{s}}{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} =\left({a}−\frac{{s}}{\mathrm{2}}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} \left(\mathrm{1}−\frac{{s}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }\right) \\ $$$${s}^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}+\frac{{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }\right)+{as}−{a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{0} \\ $$$${s}=\frac{−{a}+\sqrt{{a}^{\mathrm{2}} +\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left(\mathrm{3}+\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)}}{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}+\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)}\:. \\ $$$${If}\:\:{a}={b}={r} \\ $$$$\:\:{s}=\:{r}\:. \\ $$
Commented by mr W last updated on 13/Jul/19
��
