Question Number 64112 by mr W last updated on 13/Jul/19

Commented by mr W last updated on 13/Jul/19
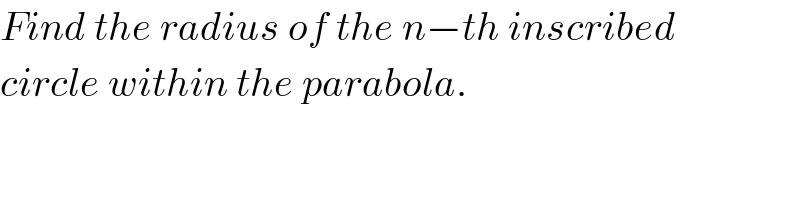
$${Find}\:{the}\:{radius}\:{of}\:{the}\:{n}−{th}\:{inscribed} \\ $$$${circle}\:{within}\:{the}\:{parabola}. \\ $$
Answered by ajfour last updated on 13/Jul/19
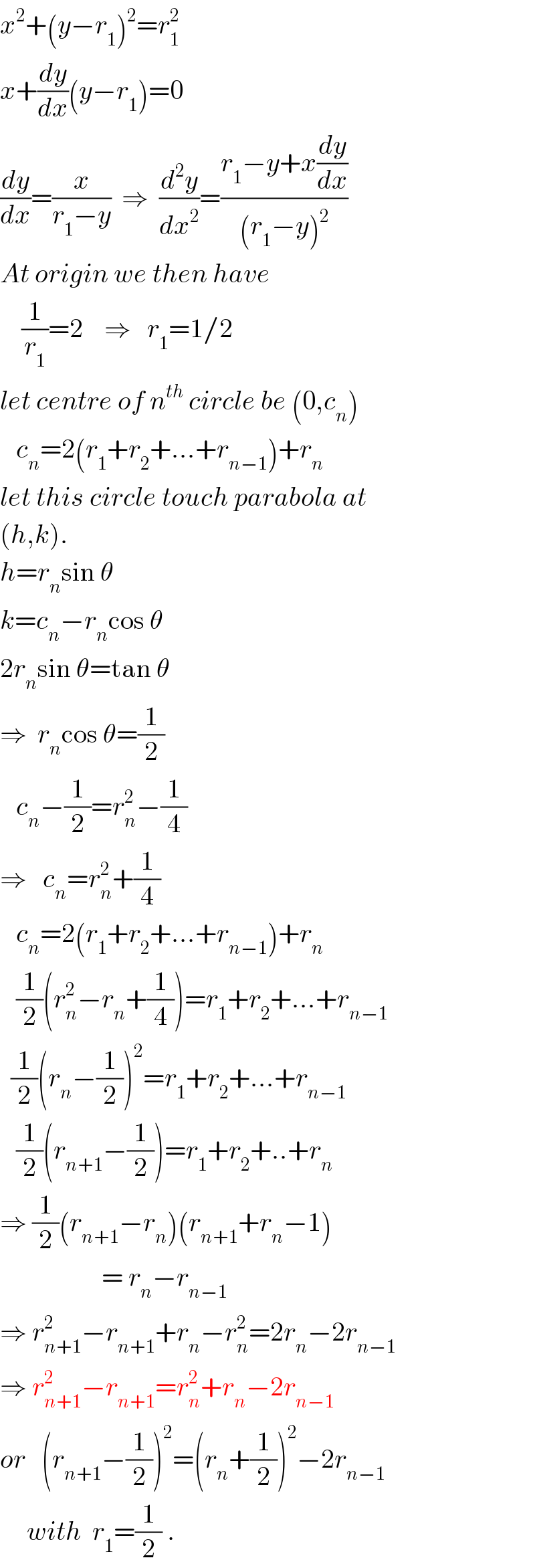
$${x}^{\mathrm{2}} +\left({y}−{r}_{\mathrm{1}} \right)^{\mathrm{2}} ={r}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$${x}+\frac{{dy}}{{dx}}\left({y}−{r}_{\mathrm{1}} \right)=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}=\frac{{x}}{{r}_{\mathrm{1}} −{y}}\:\:\Rightarrow\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{r}_{\mathrm{1}} −{y}+{x}\frac{{dy}}{{dx}}}{\left({r}_{\mathrm{1}} −{y}\right)^{\mathrm{2}} } \\ $$$${At}\:{origin}\:{we}\:{then}\:{have} \\ $$$$\:\:\:\:\frac{\mathrm{1}}{{r}_{\mathrm{1}} }=\mathrm{2}\:\:\:\:\Rightarrow\:\:\:{r}_{\mathrm{1}} =\mathrm{1}/\mathrm{2} \\ $$$${let}\:{centre}\:{of}\:{n}^{{th}} \:{circle}\:{be}\:\left(\mathrm{0},{c}_{{n}} \right) \\ $$$$\:\:\:{c}_{{n}} =\mathrm{2}\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} +…+{r}_{{n}−\mathrm{1}} \right)+{r}_{{n}} \\ $$$${let}\:{this}\:{circle}\:{touch}\:{parabola}\:{at} \\ $$$$\left({h},{k}\right). \\ $$$${h}={r}_{{n}} \mathrm{sin}\:\theta \\ $$$${k}={c}_{{n}} −{r}_{{n}} \mathrm{cos}\:\theta \\ $$$$\mathrm{2}{r}_{{n}} \mathrm{sin}\:\theta=\mathrm{tan}\:\theta \\ $$$$\Rightarrow\:\:{r}_{{n}} \mathrm{cos}\:\theta=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:{c}_{{n}} −\frac{\mathrm{1}}{\mathrm{2}}={r}_{{n}} ^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\:\:\:{c}_{{n}} ={r}_{{n}} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\:\:\:{c}_{{n}} =\mathrm{2}\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} +…+{r}_{{n}−\mathrm{1}} \right)+{r}_{{n}} \\ $$$$\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\left({r}_{{n}} ^{\mathrm{2}} −{r}_{{n}} +\frac{\mathrm{1}}{\mathrm{4}}\right)={r}_{\mathrm{1}} +{r}_{\mathrm{2}} +…+{r}_{{n}−\mathrm{1}} \\ $$$$\:\:\frac{\mathrm{1}}{\mathrm{2}}\left({r}_{{n}} −\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} ={r}_{\mathrm{1}} +{r}_{\mathrm{2}} +…+{r}_{{n}−\mathrm{1}} \\ $$$$\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\left({r}_{{n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\right)={r}_{\mathrm{1}} +{r}_{\mathrm{2}} +..+{r}_{{n}} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\left({r}_{{n}+\mathrm{1}} −{r}_{{n}} \right)\left({r}_{{n}+\mathrm{1}} +{r}_{{n}} −\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{r}_{{n}} −{r}_{{n}−\mathrm{1}} \\ $$$$\Rightarrow\:{r}_{{n}+\mathrm{1}} ^{\mathrm{2}} −{r}_{{n}+\mathrm{1}} +{r}_{{n}} −{r}_{{n}} ^{\mathrm{2}} =\mathrm{2}{r}_{{n}} −\mathrm{2}{r}_{{n}−\mathrm{1}} \\ $$$$\Rightarrow\:{r}_{{n}+\mathrm{1}} ^{\mathrm{2}} −{r}_{{n}+\mathrm{1}} ={r}_{{n}} ^{\mathrm{2}} +{r}_{{n}} −\mathrm{2}{r}_{{n}−\mathrm{1}} \\ $$$${or}\:\:\:\left({r}_{{n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\left({r}_{{n}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{2}{r}_{{n}−\mathrm{1}} \\ $$$$\:\:\:\:\:{with}\:\:{r}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\:. \\ $$
Commented by mr W last updated on 13/Jul/19

$${thank}\:{you}\:{sir}!\: \\ $$$${acc}.\:{to}\:{drawing}\:{it}\:{seems}\:{that} \\ $$$${r}_{{n}} ={n}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${but}\:{this}\:{doesn}'{t}\:{match}\: \\ $$$$\left({r}_{{n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\left({r}_{{n}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{2}{r}_{{n}−\mathrm{1}} \\ $$$${can}\:{you}\:{please}\:{recheck}? \\ $$
Answered by mr W last updated on 13/Jul/19
![first circle touches the parabola at (0,0) y′=2x y′′=2 ⇒R=(1/2) ⇒radius of the first circle r_1 =(1/2) let r_n =radius of nth circle d_n =diameter of nth circle, d_n =2r_n the nth circle touches the n−1th circle at (0,d_1 +d_2 +...d_(n−1) ) let a_n =d_1 +d_2 +...d_(n−1) =2(r_1 +r_2 +...+r_(n−1) ) eqn. of nth circle: x^2 +(y−a_n −r_n )^2 =r_n ^2 intersection with parabola y=x^2 : y+(y−a_n −r_n )^2 =r_n ^2 ⇒y^2 −[2(a_n +r_n )−1]y+a_n (a_n +2r_n )=0 due to tangency: Δ=[2(a_n +r_n )−1]^2 −4a_n (a_n +2r_n )=0 4(a_n ^2 +2a_n r_n +r_n ^2 )−4(a_n +r_n )+1−4a_n ^2 −8a_n r_n =0 r_n ^2 −r_n −(a_n −(1/4))=0 ⇒r_n =(1/2)+(√a_n ) ⇒r_n =(1/2)+(√(2(r_1 +r_2 +...+r_(n−1) ))) (r_n −(1/2))^2 =2(r_1 +r_2 +...+r_(n−1) ) ⇒r_n ^2 −r_n +(1/4)=2(r_1 +r_2 +...+r_(n−1) ) ...(i) ⇒r_(n−1) ^2 −r_(n−1) +(1/4)=2(r_1 +r_2 +...+r_(n−2) ) ⇒r_(n−1) ^2 +r_(n−1) +(1/4)=2(r_1 +r_2 +...+r_(n−1) ) ...(ii) (i)−(ii): (r_n +r_(n−1) )(r_n −r_(n−1) −1)=0 ⇒r_n −r_(n−1) −1=0 ⇒r_n −r_(n−1) =1 ⇒r_1 ,r_2 ,r_3 ,..,r_n are A.P. with common difference 1, since r_1 =(1/2), ⇒r_n =(1/2)+(n−1)×1=n−(1/2)](https://www.tinkutara.com/question/Q64117.png)
$${first}\:{circle}\:{touches}\:{the}\:{parabola}\:{at}\:\left(\mathrm{0},\mathrm{0}\right) \\ $$$${y}'=\mathrm{2}{x} \\ $$$${y}''=\mathrm{2}\:\Rightarrow{R}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{radius}\:{of}\:{the}\:{first}\:{circle}\:{r}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${let}\:{r}_{{n}} ={radius}\:{of}\:{nth}\:{circle} \\ $$$${d}_{{n}} ={diameter}\:{of}\:{nth}\:{circle},\:{d}_{{n}} =\mathrm{2}{r}_{{n}} \\ $$$${the}\:{nth}\:{circle}\:{touches}\:{the}\:{n}−\mathrm{1}{th}\:{circle} \\ $$$${at}\:\left(\mathrm{0},{d}_{\mathrm{1}} +{d}_{\mathrm{2}} +…{d}_{{n}−\mathrm{1}} \right) \\ $$$${let}\:{a}_{{n}} ={d}_{\mathrm{1}} +{d}_{\mathrm{2}} +…{d}_{{n}−\mathrm{1}} =\mathrm{2}\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} +…+{r}_{{n}−\mathrm{1}} \right) \\ $$$${eqn}.\:{of}\:{nth}\:{circle}: \\ $$$${x}^{\mathrm{2}} +\left({y}−{a}_{{n}} −{r}_{{n}} \right)^{\mathrm{2}} ={r}_{{n}} ^{\mathrm{2}} \\ $$$${intersection}\:{with}\:{parabola}\:{y}={x}^{\mathrm{2}} : \\ $$$${y}+\left({y}−{a}_{{n}} −{r}_{{n}} \right)^{\mathrm{2}} ={r}_{{n}} ^{\mathrm{2}} \\ $$$$\Rightarrow{y}^{\mathrm{2}} −\left[\mathrm{2}\left({a}_{{n}} +{r}_{{n}} \right)−\mathrm{1}\right]{y}+{a}_{{n}} \left({a}_{{n}} +\mathrm{2}{r}_{{n}} \right)=\mathrm{0} \\ $$$${due}\:{to}\:{tangency}: \\ $$$$\Delta=\left[\mathrm{2}\left({a}_{{n}} +{r}_{{n}} \right)−\mathrm{1}\right]^{\mathrm{2}} −\mathrm{4}{a}_{{n}} \left({a}_{{n}} +\mathrm{2}{r}_{{n}} \right)=\mathrm{0} \\ $$$$\mathrm{4}\left({a}_{{n}} ^{\mathrm{2}} +\mathrm{2}{a}_{{n}} {r}_{{n}} +{r}_{{n}} ^{\mathrm{2}} \right)−\mathrm{4}\left({a}_{{n}} +{r}_{{n}} \right)+\mathrm{1}−\mathrm{4}{a}_{{n}} ^{\mathrm{2}} −\mathrm{8}{a}_{{n}} {r}_{{n}} =\mathrm{0} \\ $$$${r}_{{n}} ^{\mathrm{2}} −{r}_{{n}} −\left({a}_{{n}} −\frac{\mathrm{1}}{\mathrm{4}}\right)=\mathrm{0} \\ $$$$\Rightarrow{r}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{{a}_{{n}} } \\ $$$$\Rightarrow{r}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{2}\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} +…+{r}_{{n}−\mathrm{1}} \right)} \\ $$$$\left({r}_{{n}} −\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{2}\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} +…+{r}_{{n}−\mathrm{1}} \right) \\ $$$$\Rightarrow{r}_{{n}} ^{\mathrm{2}} −{r}_{{n}} +\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{2}\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} +…+{r}_{{n}−\mathrm{1}} \right)\:\:\:…\left({i}\right) \\ $$$$\Rightarrow{r}_{{n}−\mathrm{1}} ^{\mathrm{2}} −{r}_{{n}−\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{2}\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} +…+{r}_{{n}−\mathrm{2}} \right) \\ $$$$\Rightarrow{r}_{{n}−\mathrm{1}} ^{\mathrm{2}} +{r}_{{n}−\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{2}\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} +…+{r}_{{n}−\mathrm{1}} \right)\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\left({r}_{{n}} +{r}_{{n}−\mathrm{1}} \right)\left({r}_{{n}} −{r}_{{n}−\mathrm{1}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{r}_{{n}} −{r}_{{n}−\mathrm{1}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{r}_{{n}} −{r}_{{n}−\mathrm{1}} =\mathrm{1} \\ $$$$\Rightarrow{r}_{\mathrm{1}} ,{r}_{\mathrm{2}} ,{r}_{\mathrm{3}} ,..,{r}_{{n}} \:{are}\:{A}.{P}.\:{with}\:{common} \\ $$$${difference}\:\mathrm{1},\:{since}\:{r}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}, \\ $$$$\Rightarrow{r}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}+\left({n}−\mathrm{1}\right)×\mathrm{1}={n}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by ajfour last updated on 13/Jul/19
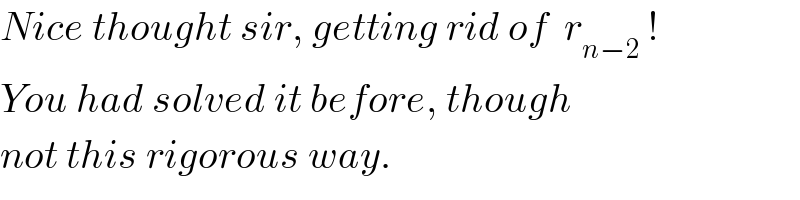
$${Nice}\:{thought}\:{sir},\:{getting}\:{rid}\:{of}\:\:{r}_{{n}−\mathrm{2}} \:! \\ $$$${You}\:{had}\:{solved}\:{it}\:{before},\:{though} \\ $$$${not}\:{this}\:{rigorous}\:{way}. \\ $$
Commented by mr W last updated on 13/Jul/19

$${to}\:{be}\:{honest}\:{i}\:{found}\:{at}\:{first}\:{only}\:{the} \\ $$$${relation}\:{r}=\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{{a}}\:{and}\:{drew}\:{the}\:{circles} \\ $$$${one}\:{after}\:{one}.\:{after}\:{i}\:{have}\:{posted}\:{the}\:{question}, \\ $$$${i}\:{found}\:{that}\:{the}\:{circles}\:{touch}\:{each}\:{other}\: \\ $$$${always}\:{at}\:{perfect}\:{squares}\:\mathrm{1},\:\mathrm{4},\:\mathrm{9},\:\mathrm{16}… \\ $$$${that}\:{means}\:{the}\:{radii}\:{are}\:{an}\:{A}.{P}. \\ $$$${after}\:{i}\:{have}\:{read}\:{your}\:{post}\:{i}\:{tried}\:{to}\:{find} \\ $$$${a}\:{way}\:{to}\:{prove}\:{this}.\:{i}\:{found}\:{a}\:{way}\:{after}\: \\ $$$${some}\:{trials}. \\ $$
Commented by Tawa11 last updated on 04/Jan/22

$$\mathrm{I}\:\mathrm{just}\:\mathrm{see}\:\mathrm{this}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
