Question Number 64119 by ajfour last updated on 13/Jul/19

Commented by ajfour last updated on 13/Jul/19

$${In}\:{terms}\:{of}\:{the}\:{sides}\:{of}\:\bigtriangleup{ABC},\:{find} \\ $$$${the}\:{radius}\:{of}\:{the}\:{central}\:{circle}. \\ $$
Answered by ajfour last updated on 14/Jul/19
![p :radius of circle with center A q : center B ; r : center C and R : radius of central circle q+r=a r+p=b p+q=c p+q+r=s p=s−a , q=s−b , r=s−c let center of small circle be (0,k_A ) (x+q)^2 +y^2 =(q+R)^2 (x−r)^2 +y^2 =(r+R)^2 ⇒ (2x+q−r)(q+r)=(q−r)(q+r+2R) ⇒ 2x=(((q−r)(q+r+2R))/(q+r))−(q−r) x=(((q−r)R)/(q+r)) y^2 =(q+R)^2 −(q+(((q−r)R)/(q+r)))^2 y^2 =[q+R+q+(((q−r)R)/(q+r))][R−(((q−r)R)/(q+r))] y^2 =((4qrR)/(q+r))[1+(R/(q+r))] k_A =(√(((4qrR)/(q+r))(1+(R/(q+r))))) ⇒ k_A =(2/a)(√(qrR(a+R))) let Area of △ABC be △. △=((ak_A +bk_B +ck_C )/2) ⇒ (√(qrR(a+R)))+(√(rpR(b+R)))+ +(√(pqR(c+R))) = △ ....](https://www.tinkutara.com/question/Q64131.png)
$${p}\::{radius}\:{of}\:{circle}\:{with}\:{center}\:{A} \\ $$$${q}\::\:\:{center}\:{B}\:; \\ $$$${r}\::\:{center}\:{C} \\ $$$${and}\:{R}\::\:{radius}\:{of}\:{central}\:{circle} \\ $$$${q}+{r}={a} \\ $$$${r}+{p}={b} \\ $$$${p}+{q}={c} \\ $$$${p}+{q}+{r}={s} \\ $$$${p}={s}−{a}\:,\:{q}={s}−{b}\:,\:{r}={s}−{c} \\ $$$${let}\:{center}\:{of}\:{small}\:{circle}\:{be}\:\left(\mathrm{0},{k}_{{A}} \right) \\ $$$$\left({x}+{q}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\left({q}+{R}\right)^{\mathrm{2}} \\ $$$$\left({x}−{r}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\left({r}+{R}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\left(\mathrm{2}{x}+{q}−{r}\right)\left({q}+{r}\right)=\left({q}−{r}\right)\left({q}+{r}+\mathrm{2}{R}\right) \\ $$$$\Rightarrow\:\mathrm{2}{x}=\frac{\left({q}−{r}\right)\left({q}+{r}+\mathrm{2}{R}\right)}{{q}+{r}}−\left({q}−{r}\right) \\ $$$$\:{x}=\frac{\left({q}−{r}\right){R}}{{q}+{r}} \\ $$$$\:{y}^{\mathrm{2}} =\left({q}+{R}\right)^{\mathrm{2}} −\left({q}+\frac{\left({q}−{r}\right){R}}{{q}+{r}}\right)^{\mathrm{2}} \\ $$$$\:{y}^{\mathrm{2}} =\left[{q}+{R}+{q}+\frac{\left({q}−{r}\right){R}}{{q}+{r}}\right]\left[{R}−\frac{\left({q}−{r}\right){R}}{{q}+{r}}\right] \\ $$$$\:{y}^{\mathrm{2}} =\frac{\mathrm{4}{qrR}}{{q}+{r}}\left[\mathrm{1}+\frac{{R}}{{q}+{r}}\right] \\ $$$${k}_{{A}} =\sqrt{\frac{\mathrm{4}{qrR}}{{q}+{r}}\left(\mathrm{1}+\frac{{R}}{{q}+{r}}\right)}\: \\ $$$$\Rightarrow\:\:\boldsymbol{{k}}_{\boldsymbol{{A}}} =\frac{\mathrm{2}}{{a}}\sqrt{{qrR}\left({a}+{R}\right)} \\ $$$${let}\:{Area}\:{of}\:\bigtriangleup{ABC}\:{be}\:\bigtriangleup. \\ $$$$\bigtriangleup=\frac{{ak}_{{A}} +{bk}_{{B}} +{ck}_{{C}} }{\mathrm{2}} \\ $$$$\Rightarrow\:\sqrt{{qrR}\left({a}+{R}\right)}+\sqrt{{rpR}\left({b}+{R}\right)}+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\sqrt{{pqR}\left({c}+{R}\right)}\:=\:\bigtriangleup \\ $$$$…. \\ $$
Answered by ajfour last updated on 15/Jul/19
![let center of central circle be (h,k) and radius ρ. let B be origin. h^2 +k^2 =(q+ρ)^2 (h−q−r)^2 +k^2 =(r+ρ)^2 ⇒(q+r)[2h−(q+r)]=(q−r)(q+r+2ρ) 2h=(((q−r)(2ρ+q+r))/(q+r))+q+r h =((ρ(q−r))/(q+r))+q k^2 =(q+ρ)^2 −[((ρ(q−r))/(q+r))+q]^2 k^2 =ρ^2 +2qρ−((ρ^2 (q−r)^2 )/((q+r)^2 ))−((2qρ(q−r))/(q+r)) =((4qrρ^2 )/((q+r)^2 ))+((4qrρ)/((q+r))) = ((4qrρ[ρ+(q+r)])/((q+r)^2 )) let A(x_A , y_A ) x_A =(p+q)cos B y_B =(p+q)sin B [h−(p+q)cos B]^2 +[k−(p+q)sin B]^2 =(p+ρ)^2 ⇒ (q+ρ)^2 +(p+q)^2 −(ρ+p)^2 = 2(p+q)[hcos B+ksin B] ⇒ [((q^2 +qρ+pq−pρ)/(p+q))−hcos B]^2 =k^2 sin^2 B ⇒ [((q^2 +qρ+pq−pρ)/(p+q))−(((ρ(q−r))/(q+r))+q)cos B]^2 =((4qrρ[ρ+(q+r)])/((q+r)^2 ))sin^2 B ⇒[((ρ(q−p))/c)−((ρ(q−r)cos B)/a)+q(1−cos B)]^2 =((4qrρ^2 )/a^2 )sin^2 B+((4qrρ)/a)sin^2 B ⇒ quadratic in ρ ; one is radius of circumcircle of the three circles, and the other the radius of required central one. ⇒ [(A−B)ρ+C]^2 =Dρ^2 +Eρ [(A−B)^2 −D]ρ^2 +[2C(A−B)−E]ρ+C^2 =0 ρ=((−2C(A−B)+E−(√(−4C(A−B)+E^2 +4C^2 D)))/(2[(A−B)^2 −D])) ρ =((−2q(1−cos B)[((q−p)/c)−(((q−r))/a)cos B]+((4qr)/a)sin^2 B−(√(−4q(1−cos B)[((q−p)/c)−(((q−r))/a)cos B]+((16q^2 r^2 )/a^2 )sin^4 B+4q^2 (1−cos B)^2 (((4qr)/a^2 )sin^2 B))))/(2[((q−p)/c)−(((q−r))/a)cos B]^2 −((8qr)/a^2 )sin^2 B)) with cos B = ((c^2 +a^2 −b^2 )/(2ac)) and p=s−a , q=s−b , r=s−c ■](https://www.tinkutara.com/question/Q64137.png)
$${let}\:{center}\:{of}\:{central}\:{circle}\:{be} \\ $$$$\:\:\left({h},{k}\right)\:{and}\:{radius}\:\rho. \\ $$$${let}\:{B}\:{be}\:{origin}. \\ $$$${h}^{\mathrm{2}} +{k}^{\mathrm{2}} =\left({q}+\rho\right)^{\mathrm{2}} \\ $$$$\left({h}−{q}−{r}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} =\left({r}+\rho\right)^{\mathrm{2}} \\ $$$$\Rightarrow\left({q}+{r}\right)\left[\mathrm{2}{h}−\left({q}+{r}\right)\right]=\left({q}−{r}\right)\left({q}+{r}+\mathrm{2}\rho\right) \\ $$$$\mathrm{2}{h}=\frac{\left({q}−{r}\right)\left(\mathrm{2}\rho+{q}+{r}\right)}{{q}+{r}}+{q}+{r} \\ $$$$\:\:\:\:{h}\:=\frac{\rho\left({q}−{r}\right)}{{q}+{r}}+{q} \\ $$$$\:\:\:\:{k}^{\mathrm{2}} =\left({q}+\rho\right)^{\mathrm{2}} −\left[\frac{\rho\left({q}−{r}\right)}{{q}+{r}}+{q}\right]^{\mathrm{2}} \\ $$$$\:\:\:\:{k}^{\mathrm{2}} =\rho^{\mathrm{2}} +\mathrm{2}{q}\rho−\frac{\rho^{\mathrm{2}} \left({q}−{r}\right)^{\mathrm{2}} }{\left({q}+{r}\right)^{\mathrm{2}} }−\frac{\mathrm{2}{q}\rho\left({q}−{r}\right)}{{q}+{r}} \\ $$$$\:\:\:=\frac{\mathrm{4}{qr}\rho^{\mathrm{2}} }{\left({q}+{r}\right)^{\mathrm{2}} }+\frac{\mathrm{4}{qr}\rho}{\left({q}+{r}\right)}\:=\:\frac{\mathrm{4}{qr}\rho\left[\rho+\left({q}+{r}\right)\right]}{\left({q}+{r}\right)^{\mathrm{2}} } \\ $$$${let}\:{A}\left({x}_{{A}} ,\:{y}_{{A}} \right) \\ $$$$\:\:\:{x}_{{A}} =\left({p}+{q}\right)\mathrm{cos}\:{B} \\ $$$$\:\:\:\:{y}_{{B}} =\left({p}+{q}\right)\mathrm{sin}\:{B} \\ $$$$\left[{h}−\left({p}+{q}\right)\mathrm{cos}\:{B}\right]^{\mathrm{2}} +\left[{k}−\left({p}+{q}\right)\mathrm{sin}\:{B}\right]^{\mathrm{2}} =\left({p}+\rho\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\left({q}+\rho\right)^{\mathrm{2}} +\left({p}+{q}\right)^{\mathrm{2}} −\left(\rho+{p}\right)^{\mathrm{2}} \\ $$$$\:\:\:=\:\mathrm{2}\left({p}+{q}\right)\left[{h}\mathrm{cos}\:{B}+{k}\mathrm{sin}\:{B}\right] \\ $$$$\Rightarrow\:\left[\frac{{q}^{\mathrm{2}} +{q}\rho+{pq}−{p}\rho}{{p}+{q}}−{h}\mathrm{cos}\:{B}\right]^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={k}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} {B} \\ $$$$\Rightarrow\:\:\left[\frac{{q}^{\mathrm{2}} +{q}\rho+{pq}−{p}\rho}{{p}+{q}}−\left(\frac{\rho\left({q}−{r}\right)}{{q}+{r}}+{q}\right)\mathrm{cos}\:{B}\right]^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{4}{qr}\rho\left[\rho+\left({q}+{r}\right)\right]}{\left({q}+{r}\right)^{\mathrm{2}} }\mathrm{sin}\:^{\mathrm{2}} {B} \\ $$$$\Rightarrow\left[\frac{\rho\left({q}−{p}\right)}{{c}}−\frac{\rho\left({q}−{r}\right)\mathrm{cos}\:{B}}{{a}}+{q}\left(\mathrm{1}−\mathrm{cos}\:{B}\right)\right]^{\mathrm{2}} \\ $$$$\:\:\:\:=\frac{\mathrm{4}{qr}\rho^{\mathrm{2}} }{{a}^{\mathrm{2}} }\mathrm{sin}\:^{\mathrm{2}} {B}+\frac{\mathrm{4}{qr}\rho}{{a}}\mathrm{sin}\:^{\mathrm{2}} {B} \\ $$$$\Rightarrow\:\:{quadratic}\:{in}\:\rho\:; \\ $$$$\:{one}\:{is}\:{radius}\:{of}\:{circumcircle} \\ $$$${of}\:{the}\:{three}\:{circles},\:{and}\:{the}\:{other} \\ $$$${the}\:{radius}\:{of}\:{required}\:{central}\:{one}. \\ $$$$\Rightarrow\:\left[\left({A}−{B}\right)\rho+{C}\right]^{\mathrm{2}} ={D}\rho^{\mathrm{2}} +{E}\rho \\ $$$$\:\:\:\left[\left({A}−{B}\right)^{\mathrm{2}} −{D}\right]\rho^{\mathrm{2}} +\left[\mathrm{2}{C}\left({A}−{B}\right)−{E}\right]\rho+{C}^{\mathrm{2}} =\mathrm{0} \\ $$$$\rho=\frac{−\mathrm{2}{C}\left({A}−{B}\right)+{E}−\sqrt{−\mathrm{4}{C}\left({A}−{B}\right)+{E}^{\mathrm{2}} +\mathrm{4}{C}^{\mathrm{2}} {D}}}{\mathrm{2}\left[\left({A}−{B}\right)^{\mathrm{2}} −{D}\right]} \\ $$$$\rho\:=\frac{−\mathrm{2}{q}\left(\mathrm{1}−\mathrm{cos}\:{B}\right)\left[\frac{{q}−{p}}{{c}}−\frac{\left({q}−{r}\right)}{{a}}\mathrm{cos}\:{B}\right]+\frac{\mathrm{4}{qr}}{{a}}\mathrm{sin}\:^{\mathrm{2}} {B}−\sqrt{−\mathrm{4}{q}\left(\mathrm{1}−\mathrm{cos}\:{B}\right)\left[\frac{{q}−{p}}{{c}}−\frac{\left({q}−{r}\right)}{{a}}\mathrm{cos}\:{B}\right]+\frac{\mathrm{16}{q}^{\mathrm{2}} {r}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\mathrm{sin}\:^{\mathrm{4}} {B}+\mathrm{4}{q}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:{B}\right)^{\mathrm{2}} \left(\frac{\mathrm{4}{qr}}{{a}^{\mathrm{2}} }\mathrm{sin}\:^{\mathrm{2}} {B}\right)}}{\mathrm{2}\left[\frac{{q}−{p}}{{c}}−\frac{\left({q}−{r}\right)}{{a}}\mathrm{cos}\:{B}\right]^{\mathrm{2}} −\frac{\mathrm{8}{qr}}{{a}^{\mathrm{2}} }\mathrm{sin}\:^{\mathrm{2}} {B}}\:\:\:\:\:\: \\ $$$$\:\:{with}\:\:\:\mathrm{cos}\:{B}\:=\:\frac{{c}^{\mathrm{2}} +{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{ac}} \\ $$$${and}\:\:\:\:{p}={s}−{a}\:,\:{q}={s}−{b}\:,\:{r}={s}−{c} \\ $$$$\blacksquare \\ $$
Commented by ajfour last updated on 15/Jul/19

$${if}\:\:{b}={c}={a}\:\:{then}\:\:{B}=\mathrm{60}°\:\:{and} \\ $$$${p}={q}={r}=\frac{{a}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\rho=\frac{\frac{\mathrm{3}{a}}{\mathrm{4}}−\sqrt{\frac{\mathrm{9}{a}^{\mathrm{2}} }{\mathrm{16}}+\frac{\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{16}}}}{−\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\Rightarrow\:\:\rho=\frac{{a}}{\:\sqrt{\mathrm{3}}}−\frac{{a}}{\mathrm{2}}\:\:\:\:\left({correct}\:{indeed}\right). \\ $$$$\:\:\:\:\:\:\:\rho_{{outer}} =\frac{{a}}{\:\sqrt{\mathrm{3}}}+\frac{{a}}{\mathrm{2}}\:. \\ $$
Commented by mr W last updated on 15/Jul/19
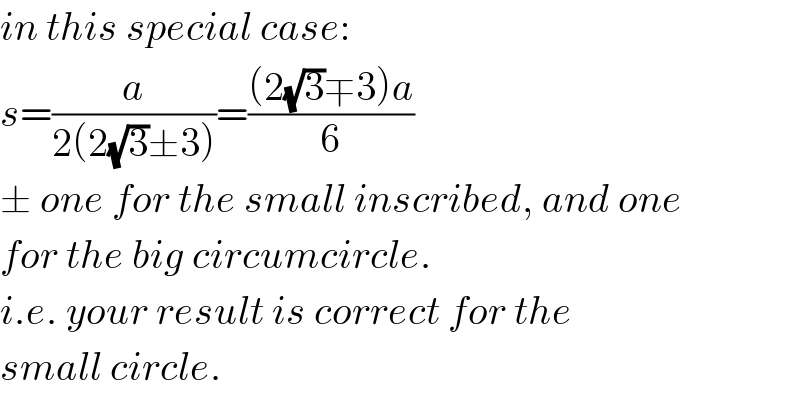
$${in}\:{this}\:{special}\:{case}: \\ $$$${s}=\frac{{a}}{\mathrm{2}\left(\mathrm{2}\sqrt{\mathrm{3}}\pm\mathrm{3}\right)}=\frac{\left(\mathrm{2}\sqrt{\mathrm{3}}\mp\mathrm{3}\right){a}}{\mathrm{6}} \\ $$$$\pm\:{one}\:{for}\:{the}\:{small}\:{inscribed},\:{and}\:{one} \\ $$$${for}\:{the}\:{big}\:{circumcircle}. \\ $$$${i}.{e}.\:{your}\:{result}\:{is}\:{correct}\:{for}\:{the} \\ $$$${small}\:{circle}. \\ $$
Commented by ajfour last updated on 15/Jul/19

Commented by ajfour last updated on 15/Jul/19

$${Thanks}\:{sir},\:{it}\:{turned}\:{right},\:{my} \\ $$$${faith}\:{in}\:{my}\:{second}\:{solution}; \\ $$$${for}\:{it}\:{was}\:{just}\:{a}\:{quadratic}. \\ $$$${can}\:{you}\:{try}\:{compressing}\:{my} \\ $$$${found}\:{result},\:{Sir}? \\ $$
Commented by mr W last updated on 16/Jul/19

$${the}\:{final}\:{result}\:{is} \\ $$$$\rho_{{i}} =\frac{\mathrm{1}}{\mathrm{2}\sqrt{\frac{\mathrm{1}}{{pq}}+\frac{\mathrm{1}}{{qr}}+\frac{\mathrm{1}}{{rp}}}+\left(\frac{\mathrm{1}}{{p}}+\frac{\mathrm{1}}{{q}}+\frac{\mathrm{1}}{{r}}\right)} \\ $$$$\rho_{{o}} =\frac{\mathrm{1}}{\mathrm{2}\sqrt{\frac{\mathrm{1}}{{pq}}+\frac{\mathrm{1}}{{qr}}+\frac{\mathrm{1}}{{rp}}}−\left(\frac{\mathrm{1}}{{p}}+\frac{\mathrm{1}}{{q}}+\frac{\mathrm{1}}{{r}}\right)} \\ $$
Answered by mr W last updated on 15/Jul/19
![a=q+r b=r+p c=p+q s=a+b+c ⇒p=s−a ⇒q=s−b ⇒r=s−c center of inscribed circle M MA=p+R MB=q+R MC=r+R cos θ_A =((MB^2 +MC^2 −a^2 )/(2MB×MC))=(((q+R)^2 +(r+R)^2 −a^2 )/(2(q+R)(r+R))) cos θ_B =(((r+R)^2 +(p+R)^2 −b^2 )/(2(r+R)(p+R))) cos θ_C =(((p+R)^2 +(q+R)^2 −c^2 )/(2(p+R)(q+R))) θ_A +θ_B +θ_C =2π cos (θ_A +θ_B )=cos (2π−θ_C ) (((q+R)^2 +(r+R)^2 −a^2 )/(2(q+R)(r+R)))×(((r+R)^2 +(p+R)^2 −b^2 )/(2(r+R)(p+R)))−((√({[2(q+R)(r+R)]^2 −[(q+R)^2 +(r+R)^2 −a^2 ]^2 }{[2(r+R)(p+R)]^2 −[(r+R)^2 +(p+R)^2 −b^2 ]^2 }))/(2(q+R)(r+R)2(r+R)(p+R)))=(((p+R)^2 +(q+R)^2 −c^2 )/(2(p+R)(q+R))) (({2R^2 +2(q+r)R+q^2 +r^2 −a^2 }{2R^2 +2(r+p)R+r^2 +p^2 −b^2 }−(√({[2(q+R)(r+R)]^2 −[(q+R)^2 +(r+R)^2 −a^2 ]^2 }{[2(r+R)(p+R)]^2 −[(r+R)^2 +(p+R)^2 −b^2 ]^2 })))/(2(r+R)^2 ))=2R^2 +2(p+q)R+p^2 +q^2 −c^2 {2R^2 +2(q+r)R+q^2 +r^2 −a^2 }{2R^2 +2(r+p)R+r^2 +p^2 −b^2 }−(√({(q+r+2R)^2 −a^2 }{a^2 −(q−r)^2 }{(r+p+2R)^2 −b^2 }{b^2 −(r−p)^2 }))=2(r+R)^2 {2R^2 +2(p+q)R+p^2 +q^2 −c^2 } {2R^2 +2(q+r)R+q^2 +r^2 −a^2 }{2R^2 +2(r+p)R+r^2 +p^2 −b^2 }−(√((q+r+2R+a)(q+r+2R−a)4qr(r+p+2R+b)(r+p+2R−b)4rp))=2(r+R)^2 {2R^2 +2(p+q)R+p^2 +q^2 −c^2 } {2R^2 +2(q+r)R−2qr}{2R^2 +2(r+p)R−2rp}−16Rr(√(pq(R+a)(R+b)))=2(r+R)^2 {2R^2 +2(p+q)R−2pq} {R^2 +(q+r)R−qr}{R^2 +(r+p)R−rp}−4Rr(√(pq(R+a)(R+b)))=(R^2 +2rR+r^2 ){R^2 +(p+q)R−pq} R^4 +(q+r)R^3 −qrR^2 +(r+p)R^3 +(q+r)(r+p)R^2 −qr(r+p)R−rpR^2 −rp(q+r)R+pqr^2 −4Rr(√(pq(R+a)(R+b)))=R^4 +2rR^3 +r^2 R^2 +(p+q)R^3 +2r(p+q)R^2 +r^2 (p+q)R−pqR^2 −2pqrR−pqr^2 (pq−qr−rp)R^2 −(p+q)r^2 R+pqr^2 =2Rr(√(pq(R+q+r)(R+r+p))) .....](https://www.tinkutara.com/question/Q64154.png)
$${a}={q}+{r} \\ $$$${b}={r}+{p} \\ $$$${c}={p}+{q} \\ $$$${s}={a}+{b}+{c} \\ $$$$\Rightarrow{p}={s}−{a} \\ $$$$\Rightarrow{q}={s}−{b} \\ $$$$\Rightarrow{r}={s}−{c} \\ $$$${center}\:{of}\:{inscribed}\:{circle}\:{M} \\ $$$${MA}={p}+{R} \\ $$$${MB}={q}+{R} \\ $$$${MC}={r}+{R} \\ $$$$\mathrm{cos}\:\theta_{{A}} =\frac{{MB}^{\mathrm{2}} +{MC}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{MB}×{MC}}=\frac{\left({q}+{R}\right)^{\mathrm{2}} +\left({r}+{R}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}\left({q}+{R}\right)\left({r}+{R}\right)} \\ $$$$\mathrm{cos}\:\theta_{{B}} =\frac{\left({r}+{R}\right)^{\mathrm{2}} +\left({p}+{R}\right)^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}\left({r}+{R}\right)\left({p}+{R}\right)} \\ $$$$\mathrm{cos}\:\theta_{{C}} =\frac{\left({p}+{R}\right)^{\mathrm{2}} +\left({q}+{R}\right)^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}\left({p}+{R}\right)\left({q}+{R}\right)} \\ $$$$\theta_{{A}} +\theta_{{B}} +\theta_{{C}} =\mathrm{2}\pi \\ $$$$\mathrm{cos}\:\left(\theta_{{A}} +\theta_{{B}} \right)=\mathrm{cos}\:\left(\mathrm{2}\pi−\theta_{{C}} \right) \\ $$$$\frac{\left({q}+{R}\right)^{\mathrm{2}} +\left({r}+{R}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}\left({q}+{R}\right)\left({r}+{R}\right)}×\frac{\left({r}+{R}\right)^{\mathrm{2}} +\left({p}+{R}\right)^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}\left({r}+{R}\right)\left({p}+{R}\right)}−\frac{\sqrt{\left\{\left[\mathrm{2}\left({q}+{R}\right)\left({r}+{R}\right)\right]^{\mathrm{2}} −\left[\left({q}+{R}\right)^{\mathrm{2}} +\left({r}+{R}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} \right]^{\mathrm{2}} \right\}\left\{\left[\mathrm{2}\left({r}+{R}\right)\left({p}+{R}\right)\right]^{\mathrm{2}} −\left[\left({r}+{R}\right)^{\mathrm{2}} +\left({p}+{R}\right)^{\mathrm{2}} −{b}^{\mathrm{2}} \right]^{\mathrm{2}} \right\}}}{\mathrm{2}\left({q}+{R}\right)\left({r}+{R}\right)\mathrm{2}\left({r}+{R}\right)\left({p}+{R}\right)}=\frac{\left({p}+{R}\right)^{\mathrm{2}} +\left({q}+{R}\right)^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}\left({p}+{R}\right)\left({q}+{R}\right)} \\ $$$$\frac{\left\{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{2}\left({q}+{r}\right){R}+{q}^{\mathrm{2}} +{r}^{\mathrm{2}} −{a}^{\mathrm{2}} \right\}\left\{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{2}\left({r}+{p}\right){R}+{r}^{\mathrm{2}} +{p}^{\mathrm{2}} −{b}^{\mathrm{2}} \right\}−\sqrt{\left\{\left[\mathrm{2}\left({q}+{R}\right)\left({r}+{R}\right)\right]^{\mathrm{2}} −\left[\left({q}+{R}\right)^{\mathrm{2}} +\left({r}+{R}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} \right]^{\mathrm{2}} \right\}\left\{\left[\mathrm{2}\left({r}+{R}\right)\left({p}+{R}\right)\right]^{\mathrm{2}} −\left[\left({r}+{R}\right)^{\mathrm{2}} +\left({p}+{R}\right)^{\mathrm{2}} −{b}^{\mathrm{2}} \right]^{\mathrm{2}} \right\}}}{\mathrm{2}\left({r}+{R}\right)^{\mathrm{2}} }=\mathrm{2}{R}^{\mathrm{2}} +\mathrm{2}\left({p}+{q}\right){R}+{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −{c}^{\mathrm{2}} \\ $$$$\left\{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{2}\left({q}+{r}\right){R}+{q}^{\mathrm{2}} +{r}^{\mathrm{2}} −{a}^{\mathrm{2}} \right\}\left\{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{2}\left({r}+{p}\right){R}+{r}^{\mathrm{2}} +{p}^{\mathrm{2}} −{b}^{\mathrm{2}} \right\}−\sqrt{\left\{\left({q}+{r}+\mathrm{2}{R}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} \right\}\left\{{a}^{\mathrm{2}} −\left({q}−{r}\right)^{\mathrm{2}} \right\}\left\{\left({r}+{p}+\mathrm{2}{R}\right)^{\mathrm{2}} −{b}^{\mathrm{2}} \right\}\left\{{b}^{\mathrm{2}} −\left({r}−{p}\right)^{\mathrm{2}} \right\}}=\mathrm{2}\left({r}+{R}\right)^{\mathrm{2}} \left\{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{2}\left({p}+{q}\right){R}+{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −{c}^{\mathrm{2}} \right\} \\ $$$$\left\{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{2}\left({q}+{r}\right){R}+{q}^{\mathrm{2}} +{r}^{\mathrm{2}} −{a}^{\mathrm{2}} \right\}\left\{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{2}\left({r}+{p}\right){R}+{r}^{\mathrm{2}} +{p}^{\mathrm{2}} −{b}^{\mathrm{2}} \right\}−\sqrt{\left({q}+{r}+\mathrm{2}{R}+{a}\right)\left({q}+{r}+\mathrm{2}{R}−{a}\right)\mathrm{4}{qr}\left({r}+{p}+\mathrm{2}{R}+{b}\right)\left({r}+{p}+\mathrm{2}{R}−{b}\right)\mathrm{4}{rp}}=\mathrm{2}\left({r}+{R}\right)^{\mathrm{2}} \left\{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{2}\left({p}+{q}\right){R}+{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −{c}^{\mathrm{2}} \right\} \\ $$$$\left\{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{2}\left({q}+{r}\right){R}−\mathrm{2}{qr}\right\}\left\{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{2}\left({r}+{p}\right){R}−\mathrm{2}{rp}\right\}−\mathrm{16}{Rr}\sqrt{{pq}\left({R}+{a}\right)\left({R}+{b}\right)}=\mathrm{2}\left({r}+{R}\right)^{\mathrm{2}} \left\{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{2}\left({p}+{q}\right){R}−\mathrm{2}{pq}\right\} \\ $$$$\left\{{R}^{\mathrm{2}} +\left({q}+{r}\right){R}−{qr}\right\}\left\{{R}^{\mathrm{2}} +\left({r}+{p}\right){R}−{rp}\right\}−\mathrm{4}{Rr}\sqrt{{pq}\left({R}+{a}\right)\left({R}+{b}\right)}=\left({R}^{\mathrm{2}} +\mathrm{2}{rR}+{r}^{\mathrm{2}} \right)\left\{{R}^{\mathrm{2}} +\left({p}+{q}\right){R}−{pq}\right\} \\ $$$${R}^{\mathrm{4}} +\left({q}+{r}\right){R}^{\mathrm{3}} −{qrR}^{\mathrm{2}} +\left({r}+{p}\right){R}^{\mathrm{3}} +\left({q}+{r}\right)\left({r}+{p}\right){R}^{\mathrm{2}} −{qr}\left({r}+{p}\right){R}−{rpR}^{\mathrm{2}} −{rp}\left({q}+{r}\right){R}+{pqr}^{\mathrm{2}} −\mathrm{4}{Rr}\sqrt{{pq}\left({R}+{a}\right)\left({R}+{b}\right)}={R}^{\mathrm{4}} +\mathrm{2}{rR}^{\mathrm{3}} +{r}^{\mathrm{2}} {R}^{\mathrm{2}} +\left({p}+{q}\right){R}^{\mathrm{3}} +\mathrm{2}{r}\left({p}+{q}\right){R}^{\mathrm{2}} +{r}^{\mathrm{2}} \left({p}+{q}\right){R}−{pqR}^{\mathrm{2}} −\mathrm{2}{pqrR}−{pqr}^{\mathrm{2}} \\ $$$$\left({pq}−{qr}−{rp}\right){R}^{\mathrm{2}} −\left({p}+{q}\right){r}^{\mathrm{2}} {R}+{pqr}^{\mathrm{2}} =\mathrm{2}{Rr}\sqrt{{pq}\left({R}+{q}+{r}\right)\left({R}+{r}+{p}\right)} \\ $$$$….. \\ $$
Commented by ajfour last updated on 15/Jul/19

$${This}\:{is}\:{injustice}\:{Sir}. \\ $$$${You}\:{should}\:{not}\:{effort}\:{limitless}.. \\ $$
Commented by mr W last updated on 14/Jul/19

$${this}\:{seems}\:{to}\:{be}\:{a}\:{tough}\:{way}\:{to}\:{obtain} \\ $$$${the}\:{radius}.\:{i}\:{think}\:{your}\:{first}\:{method} \\ $$$${with}\:{use}\:{of}\:\Delta\:{should}\:{be}\:{able}\:{to}\:{reach} \\ $$$${the}\:{goal}. \\ $$
