Question Number 64138 by Tawa1 last updated on 14/Jul/19
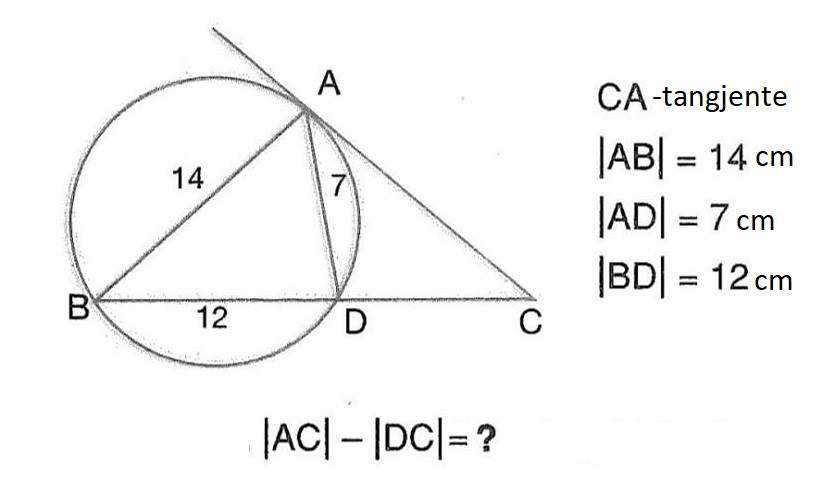
Answered by som(math1967) last updated on 14/Jul/19

$$\bigtriangleup{ADC}\sim\bigtriangleup{BAC} \\ $$$$\therefore\frac{{AC}}{{DC}}=\frac{{BC}}{{AC}}=\frac{{AB}}{{AD}} \\ $$$$\therefore\frac{{AC}}{{DC}}=\frac{{AB}}{{AD}}=\frac{\mathrm{14}}{\mathrm{7}}\:\:\therefore{AC}=\mathrm{2}{DC} \\ $$$${Again}\:\frac{{AC}}{{DC}}=\frac{{BC}}{{AC}}\:\Rightarrow{AC}^{\mathrm{2}} ={BC}×{DC} \\ $$$${AC}^{\mathrm{2}} =\left(\mathrm{12}+{DC}\right){DC}\bigstar \\ $$$$\Rightarrow{AC}^{\mathrm{2}} =\mathrm{12}{DC}+{DC}^{\mathrm{2}} \\ $$$$\Rightarrow{AC}^{\mathrm{2}} −{DC}^{\mathrm{2}} =\mathrm{12}{DC} \\ $$$$\Rightarrow\left({AC}+{DC}\right)\left({AC}−{DC}\right)=\mathrm{12}{DC} \\ $$$$\Rightarrow\mathrm{3}{DC}\left({AC}−{DC}\right)=\mathrm{12}{DC}\bigstar\bigstar \\ $$$${AC}−{DC}=\mathrm{4}{cm} \\ $$$$\bigstar{BC}={BD}+{DC}=\mathrm{12}+{DC} \\ $$$$\bigstar\bigstar{AC}+{DC}=\mathrm{2}{DC}+{DC}=\mathrm{3}{DC} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 16/Jul/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort}. \\ $$
