Question Number 64185 by Hope last updated on 15/Jul/19

Commented by Hope last updated on 15/Jul/19

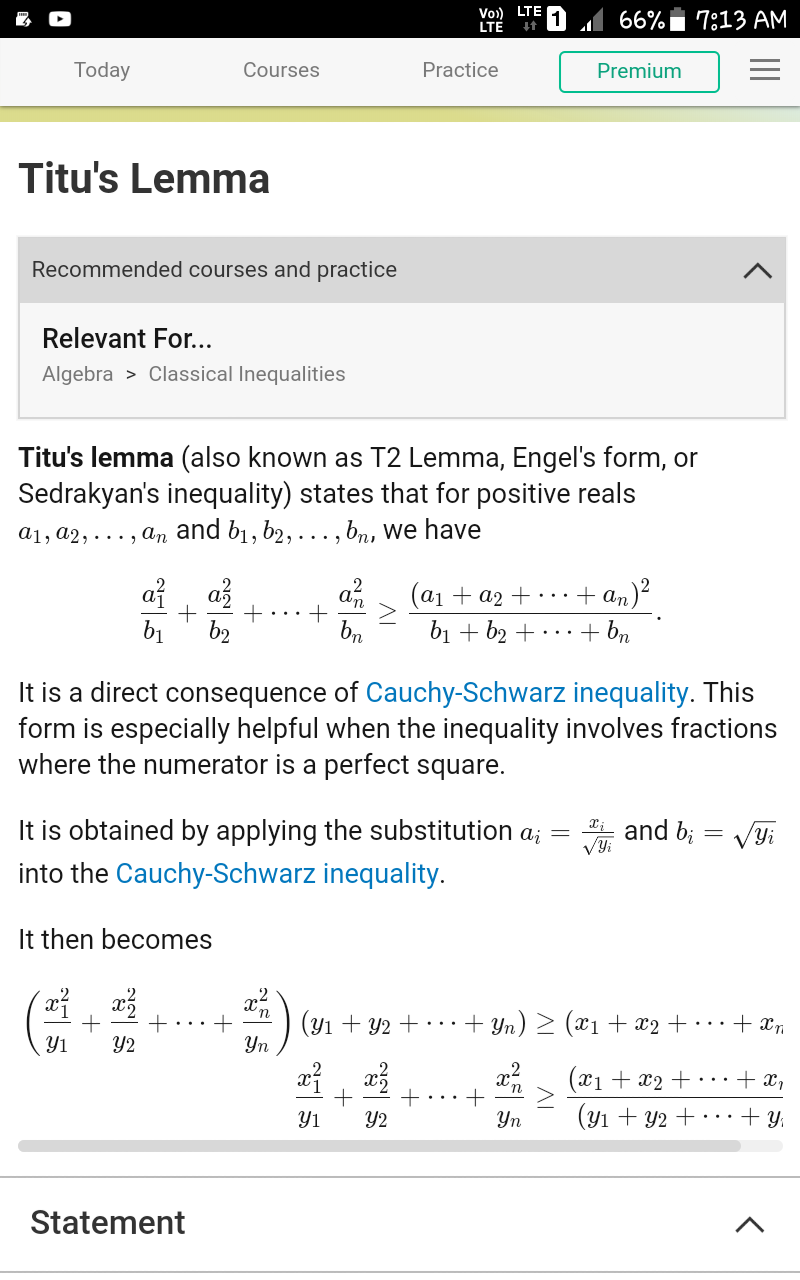
$${all}\:{question}\:{based}\:{on}\:{Tito}−{lemma}\:{inequality} \\ $$
Commented by Tony Lin last updated on 15/Jul/19
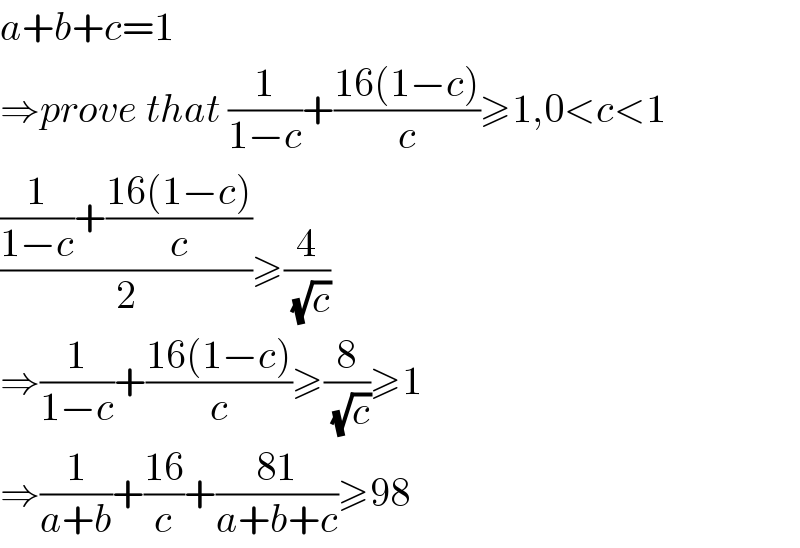
$${a}+{b}+{c}=\mathrm{1} \\ $$$$\Rightarrow{prove}\:{that}\:\frac{\mathrm{1}}{\mathrm{1}−{c}}+\frac{\mathrm{16}\left(\mathrm{1}−{c}\right)}{{c}}\geqslant\mathrm{1},\mathrm{0}<{c}<\mathrm{1} \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{1}−{c}}+\frac{\mathrm{16}\left(\mathrm{1}−{c}\right)}{{c}}}{\mathrm{2}}\geqslant\frac{\mathrm{4}}{\:\sqrt{{c}}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{1}−{c}}+\frac{\mathrm{16}\left(\mathrm{1}−{c}\right)}{{c}}\geqslant\frac{\mathrm{8}}{\:\sqrt{{c}}}\geqslant\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{a}+{b}}+\frac{\mathrm{16}}{{c}}+\frac{\mathrm{81}}{{a}+{b}+{c}}\geqslant\mathrm{98} \\ $$
Commented by Hope last updated on 15/Jul/19
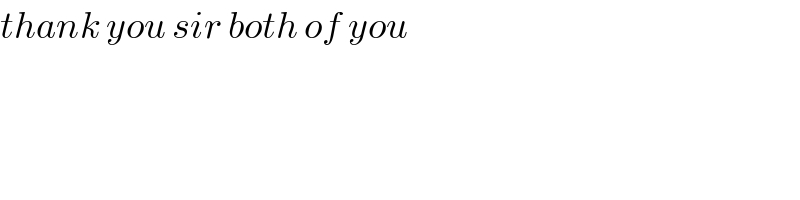
$${thank}\:{you}\:{sir}\:{both}\:{of}\:{you} \\ $$
Answered by MJS last updated on 15/Jul/19
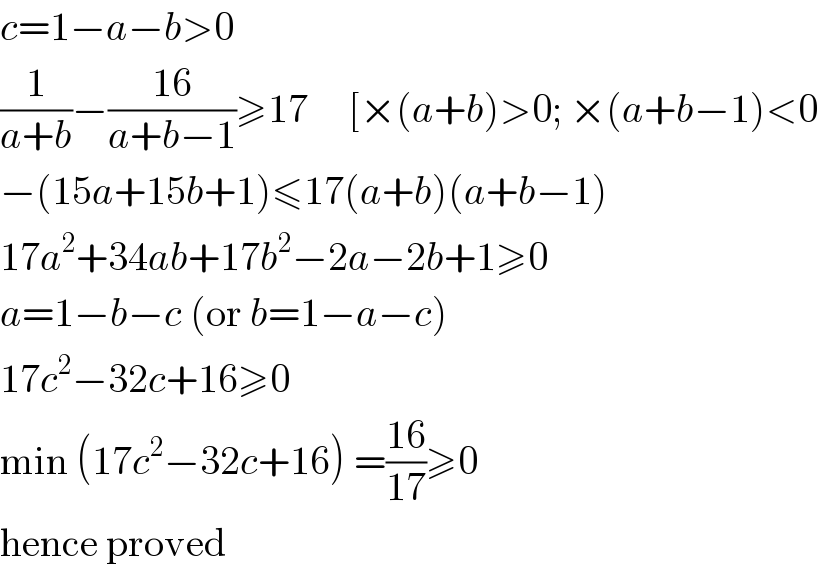
$${c}=\mathrm{1}−{a}−{b}>\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{a}+{b}}−\frac{\mathrm{16}}{{a}+{b}−\mathrm{1}}\geqslant\mathrm{17}\:\:\:\:\:\left[×\left({a}+{b}\right)>\mathrm{0};\:×\left({a}+{b}−\mathrm{1}\right)<\mathrm{0}\right. \\ $$$$−\left(\mathrm{15}{a}+\mathrm{15}{b}+\mathrm{1}\right)\leqslant\mathrm{17}\left({a}+{b}\right)\left({a}+{b}−\mathrm{1}\right) \\ $$$$\mathrm{17}{a}^{\mathrm{2}} +\mathrm{34}{ab}+\mathrm{17}{b}^{\mathrm{2}} −\mathrm{2}{a}−\mathrm{2}{b}+\mathrm{1}\geqslant\mathrm{0} \\ $$$${a}=\mathrm{1}−{b}−{c}\:\left(\mathrm{or}\:{b}=\mathrm{1}−{a}−{c}\right) \\ $$$$\mathrm{17}{c}^{\mathrm{2}} −\mathrm{32}{c}+\mathrm{16}\geqslant\mathrm{0} \\ $$$$\mathrm{min}\:\left(\mathrm{17}{c}^{\mathrm{2}} −\mathrm{32}{c}+\mathrm{16}\right)\:=\frac{\mathrm{16}}{\mathrm{17}}\geqslant\mathrm{0} \\ $$$$\mathrm{hence}\:\mathrm{proved} \\ $$
Commented by Hope last updated on 15/Jul/19

$${thank}\:{you}\:{sir}… \\ $$
Commented by Hope last updated on 15/Jul/19
Answered by Hope last updated on 15/Jul/19
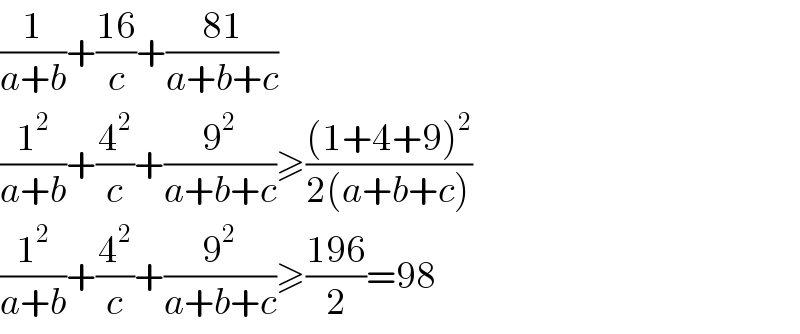
$$\frac{\mathrm{1}}{{a}+{b}}+\frac{\mathrm{16}}{{c}}+\frac{\mathrm{81}}{{a}+{b}+{c}} \\ $$$$\frac{\mathrm{1}^{\mathrm{2}} }{{a}+{b}}+\frac{\mathrm{4}^{\mathrm{2}} }{{c}}+\frac{\mathrm{9}^{\mathrm{2}} }{{a}+{b}+{c}}\geqslant\frac{\left(\mathrm{1}+\mathrm{4}+\mathrm{9}\right)^{\mathrm{2}} }{\mathrm{2}\left({a}+{b}+{c}\right)} \\ $$$$\frac{\mathrm{1}^{\mathrm{2}} }{{a}+{b}}+\frac{\mathrm{4}^{\mathrm{2}} }{{c}}+\frac{\mathrm{9}^{\mathrm{2}} }{{a}+{b}+{c}}\geqslant\frac{\mathrm{196}}{\mathrm{2}}=\mathrm{98}\: \\ $$
