Question Number 64187 by Hope last updated on 15/Jul/19

Answered by Hope last updated on 15/Jul/19
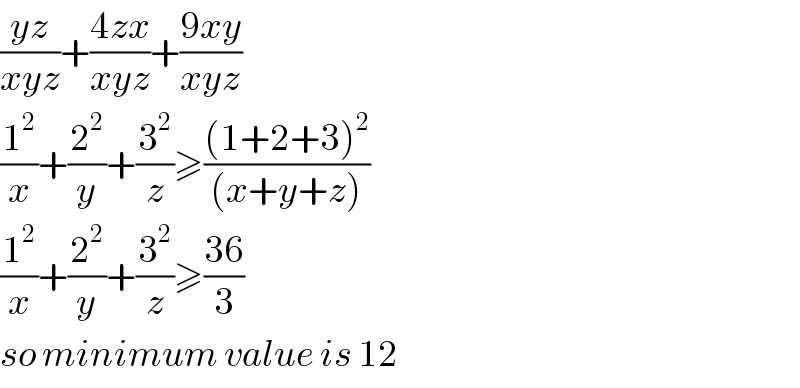
$$\frac{{yz}}{{xyz}}+\frac{\mathrm{4}{zx}}{{xyz}}+\frac{\mathrm{9}{xy}}{{xyz}} \\ $$$$\frac{\mathrm{1}^{\mathrm{2}} }{{x}}+\frac{\mathrm{2}^{\mathrm{2}} }{{y}}+\frac{\mathrm{3}^{\mathrm{2}} }{{z}}\geqslant\frac{\left(\mathrm{1}+\mathrm{2}+\mathrm{3}\right)^{\mathrm{2}} }{\left({x}+{y}+{z}\right)} \\ $$$$\frac{\mathrm{1}^{\mathrm{2}} }{{x}}+\frac{\mathrm{2}^{\mathrm{2}} }{{y}}+\frac{\mathrm{3}^{\mathrm{2}} }{{z}}\geqslant\frac{\mathrm{36}}{\mathrm{3}} \\ $$$${so}\:{minimum}\:{value}\:{is}\:\mathrm{12} \\ $$
