Question Number 64200 by aliesam last updated on 15/Jul/19

Commented by mathmax by abdo last updated on 15/Jul/19
![let I =∫_0 ^1 ((x−1)/(lnx))dx changement lnx=−t give x=e^(−t) I =−∫_0 ^∞ ((e^(−t) −1)/(−t))(−e^(−t) )dt =−∫_0 ^∞ ((e^(−2t) −e^(−t) )/t)dt let introduce the parametric function f(x) =∫_0 ^∞ ((e^(−2t) −e^(−t) )/t) e^(−xt) dt with x>0 we have f^′ (x) =−∫_0 ^∞ (e^(−2t) −e^(−t) )e^(−xt) dt =−∫_0 ^∞ { e^(−(x+2)t) −e^(−(x+1)t) }dt =∫_0 ^∞ (e^(−(x+1)t) −e^(−(x+2)t) )dt =[−(1/(x+1))e^(−(x+1)t) +(1/(x+2))e^(−(x+2)t) ]_0 ^(+∞) =(1/(x+1))−(1/(x+2)) ⇒f(x)=ln(x+1)−ln(x+2)+c=ln(((x+1)/(x+2))) +c ∃m>0 /∣f(x)∣≤m∫_0 ^∞ e^(−xt) dt =(m/x) →0 (x→+∞) c=lim_(x→+∞) (f(x)−ln(((x+1)/(x+2))))=0 f(x)=ln(((x+1)/(x+2))) I =lim_(x→0) −f(x) = ln(2) .](https://www.tinkutara.com/question/Q64212.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}−\mathrm{1}}{{lnx}}{dx}\:{changement}\:{lnx}=−{t}\:{give}\:{x}={e}^{−{t}} \\ $$$${I}\:=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{t}} −\mathrm{1}}{−{t}}\left(−{e}^{−{t}} \right){dt} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−\mathrm{2}{t}} −{e}^{−{t}} }{{t}}{dt}\:\:{let}\:{introduce}\:{the}\:{parametric}\:{function} \\ $$$${f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−\mathrm{2}{t}} −{e}^{−{t}} }{{t}}\:{e}^{−{xt}} {dt}\:\:{with}\:{x}>\mathrm{0}\:\:{we}\:{have}\: \\ $$$${f}^{'} \left({x}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\:\left({e}^{−\mathrm{2}{t}} −{e}^{−{t}} \right){e}^{−{xt}} \:{dt}\:=−\int_{\mathrm{0}} ^{\infty} \left\{\:\:{e}^{−\left({x}+\mathrm{2}\right){t}} −{e}^{−\left({x}+\mathrm{1}\right){t}} \right\}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left({e}^{−\left({x}+\mathrm{1}\right){t}} −{e}^{−\left({x}+\mathrm{2}\right){t}} \right){dt}\:=\left[−\frac{\mathrm{1}}{{x}+\mathrm{1}}{e}^{−\left({x}+\mathrm{1}\right){t}} +\frac{\mathrm{1}}{{x}+\mathrm{2}}\mathrm{e}^{−\left(\mathrm{x}+\mathrm{2}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{\mathrm{1}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{{x}+\mathrm{2}}\:\Rightarrow{f}\left({x}\right)={ln}\left({x}+\mathrm{1}\right)−{ln}\left({x}+\mathrm{2}\right)+{c}={ln}\left(\frac{{x}+\mathrm{1}}{{x}+\mathrm{2}}\right)\:+{c} \\ $$$$\exists{m}>\mathrm{0}\:/\mid{f}\left({x}\right)\mid\leqslant{m}\int_{\mathrm{0}} ^{\infty} \:{e}^{−{xt}} {dt}\:=\frac{{m}}{{x}}\:\rightarrow\mathrm{0}\:\left({x}\rightarrow+\infty\right)\: \\ $$$${c}={lim}_{{x}\rightarrow+\infty} \left({f}\left({x}\right)−{ln}\left(\frac{{x}+\mathrm{1}}{{x}+\mathrm{2}}\right)\right)=\mathrm{0}\:\:{f}\left({x}\right)={ln}\left(\frac{{x}+\mathrm{1}}{{x}+\mathrm{2}}\right) \\ $$$${I}\:={lim}_{{x}\rightarrow\mathrm{0}} \:\:−{f}\left({x}\right)\:=\:{ln}\left(\mathrm{2}\right)\:. \\ $$
Answered by Hope last updated on 15/Jul/19
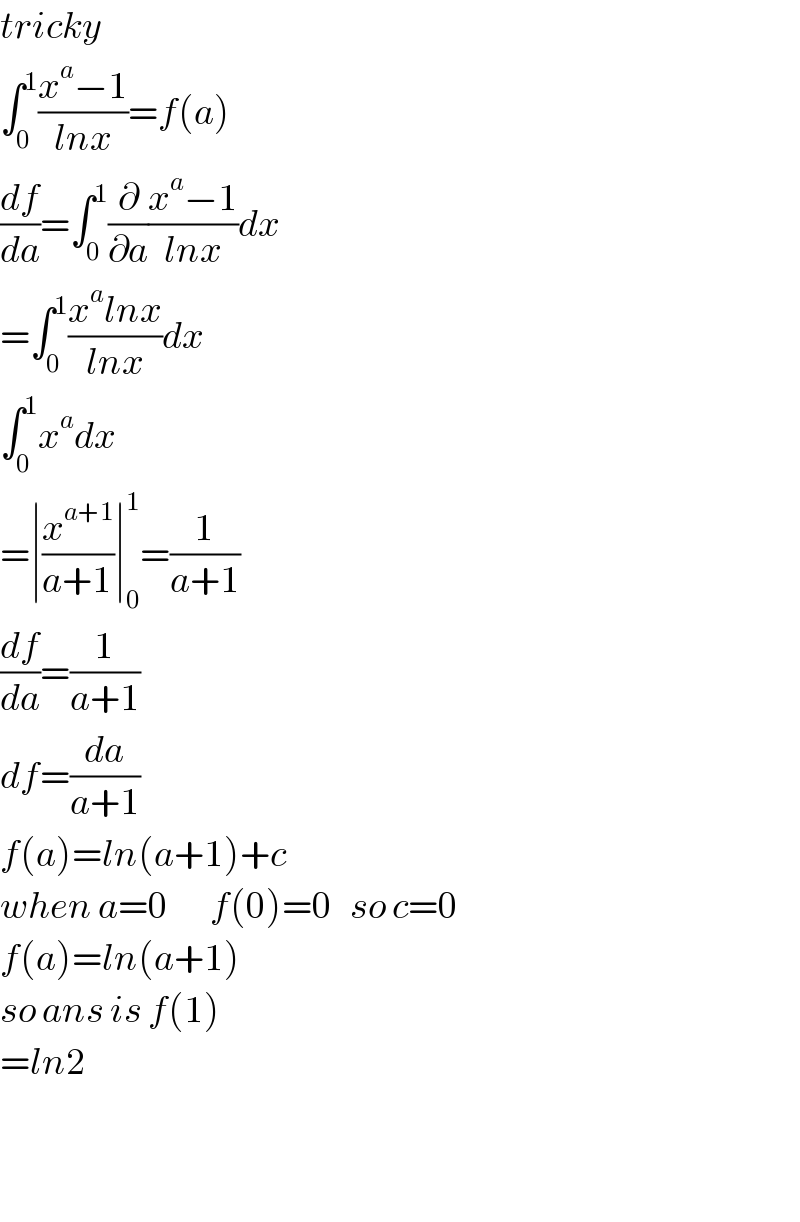
$${tricky} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} −\mathrm{1}}{{lnx}}={f}\left({a}\right) \\ $$$$\frac{{df}}{{da}}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\partial}{\partial{a}}\frac{{x}^{{a}} −\mathrm{1}}{{lnx}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} {lnx}}{{lnx}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{a}} {dx} \\ $$$$=\mid\frac{{x}^{{a}+\mathrm{1}} }{{a}+\mathrm{1}}\mid_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{{a}+\mathrm{1}} \\ $$$$\frac{{df}}{{da}}=\frac{\mathrm{1}}{{a}+\mathrm{1}} \\ $$$${df}=\frac{{da}}{{a}+\mathrm{1}} \\ $$$${f}\left({a}\right)={ln}\left({a}+\mathrm{1}\right)+{c} \\ $$$${when}\:{a}=\mathrm{0}\:\:\:\:\:\:\:{f}\left(\mathrm{0}\right)=\mathrm{0}\:\:\:{so}\:{c}=\mathrm{0} \\ $$$${f}\left({a}\right)={ln}\left({a}+\mathrm{1}\right) \\ $$$${so}\:{ans}\:{is}\:{f}\left(\mathrm{1}\right) \\ $$$$={ln}\mathrm{2} \\ $$$$ \\ $$$$ \\ $$
