Question Number 64287 by aliesam last updated on 16/Jul/19

Commented by mathmax by abdo last updated on 16/Jul/19
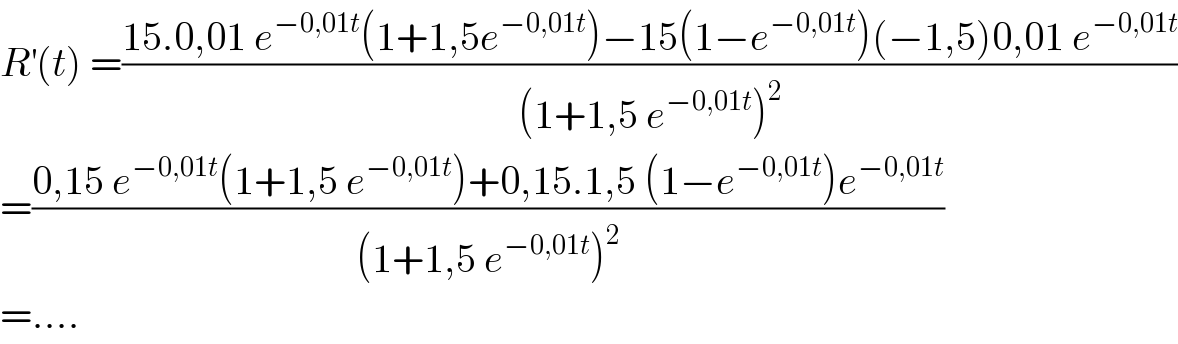
$${R}^{'} \left({t}\right)\:=\frac{\mathrm{15}.\mathrm{0},\mathrm{01}\:{e}^{−\mathrm{0},\mathrm{01}{t}} \left(\mathrm{1}+\mathrm{1},\mathrm{5}{e}^{−\mathrm{0},\mathrm{01}{t}} \right)−\mathrm{15}\left(\mathrm{1}−{e}^{−\mathrm{0},\mathrm{01}{t}} \right)\left(−\mathrm{1},\mathrm{5}\right)\mathrm{0},\mathrm{01}\:{e}^{−\mathrm{0},\mathrm{01}{t}} }{\left(\mathrm{1}+\mathrm{1},\mathrm{5}\:{e}^{−\mathrm{0},\mathrm{01}{t}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{0},\mathrm{15}\:{e}^{−\mathrm{0},\mathrm{01}{t}} \left(\mathrm{1}+\mathrm{1},\mathrm{5}\:{e}^{−\mathrm{0},\mathrm{01}{t}} \right)+\mathrm{0},\mathrm{15}.\mathrm{1},\mathrm{5}\:\left(\mathrm{1}−{e}^{−\mathrm{0},\mathrm{01}{t}} \right){e}^{−\mathrm{0},\mathrm{01}{t}} }{\left(\mathrm{1}+\mathrm{1},\mathrm{5}\:{e}^{−\mathrm{0},\mathrm{01}{t}} \right)^{\mathrm{2}} } \\ $$$$=…. \\ $$
Commented by aliesam last updated on 16/Jul/19

$${thank}\:{you}\:{sir}\: \\ $$
Commented by mathmax by abdo last updated on 17/Jul/19
$${you}\:{are}\:{welcome}. \\ $$
