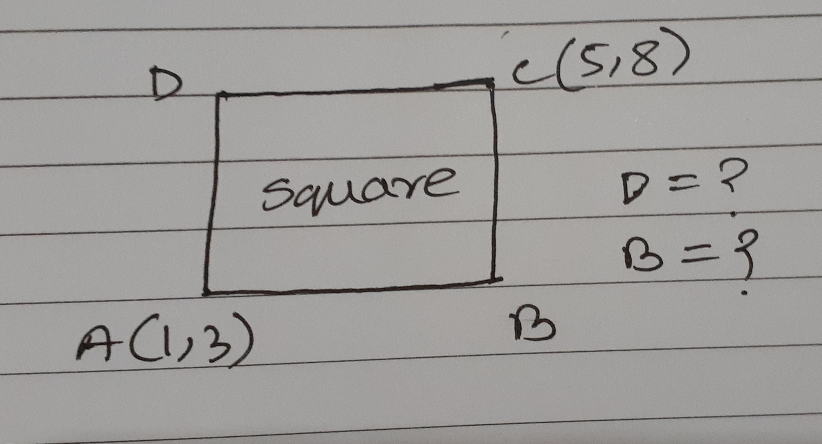
Question Number 64309 by aseer imad last updated on 16/Jul/19
Commented by Tony Lin last updated on 17/Jul/19
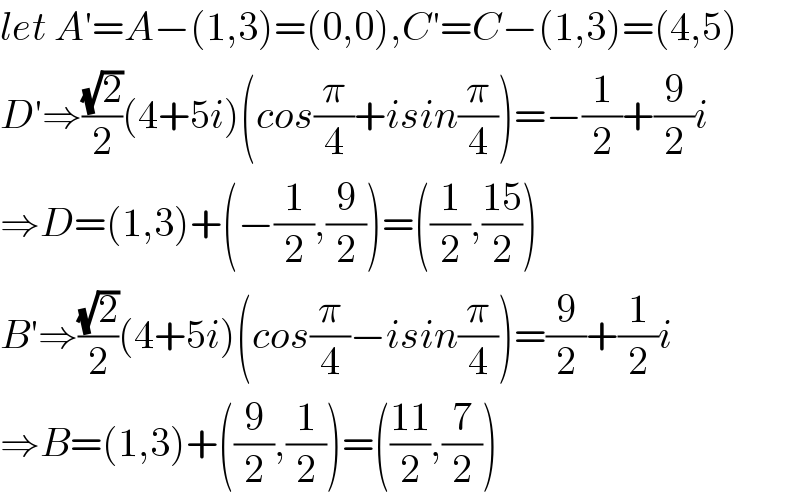
$${let}\:{A}'={A}−\left(\mathrm{1},\mathrm{3}\right)=\left(\mathrm{0},\mathrm{0}\right),{C}'={C}−\left(\mathrm{1},\mathrm{3}\right)=\left(\mathrm{4},\mathrm{5}\right) \\ $$$${D}'\Rightarrow\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{4}+\mathrm{5}{i}\right)\left({cos}\frac{\pi}{\mathrm{4}}+{isin}\frac{\pi}{\mathrm{4}}\right)=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{9}}{\mathrm{2}}{i} \\ $$$$\Rightarrow{D}=\left(\mathrm{1},\mathrm{3}\right)+\left(−\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{9}}{\mathrm{2}}\right)=\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{15}}{\mathrm{2}}\right) \\ $$$${B}'\Rightarrow\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{4}+\mathrm{5}{i}\right)\left({cos}\frac{\pi}{\mathrm{4}}−{isin}\frac{\pi}{\mathrm{4}}\right)=\frac{\mathrm{9}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{i} \\ $$$$\Rightarrow{B}=\left(\mathrm{1},\mathrm{3}\right)+\left(\frac{\mathrm{9}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)=\left(\frac{\mathrm{11}}{\mathrm{2}},\frac{\mathrm{7}}{\mathrm{2}}\right) \\ $$
