Menu Close

Question-64311

Tinku Tara 0 Comments
Pin




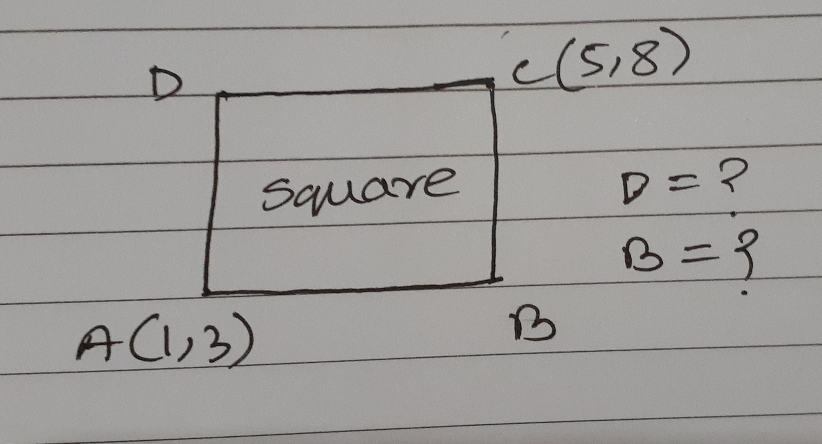
Question Number 64311 by aseer imad last updated on 16/Jul/19
Commented by Tony Lin last updated on 17/Jul/19
letA′=A−(1,3)=(0,0),C′=C−(1,3)=(4,5) D′= [((((√2)/2) 0)),((0 ((√2)/2))) ] [((cos(π/4) −sin(π/4))),((sin(π/4) cos(π/4))) ] [(4),(5) ] = [(((1/2) −(1/2))),(((1/2) (1/2))) ] [(4),(5) ] = [((−(1/2))),(( (9/2))) ] ⇒D=D′+(1,3)=((1/2),((15)/2)) ∵AB^⇀ =DC^⇀ ∴B=(1,3)+((9/2),(1/2))=(((11)/2),(7/2))
$${letA}'={A}−\left(\mathrm{1},\mathrm{3}\right)=\left(\mathrm{0},\mathrm{0}\right),{C}'={C}−\left(\mathrm{1},\mathrm{3}\right)=\left(\mathrm{4},\mathrm{5}\right) \\ $$$${D}'=\begin{bmatrix}{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\end{bmatrix}\begin{bmatrix}{{cos}\frac{\pi}{\mathrm{4}}\:\:−{sin}\frac{\pi}{\mathrm{4}}}\\{{sin}\frac{\pi}{\mathrm{4}}\:\:\:\:\:\:{cos}\frac{\pi}{\mathrm{4}}}\end{bmatrix}\begin{bmatrix}{\mathrm{4}}\\{\mathrm{5}}\end{bmatrix} \\ $$$$\:\:\:\:\:\:\:=\begin{bmatrix}{\frac{\mathrm{1}}{\mathrm{2}}\:\:−\frac{\mathrm{1}}{\mathrm{2}}}\\{\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}}\end{bmatrix}\begin{bmatrix}{\mathrm{4}}\\{\mathrm{5}}\end{bmatrix} \\ $$$$\:\:\:\:\:\:\:\:=\begin{bmatrix}{−\frac{\mathrm{1}}{\mathrm{2}}}\\{\:\:\:\:\frac{\mathrm{9}}{\mathrm{2}}}\end{bmatrix} \\ $$$$\Rightarrow{D}={D}'+\left(\mathrm{1},\mathrm{3}\right)=\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{15}}{\mathrm{2}}\right) \\ $$$$\because{A}\overset{\rightharpoonup} {{B}}={D}\overset{\rightharpoonup} {{C}} \\ $$$$\therefore{B}=\left(\mathrm{1},\mathrm{3}\right)+\left(\frac{\mathrm{9}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)=\left(\frac{\mathrm{11}}{\mathrm{2}},\frac{\mathrm{7}}{\mathrm{2}}\right) \\ $$
Answered by Tanmay chaudhury last updated on 16/Jul/19
AC (y−3)=((8−3)/(5−1))(x−1) y−3=(5/4)(x−1) 4y−5x−12+5=0 4y−5x−7=0 is ean AC let eqn AB (y−3)=m(x−1) angle betwee AB and AC is (π/4) tan(π/4)=((m−(5/4))/(1+m×(5/4))) 1+((5m)/4)=m−(5/4) ((5m)/4)−m=((−5)/4)−1 (m/4)=((−9)/4) m=−9 AB (y−3)=((−9)/1)(x−1) y−3+9x−9=0 y+9x−12=0 ←eqn AB DC (y−8)=((−9)/1)(x−5) y−8+9x−45=0 y+9x−53=0 ←eqn DC again tan(π/4)=(((5/4)−m)/(1+((5m)/4))) 1+((5m)/4)=(5/4)−m ((9m)/4)=(1/4) m=(1/9) eqn AD (y−3)=(1/9)(x−1) 9y−27−x+1=0 9y−x−26=0 ←eqn AD BC (y−8)=(1/9)(x−5) 9y−72=x−5 9y−x−67=0 ←eqn BC solve eqn DC y+9x−53=0 and AD 9y−x−26=0 to find D y+9(9y−26)−53=0 82y−234−53=0 y=((287)/(82))=(7/2) so x=9×(7/2)−26 D(((63−52)/2),(7/2)) so D(((11)/2),(7/2)) solveAB y+9x−12=0 BC 9y−x−67=0 y+9(9y−67)−12=0 82y=603+12 y=((615)/(82))=((15)/2) x=9×((15)/2)−67 x=((135−134)/2)=(1/2) B((1/2),((15)/2)) so A(1,3) B((1/2),((15)/2)),C(5,8) D(((11)/2),(7/2)) pls check Tanmay 16.07.19
$${AC}\:\:\left({y}−\mathrm{3}\right)=\frac{\mathrm{8}−\mathrm{3}}{\mathrm{5}−\mathrm{1}}\left({x}−\mathrm{1}\right) \\ $$$${y}−\mathrm{3}=\frac{\mathrm{5}}{\mathrm{4}}\left({x}−\mathrm{1}\right) \\ $$$$\mathrm{4}{y}−\mathrm{5}{x}−\mathrm{12}+\mathrm{5}=\mathrm{0}\:\:\:\:\mathrm{4}{y}−\mathrm{5}{x}−\mathrm{7}=\mathrm{0}\:\:{is}\:{ean}\:{AC} \\ $$$${let}\:{eqn}\:{AB}\:\left({y}−\mathrm{3}\right)={m}\left({x}−\mathrm{1}\right) \\ $$$${angle}\:{betwee}\:{AB}\:{and}\:{AC}\:{is}\:\frac{\pi}{\mathrm{4}} \\ $$$${tan}\frac{\pi}{\mathrm{4}}=\frac{{m}−\frac{\mathrm{5}}{\mathrm{4}}}{\mathrm{1}+{m}×\frac{\mathrm{5}}{\mathrm{4}}} \\ $$$$\mathrm{1}+\frac{\mathrm{5}{m}}{\mathrm{4}}={m}−\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\frac{\mathrm{5}{m}}{\mathrm{4}}−{m}=\frac{−\mathrm{5}}{\mathrm{4}}−\mathrm{1} \\ $$$$\frac{{m}}{\mathrm{4}}=\frac{−\mathrm{9}}{\mathrm{4}}\:\:\:{m}=−\mathrm{9} \\ $$$${AB}\:\:\left({y}−\mathrm{3}\right)=\frac{−\mathrm{9}}{\mathrm{1}}\left({x}−\mathrm{1}\right) \\ $$$${y}−\mathrm{3}+\mathrm{9}{x}−\mathrm{9}=\mathrm{0} \\ $$$${y}+\mathrm{9}{x}−\mathrm{12}=\mathrm{0}\:\leftarrow{eqn}\:{AB} \\ $$$${DC}\:\:\left({y}−\mathrm{8}\right)=\frac{−\mathrm{9}}{\mathrm{1}}\left({x}−\mathrm{5}\right) \\ $$$${y}−\mathrm{8}+\mathrm{9}{x}−\mathrm{45}=\mathrm{0} \\ $$$${y}+\mathrm{9}{x}−\mathrm{53}=\mathrm{0}\:\:\leftarrow{eqn}\:{DC} \\ $$$${again}\:{tan}\frac{\pi}{\mathrm{4}}=\frac{\frac{\mathrm{5}}{\mathrm{4}}−{m}}{\mathrm{1}+\frac{\mathrm{5}{m}}{\mathrm{4}}} \\ $$$$\mathrm{1}+\frac{\mathrm{5}{m}}{\mathrm{4}}=\frac{\mathrm{5}}{\mathrm{4}}−{m} \\ $$$$\frac{\mathrm{9}{m}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}}\:\:{m}=\frac{\mathrm{1}}{\mathrm{9}} \\ $$$${eqn}\:\:{AD}\:\:\left({y}−\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{9}}\left({x}−\mathrm{1}\right) \\ $$$$\mathrm{9}{y}−\mathrm{27}−{x}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{9}{y}−{x}−\mathrm{26}=\mathrm{0}\:\:\leftarrow{eqn}\:{AD}\: \\ $$$${BC}\:\left({y}−\mathrm{8}\right)=\frac{\mathrm{1}}{\mathrm{9}}\left({x}−\mathrm{5}\right) \\ $$$$\mathrm{9}{y}−\mathrm{72}={x}−\mathrm{5} \\ $$$$\mathrm{9}{y}−{x}−\mathrm{67}=\mathrm{0}\:\leftarrow{eqn}\:{BC} \\ $$$${solve}\:{eqn}\:{DC}\:\:{y}+\mathrm{9}{x}−\mathrm{53}=\mathrm{0}\:{and}\:{AD}\:\mathrm{9}{y}−{x}−\mathrm{26}=\mathrm{0} \\ $$$${to}\:{find}\:{D}\:\:{y}+\mathrm{9}\left(\mathrm{9}{y}−\mathrm{26}\right)−\mathrm{53}=\mathrm{0} \\ $$$$\mathrm{82}{y}−\mathrm{234}−\mathrm{53}=\mathrm{0} \\ $$$${y}=\frac{\mathrm{287}}{\mathrm{82}}=\frac{\mathrm{7}}{\mathrm{2}}\:\:\:{so}\:{x}=\mathrm{9}×\frac{\mathrm{7}}{\mathrm{2}}−\mathrm{26} \\ $$$${D}\left(\frac{\mathrm{63}−\mathrm{52}}{\mathrm{2}},\frac{\mathrm{7}}{\mathrm{2}}\right)\:\:{so}\:\boldsymbol{{D}}\left(\frac{\mathrm{11}}{\mathrm{2}},\frac{\mathrm{7}}{\mathrm{2}}\right) \\ $$$${solveAB}\:{y}+\mathrm{9}{x}−\mathrm{12}=\mathrm{0}\:{BC}\:\mathrm{9}{y}−{x}−\mathrm{67}=\mathrm{0} \\ $$$${y}+\mathrm{9}\left(\mathrm{9}{y}−\mathrm{67}\right)−\mathrm{12}=\mathrm{0} \\ $$$$\mathrm{82}{y}=\mathrm{603}+\mathrm{12}\:\:\:\:\:{y}=\frac{\mathrm{615}}{\mathrm{82}}=\frac{\mathrm{15}}{\mathrm{2}} \\ $$$${x}=\mathrm{9}×\frac{\mathrm{15}}{\mathrm{2}}−\mathrm{67} \\ $$$${x}=\frac{\mathrm{135}−\mathrm{134}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${B}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{15}}{\mathrm{2}}\right)\:{so} \\ $$$${A}\left(\mathrm{1},\mathrm{3}\right)\:{B}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{15}}{\mathrm{2}}\right),{C}\left(\mathrm{5},\mathrm{8}\right)\:\:{D}\left(\frac{\mathrm{11}}{\mathrm{2}},\frac{\mathrm{7}}{\mathrm{2}}\right)\:\:{pls}\:{check}\: \\ $$$${Tanmay}\:\mathrm{16}.\mathrm{07}.\mathrm{19} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by aseer imad last updated on 16/Jul/19
Thank you very much sir,it is right. Could've avoid the complexity of finding all equations. Instead finding one vertex and use mid point to find the other...
Commented by Tanmay chaudhury last updated on 17/Jul/19
i am going to rechek the steps..
$${i}\:{am}\:{going}\:{to}\:{rechek}\:{the}\:{steps}.. \\ $$
Answered by mr W last updated on 16/Jul/19
M=midpoint of AC=midpoint of BD M(((1+5)/2),((3+8)/2))=M(3,((11)/2)) Δx_(MB) =Δy_(AM) =((11)/2)−3=(5/2) ⇒x_B =3+(5/2)=((11)/2) Δy_(MB) =Δx_(AM) =3−1=2 ⇒y_B =((11)/2)−2=(7/2) ((x_D +((11)/2))/2)=3 ⇒x_D =6−((11)/2)=(1/2) ((y_D +(7/2))/2)=((11)/2) ⇒y_D =11−(7/2)=((15)/2) ⇒B(((11)/2),(7/2)), D((1/2),((15)/2))
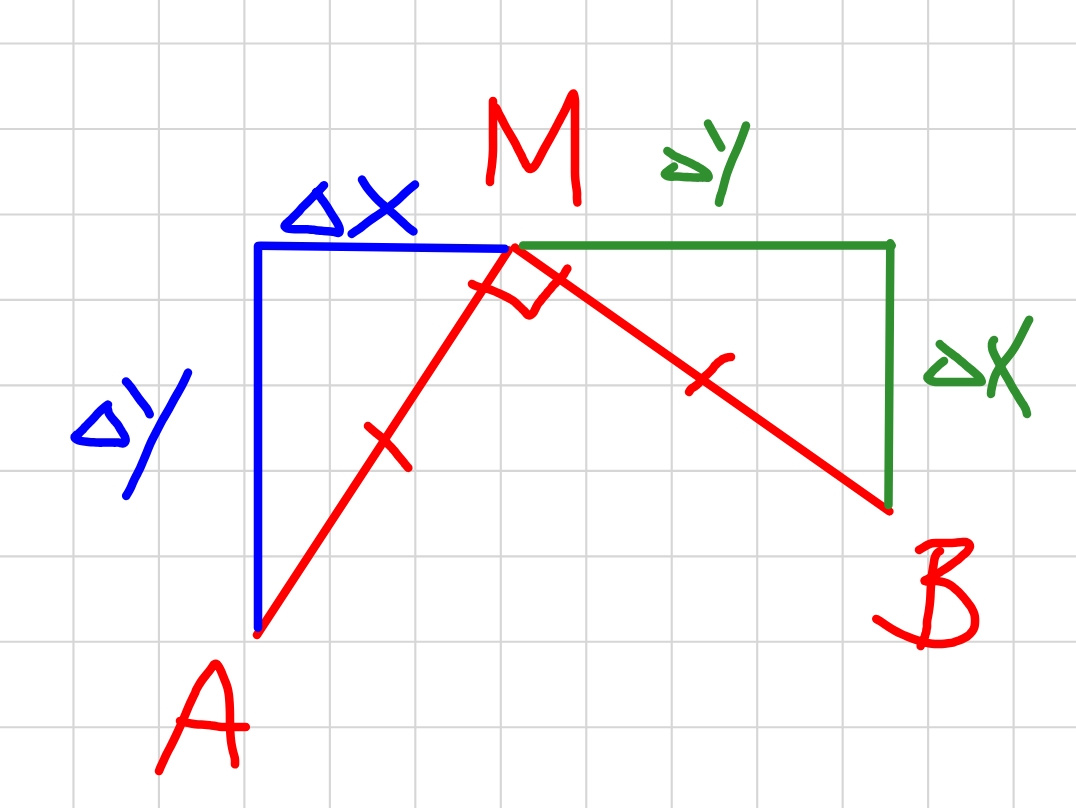
$${M}={midpoint}\:{of}\:{AC}={midpoint}\:{of}\:{BD} \\ $$$${M}\left(\frac{\mathrm{1}+\mathrm{5}}{\mathrm{2}},\frac{\mathrm{3}+\mathrm{8}}{\mathrm{2}}\right)={M}\left(\mathrm{3},\frac{\mathrm{11}}{\mathrm{2}}\right) \\ $$$$\Delta{x}_{{MB}} =\Delta{y}_{{AM}} =\frac{\mathrm{11}}{\mathrm{2}}−\mathrm{3}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\Rightarrow{x}_{{B}} =\mathrm{3}+\frac{\mathrm{5}}{\mathrm{2}}=\frac{\mathrm{11}}{\mathrm{2}} \\ $$$$\Delta{y}_{{MB}} =\Delta{x}_{{AM}} =\mathrm{3}−\mathrm{1}=\mathrm{2} \\ $$$$\Rightarrow{y}_{{B}} =\frac{\mathrm{11}}{\mathrm{2}}−\mathrm{2}=\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$\frac{{x}_{{D}} +\frac{\mathrm{11}}{\mathrm{2}}}{\mathrm{2}}=\mathrm{3} \\ $$$$\Rightarrow{x}_{{D}} =\mathrm{6}−\frac{\mathrm{11}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{y}_{{D}} +\frac{\mathrm{7}}{\mathrm{2}}}{\mathrm{2}}=\frac{\mathrm{11}}{\mathrm{2}} \\ $$$$\Rightarrow{y}_{{D}} =\mathrm{11}−\frac{\mathrm{7}}{\mathrm{2}}=\frac{\mathrm{15}}{\mathrm{2}} \\ $$$$\Rightarrow{B}\left(\frac{\mathrm{11}}{\mathrm{2}},\frac{\mathrm{7}}{\mathrm{2}}\right),\:{D}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{15}}{\mathrm{2}}\right) \\ $$
Commented by mr W last updated on 17/Jul/19
Answered by ajfour last updated on 17/Jul/19
Commented by ajfour last updated on 17/Jul/19
B(1+4+(1/2) , 3+(1/2)) ⇒ B(((11)/2),(7/2)) D(1−(1/2), 3+(1/2)+4) ⇒ D((1/2),((15)/2)) .
$${B}\left(\mathrm{1}+\mathrm{4}+\frac{\mathrm{1}}{\mathrm{2}}\:,\:\mathrm{3}+\frac{\mathrm{1}}{\mathrm{2}}\right)\:\Rightarrow\:{B}\left(\frac{\mathrm{11}}{\mathrm{2}},\frac{\mathrm{7}}{\mathrm{2}}\right) \\ $$$${D}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}},\:\mathrm{3}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{4}\right)\:\Rightarrow\:{D}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{15}}{\mathrm{2}}\right)\:. \\ $$
Commented by aseer imad last updated on 22/Jul/19
Cool! thanks

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *