Question Number 64404 by aliesam last updated on 17/Jul/19
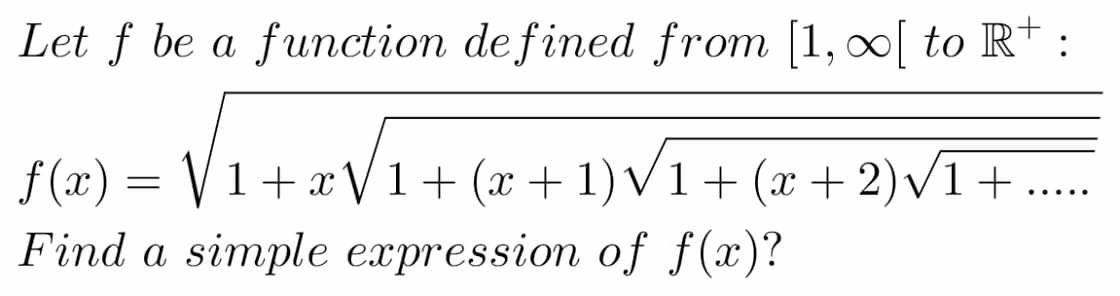
Commented by Prithwish sen last updated on 17/Jul/19

$$\mathrm{x}+\mathrm{1}\:=\:\sqrt{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:}\:=\:\sqrt{\mathrm{1}+\mathrm{x}\left(\mathrm{x}+\mathrm{2}\right)}\:=\:\sqrt{\mathrm{1}+\mathrm{x}\sqrt{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} }} \\ $$$$=\:\sqrt{\mathrm{1}+\mathrm{x}\sqrt{\mathrm{1}+\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{3}\right)}\:}\:=\:\sqrt{\mathrm{1}+\mathrm{x}\sqrt{\mathrm{1}+\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{2}} }}} \\ $$$$=\:\sqrt{\mathrm{1}+\mathrm{x}\sqrt{\mathrm{1}+\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{1}+\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}+\mathrm{4}\right)}}\:} \\ $$$$=\sqrt{\mathrm{1}+\mathrm{x}\sqrt{\mathrm{1}+\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{1}+\left(\mathrm{x}+\mathrm{2}\right)\sqrt{\mathrm{1}+….}}}} \\ $$$$\therefore\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{x}+\mathrm{1}\:\mathrm{please}\:\mathrm{check}. \\ $$
Commented by aliesam last updated on 17/Jul/19

$${thank}\:{you}\:{sir}\:{that}\:{is}\:{the}\:{right}\:{result}. \\ $$$${but}\:{i}\:{have}\:{one}\:{thing}\:{to}\:{say},{about}\:{the}\:{passage}\:{to}\:{the}\:{conclusion}. \\ $$$${you}\:{assumed}\:{that}\:{is}\:{correct} \\ $$$${based}\:{on}\:{observation},{how}\:{can}\:{we}\:{prove}\:{that}\:{f}\left({x}\right) \\ $$$${is}\:{written}\:{like}\:{that}\:{in}\:{general}\:{case}. \\ $$$${you}\:{cannot}\:{use}\:{induction}\:{principle}\:{to}\:{prove}\:{it} \\ $$$${because}\:{the}\:{variable}\:{is}\:{not}\:{an}\:{integer},{its} \\ $$$$\:{real}\:{positive}\:{number}.{but}\:{its}\:{good}\:{jop}\:{god}\:{bless}\:{you} \\ $$
Commented by Prithwish sen last updated on 17/Jul/19

$$\mathrm{Yes}\:\mathrm{sir}\:\mathrm{you}\:\mathrm{are}\:\mathrm{right}.\:\mathrm{There}\:\mathrm{is}\:\mathrm{no}\:\mathrm{such}\:\mathrm{process} \\ $$$$\mathrm{atleast}\:\mathrm{not}\:\mathrm{known}\:\mathrm{to}\:\mathrm{me}\:\mathrm{right}\:\mathrm{now}. \\ $$
Commented by mr W last updated on 17/Jul/19

$${generally} \\ $$$${x}+{n}= \\ $$$$=\sqrt{\left({x}+{n}\right)^{\mathrm{2}} } \\ $$$$=\sqrt{\mathrm{1}+\left({x}+{n}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\sqrt{\mathrm{1}+\left({x}+{n}−\mathrm{1}\right)\left({x}+{n}+\mathrm{1}\right)} \\ $$$$=\sqrt{\mathrm{1}+\left({x}+{n}−\mathrm{1}\right)\sqrt{\mathrm{1}+\left({x}+{n}\right)\left({x}+{n}+\mathrm{2}\right)}} \\ $$$$=\sqrt{\mathrm{1}+\left({x}+{n}−\mathrm{1}\right)\sqrt{\mathrm{1}+\left({x}+{n}\right)\sqrt{\mathrm{1}+\left({x}+{n}+\mathrm{1}\right)\left({x}+{n}+\mathrm{3}\right)}}} \\ $$$$…. \\ $$$${with}\:{x}=\mathrm{2},\:{n}=\mathrm{1} \\ $$$$\mathrm{3}=\sqrt{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+\mathrm{3}\sqrt{\mathrm{1}+\mathrm{4}\sqrt{\mathrm{1}+\mathrm{5}\sqrt{\mathrm{1}+…}}}}} \\ $$
