Question Number 64406 by rajesh4661kumar@gamil.com last updated on 17/Jul/19

Commented by Tony Lin last updated on 17/Jul/19
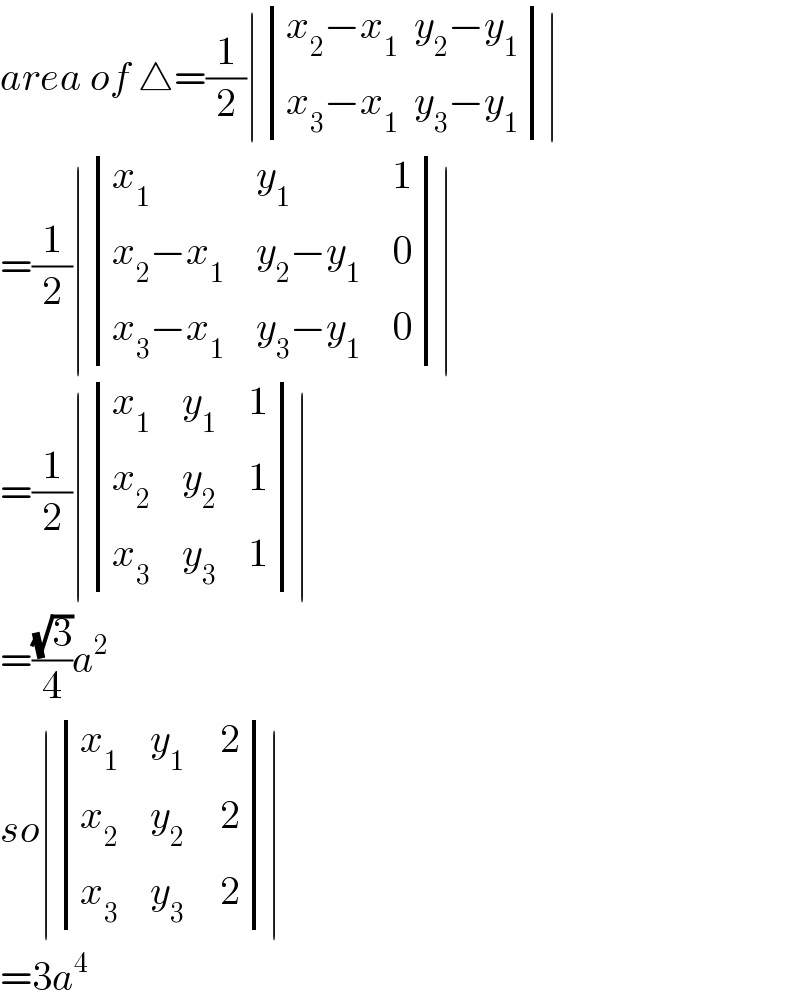
$${area}\:{of}\:\bigtriangleup=\frac{\mathrm{1}}{\mathrm{2}}\mid\begin{vmatrix}{{x}_{\mathrm{2}} −{x}_{\mathrm{1}} \:\:{y}_{\mathrm{2}} −{y}_{\mathrm{1}} }\\{{x}_{\mathrm{3}} −{x}_{\mathrm{1}} \:\:{y}_{\mathrm{3}} −{y}_{\mathrm{1}} }\end{vmatrix}\mid \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mid\begin{vmatrix}{{x}_{\mathrm{1}} }&{{y}_{\mathrm{1}} }&{\mathrm{1}}\\{{x}_{\mathrm{2}} −{x}_{\mathrm{1}} }&{{y}_{\mathrm{2}} −{y}_{\mathrm{1}} }&{\mathrm{0}}\\{{x}_{\mathrm{3}} −{x}_{\mathrm{1}} }&{{y}_{\mathrm{3}} −{y}_{\mathrm{1}} }&{\mathrm{0}}\end{vmatrix}\mid \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mid\begin{vmatrix}{{x}_{\mathrm{1}} }&{{y}_{\mathrm{1}} }&{\mathrm{1}}\\{{x}_{\mathrm{2}} }&{{y}_{\mathrm{2}} }&{\mathrm{1}}\\{{x}_{\mathrm{3}} }&{{y}_{\mathrm{3}} }&{\mathrm{1}}\end{vmatrix}\mid \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{a}^{\mathrm{2}} \\ $$$${so}\mid\begin{vmatrix}{{x}_{\mathrm{1}} }&{{y}_{\mathrm{1}} }&{\mathrm{2}}\\{{x}_{\mathrm{2}} }&{{y}_{\mathrm{2}} }&{\mathrm{2}}\\{{x}_{\mathrm{3}} }&{{y}_{\mathrm{3}\:} }&{\mathrm{2}}\end{vmatrix}\mid \\ $$$$=\mathrm{3}{a}^{\mathrm{4}} \\ $$
