Question Number 64447 by Tawa1 last updated on 18/Jul/19
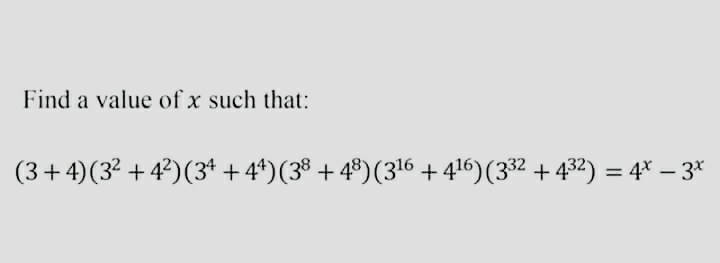
Answered by som(math1967) last updated on 18/Jul/19
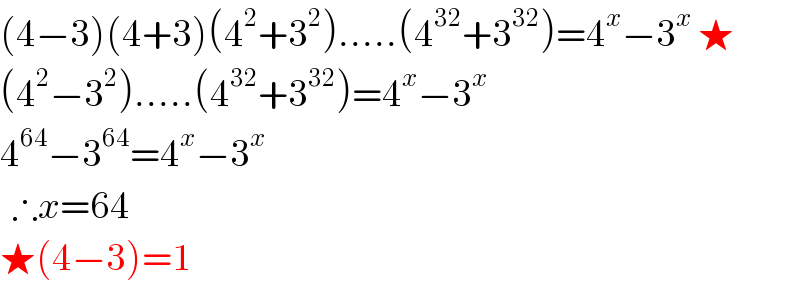
$$\left(\mathrm{4}−\mathrm{3}\right)\left(\mathrm{4}+\mathrm{3}\right)\left(\mathrm{4}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \right)…..\left(\mathrm{4}^{\mathrm{32}} +\mathrm{3}^{\mathrm{32}} \right)=\mathrm{4}^{{x}} −\mathrm{3}^{{x}} \:\bigstar \\ $$$$\left(\mathrm{4}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} \right)…..\left(\mathrm{4}^{\mathrm{32}} +\mathrm{3}^{\mathrm{32}} \right)=\mathrm{4}^{{x}} −\mathrm{3}^{{x}} \\ $$$$\mathrm{4}^{\mathrm{64}} −\mathrm{3}^{\mathrm{64}} =\mathrm{4}^{{x}} −\mathrm{3}^{{x}} \\ $$$$\:\:\therefore{x}=\mathrm{64} \\ $$$$\bigstar\left(\mathrm{4}−\mathrm{3}\right)=\mathrm{1} \\ $$
Commented by Tawa1 last updated on 18/Jul/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by som(math1967) last updated on 18/Jul/19
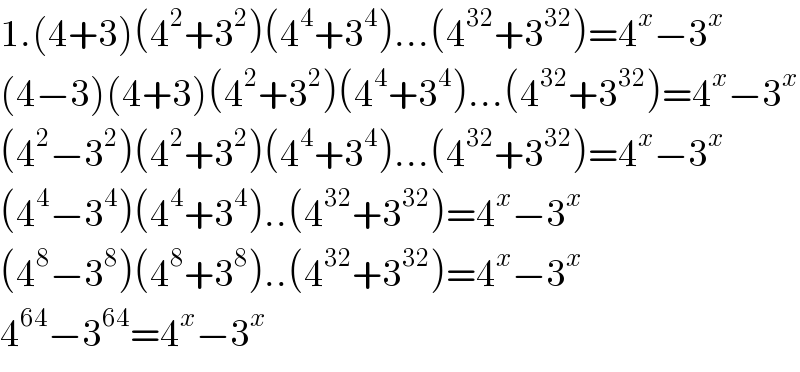
$$\mathrm{1}.\left(\mathrm{4}+\mathrm{3}\right)\left(\mathrm{4}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \right)\left(\mathrm{4}^{\mathrm{4}} +\mathrm{3}^{\mathrm{4}} \right)…\left(\mathrm{4}^{\mathrm{32}} +\mathrm{3}^{\mathrm{32}} \right)=\mathrm{4}^{{x}} −\mathrm{3}^{{x}} \\ $$$$\left(\mathrm{4}−\mathrm{3}\right)\left(\mathrm{4}+\mathrm{3}\right)\left(\mathrm{4}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \right)\left(\mathrm{4}^{\mathrm{4}} +\mathrm{3}^{\mathrm{4}} \right)…\left(\mathrm{4}^{\mathrm{32}} +\mathrm{3}^{\mathrm{32}} \right)=\mathrm{4}^{{x}} −\mathrm{3}^{{x}} \\ $$$$\left(\mathrm{4}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} \right)\left(\mathrm{4}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \right)\left(\mathrm{4}^{\mathrm{4}} +\mathrm{3}^{\mathrm{4}} \right)…\left(\mathrm{4}^{\mathrm{32}} +\mathrm{3}^{\mathrm{32}} \right)=\mathrm{4}^{{x}} −\mathrm{3}^{{x}} \\ $$$$\left(\mathrm{4}^{\mathrm{4}} −\mathrm{3}^{\mathrm{4}} \right)\left(\mathrm{4}^{\mathrm{4}} +\mathrm{3}^{\mathrm{4}} \right)..\left(\mathrm{4}^{\mathrm{32}} +\mathrm{3}^{\mathrm{32}} \right)=\mathrm{4}^{{x}} −\mathrm{3}^{{x}} \\ $$$$\left(\mathrm{4}^{\mathrm{8}} −\mathrm{3}^{\mathrm{8}} \right)\left(\mathrm{4}^{\mathrm{8}} +\mathrm{3}^{\mathrm{8}} \right)..\left(\mathrm{4}^{\mathrm{32}} +\mathrm{3}^{\mathrm{32}} \right)=\mathrm{4}^{{x}} −\mathrm{3}^{{x}} \\ $$$$\mathrm{4}^{\mathrm{64}} −\mathrm{3}^{\mathrm{64}} =\mathrm{4}^{{x}} −\mathrm{3}^{{x}} \\ $$
Commented by Tawa1 last updated on 18/Jul/19
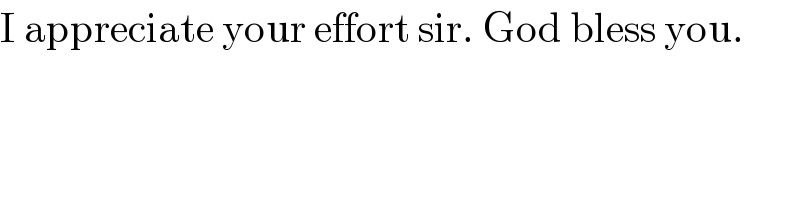
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
