Question-64452

Facebook Tweet Pin

Question Number 64452 by Tanmay chaudhury last updated on 18/Jul/19

Commented by Tanmay chaudhury last updated on 18/Jul/19

$${thank}\:{you}… \\ $$

Commented by Tanmay chaudhury last updated on 18/Jul/19

$${unsolved}\:{problem}… \\ $$

Commented by ajfour last updated on 18/Jul/19

$${i}\:{will}\:{solve}\:{it}\:{by}\:{evening},\:{Tanmay}\:{Sir}.. \\ $$

Commented by mr W last updated on 18/Jul/19

$${could}\:{it}\:{be}\:\mathrm{12}? \\ $$

Commented by Tanmay chaudhury last updated on 18/Jul/19

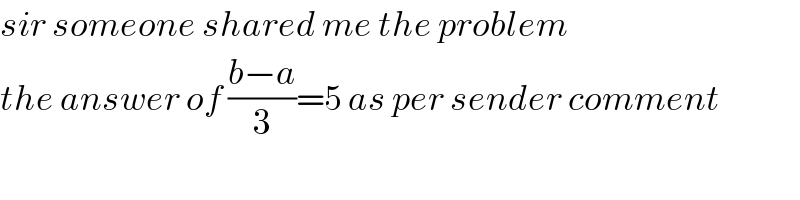
sir someone shared me the problem the answer of ((b−a)/3)=5 as per sender comment

$${sir}\:{someone}\:{shared}\:{me}\:{the}\:{problem} \\ $$$${the}\:{answer}\:{of}\:\frac{{b}−{a}}{\mathrm{3}}=\mathrm{5}\:{as}\:{per}\:{sender}\:{comment} \\ $$

Answered by ajfour last updated on 19/Jul/19

Commented by ajfour last updated on 19/Jul/19

potential within a solid ball of mass M radius R. V(r)=((GMr^3 )/(R^3 (r)))+∫_r ^( R) ((Gρ(4πz^2 )dz)/z) = ((GMr^2 )/R^3 )+((GM(4π))/(((4/3)πR^3 )))(((R^2 −r^2 )/2)) V(r)= ((GM)/R^3 )(((3R^2 −r^2 )/2)) __________________________ gravitational potential energy b/w full ball of radius R , density ρ and the small ball of radius R/2, density −ρ. −∫dU_1 =∫_0 ^( R) ρAVdr =∫_0 ^( R) ρ[2π(r^2 −(r^3 /R))((GM)/R^3 )(((3R^2 −r^2 )/2))dr =((πρGM)/R^3 )∫_0 ^( R) {3R^2 r^2 −r^4 −3Rr^3 +(r^5 /R)}dr = ((3GM^2 )/(4R))(1−(1/5)−(3/4)+(1/6)) U_1 =−((3GM^2 )/(4R))(((13)/(60))) =−((13GM^2 )/(80R)) And gravitational potential energy of small sphere with small sphere be U_2 . U_2 =∫_0 ^( R/2) [V_(R/2) (r)](4πρr^2 )dr U_2 = ∫((G((M/8)))/(((R/2))^3 ))[((3((R/2))^2 −r^2 )/2)](4πρr^2 )dr =((4πGM)/(2R^3 ))(((3M)/(4πR^3 )))∫_0 ^( R/2) (((3R^2 r^2 )/4)−r^4 )dr =((3GM^2 )/(2R))((1/(32))−(1/(5×32))) U_2 =((3GM^2 )/(80R)) W_(reauired) = −(U_1 +U_2 ) = −((GM^2 )/R)(−((13)/(80))+(3/(80))) =((GM^2 )/(8R))

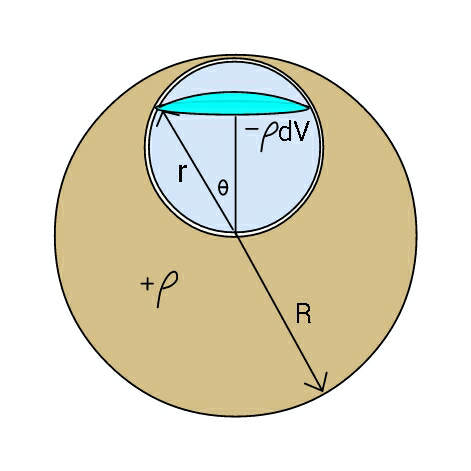
$${potential}\:{within}\:{a}\:{solid}\:{ball}\:{of}\:{mass}\:{M} \\ $$$${radius}\:{R}. \\ $$$${V}\left({r}\right)=\frac{{GMr}^{\mathrm{3}} }{{R}^{\mathrm{3}} \left({r}\right)}+\int_{{r}} ^{\:{R}} \:\frac{{G}\rho\left(\mathrm{4}\pi{z}^{\mathrm{2}} \right){dz}}{{z}} \\ $$$$\:\:\:\:=\:\frac{{GMr}^{\mathrm{2}} }{{R}^{\mathrm{3}} }+\frac{{GM}\left(\mathrm{4}\pi\right)}{\left(\frac{\mathrm{4}}{\mathrm{3}}\pi{R}^{\mathrm{3}} \right)}\left(\frac{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:{V}\left({r}\right)=\:\frac{{GM}}{{R}^{\mathrm{3}} }\left(\frac{\mathrm{3}{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${gravitational}\:{potential}\:{energy} \\ $$$${b}/{w}\:{full}\:{ball}\:{of}\:{radius}\:{R}\:, \\ $$$${density}\:\rho\:{and}\:{the}\:{small}\:{ball}\:{of} \\ $$$${radius}\:{R}/\mathrm{2},\:{density}\:−\rho. \\ $$$$\:\:\:\:\:−\int{dU}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\:{R}} \rho{AVdr} \\ $$$$\:\:=\int_{\mathrm{0}} ^{\:{R}} \rho\left[\mathrm{2}\pi\left({r}^{\mathrm{2}} −\frac{{r}^{\mathrm{3}} }{{R}}\right)\frac{{GM}}{{R}^{\mathrm{3}} }\left(\frac{\mathrm{3}{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }{\mathrm{2}}\right){dr}\right. \\ $$$$\:\:=\frac{\pi\rho{GM}}{{R}^{\mathrm{3}} }\int_{\mathrm{0}} ^{\:{R}} \left\{\mathrm{3}{R}^{\mathrm{2}} {r}^{\mathrm{2}} −{r}^{\mathrm{4}} −\mathrm{3}{Rr}^{\mathrm{3}} +\frac{{r}^{\mathrm{5}} }{{R}}\right\}{dr} \\ $$$$\:=\:\frac{\mathrm{3}{GM}^{\mathrm{2}} }{\mathrm{4}{R}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{6}}\right) \\ $$$$\:\:\:\:{U}_{\mathrm{1}} =−\frac{\mathrm{3}{GM}^{\mathrm{2}} }{\mathrm{4}{R}}\left(\frac{\mathrm{13}}{\mathrm{60}}\right)\:=−\frac{\mathrm{13}{GM}^{\mathrm{2}} }{\mathrm{80}{R}} \\ $$$${And}\:{gravitational}\:{potential}\:{energy} \\ $$$${of}\:{small}\:{sphere}\:{with}\:{small}\:{sphere} \\ $$$${be}\:{U}_{\mathrm{2}} . \\ $$$${U}_{\mathrm{2}} =\int_{\mathrm{0}} ^{\:{R}/\mathrm{2}} \left[{V}_{{R}/\mathrm{2}} \left({r}\right)\right]\left(\mathrm{4}\pi\rho{r}^{\mathrm{2}} \right){dr} \\ $$$$\:{U}_{\mathrm{2}} =\:\int\frac{{G}\left(\frac{{M}}{\mathrm{8}}\right)}{\left(\frac{{R}}{\mathrm{2}}\right)^{\mathrm{3}} }\left[\frac{\mathrm{3}\left(\frac{{R}}{\mathrm{2}}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }{\mathrm{2}}\right]\left(\mathrm{4}\pi\rho{r}^{\mathrm{2}} \right){dr} \\ $$$$\:\:\:=\frac{\mathrm{4}\pi{GM}}{\mathrm{2}{R}^{\mathrm{3}} }\left(\frac{\mathrm{3}{M}}{\mathrm{4}\pi{R}^{\mathrm{3}} }\right)\int_{\mathrm{0}} ^{\:{R}/\mathrm{2}} \left(\frac{\mathrm{3}{R}^{\mathrm{2}} {r}^{\mathrm{2}} }{\mathrm{4}}−{r}^{\mathrm{4}} \right){dr} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3}{GM}^{\mathrm{2}} }{\mathrm{2}{R}}\left(\frac{\mathrm{1}}{\mathrm{32}}−\frac{\mathrm{1}}{\mathrm{5}×\mathrm{32}}\right)\: \\ $$$$\:\:\:\:\:\:\:{U}_{\mathrm{2}} =\frac{\mathrm{3}{GM}^{\mathrm{2}} }{\mathrm{80}{R}} \\ $$$${W}_{{reauired}} =\:−\left({U}_{\mathrm{1}} +{U}_{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:−\frac{{GM}^{\mathrm{2}} }{{R}}\left(−\frac{\mathrm{13}}{\mathrm{80}}+\frac{\mathrm{3}}{\mathrm{80}}\right)\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{{GM}^{\mathrm{2}} }{\mathrm{8}{R}} \\ $$

Commented by Tanmay chaudhury last updated on 19/Jul/19

$${thank}\:{you}\:{sir}\:.. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply