Question Number 64459 by Tawa1 last updated on 18/Jul/19
Commented by Tony Lin last updated on 18/Jul/19
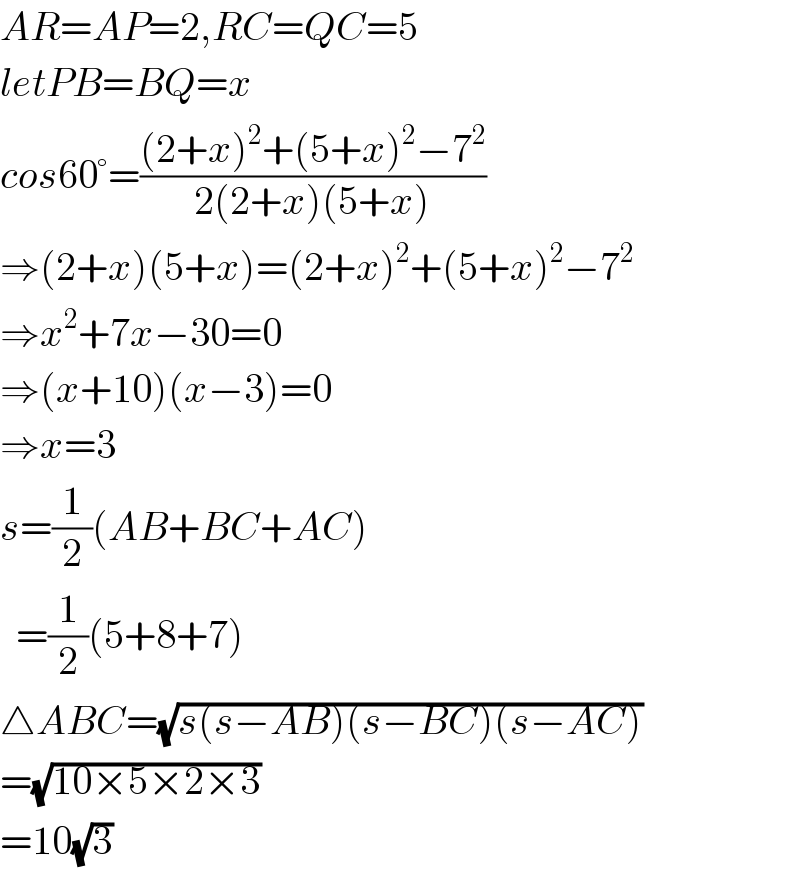
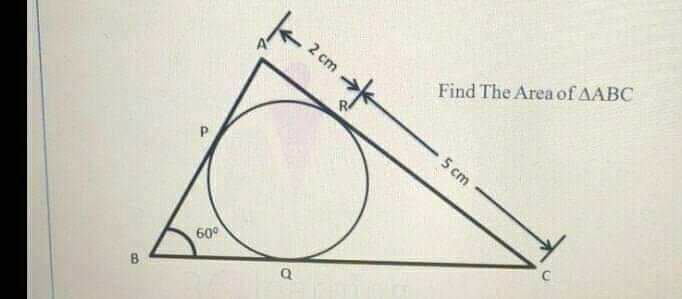
$${AR}={AP}=\mathrm{2},{RC}={QC}=\mathrm{5} \\ $$$${letPB}={BQ}={x} \\ $$$${cos}\mathrm{60}°=\frac{\left(\mathrm{2}+{x}\right)^{\mathrm{2}} +\left(\mathrm{5}+{x}\right)^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{2}+{x}\right)\left(\mathrm{5}+{x}\right)} \\ $$$$\Rightarrow\left(\mathrm{2}+{x}\right)\left(\mathrm{5}+{x}\right)=\left(\mathrm{2}+{x}\right)^{\mathrm{2}} +\left(\mathrm{5}+{x}\right)^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +\mathrm{7}{x}−\mathrm{30}=\mathrm{0} \\ $$$$\Rightarrow\left({x}+\mathrm{10}\right)\left({x}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{3} \\ $$$${s}=\frac{\mathrm{1}}{\mathrm{2}}\left({AB}+{BC}+{AC}\right) \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{5}+\mathrm{8}+\mathrm{7}\right) \\ $$$$\bigtriangleup{ABC}=\sqrt{{s}\left({s}−{AB}\right)\left({s}−{BC}\right)\left({s}−{AC}\right)} \\ $$$$=\sqrt{\mathrm{10}×\mathrm{5}×\mathrm{2}×\mathrm{3}} \\ $$$$=\mathrm{10}\sqrt{\mathrm{3}} \\ $$
Commented by Tawa1 last updated on 18/Jul/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
