Question Number 64478 by necx1 last updated on 18/Jul/19
Commented by necx1 last updated on 18/Jul/19
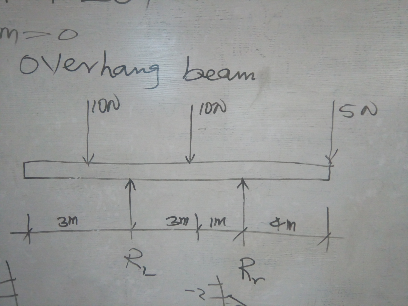
$${please}\:{help}\:{me}\:{analyse}\:{this}\:{free}\:{body} \\ $$$${diagram}.\:{I}'{ll}\:{be}\:{grateful}\:{sirs}. \\ $$
Commented by necx1 last updated on 18/Jul/19
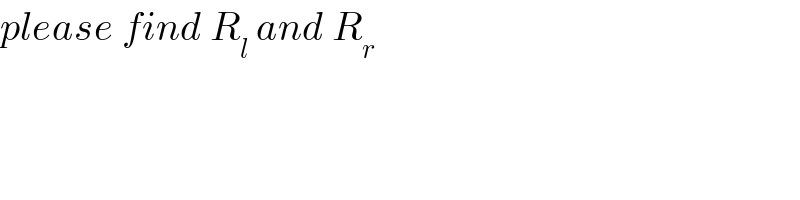
$${please}\:{find}\:{R}_{{l}} \:{and}\:{R}_{{r}} \\ $$
Answered by behi83417@gmail.com last updated on 18/Jul/19

$$\mathrm{R}_{\mathrm{1}} ×\mathrm{8}+\mathrm{R}_{\mathrm{2}} ×\mathrm{4}=\mathrm{10}×?+\mathrm{10}×\mathrm{5} \\ $$$$\mathrm{R}_{\mathrm{1}} +\mathrm{R}_{\mathrm{2}} =\mathrm{10}+\mathrm{10}+\mathrm{5} \\ $$$$\Rightarrow\begin{cases}{\mathrm{2R}_{\mathrm{1}} +\mathrm{R}_{\mathrm{2}} =\mathrm{2}.\mathrm{5}×?+\mathrm{12}.\mathrm{5}}\\{\mathrm{R}_{\mathrm{1}} +\mathrm{R}_{\mathrm{2}} =\mathrm{25}}\end{cases} \\ $$$$\mathrm{R}_{\mathrm{1}} =\mathrm{2}.\mathrm{5}×?−\mathrm{12}.\mathrm{5},\mathrm{R}_{\mathrm{2}} =\mathrm{37}.\mathrm{5}−\mathrm{2}.\mathrm{5}×? \\ $$$$?=\mathrm{distance}\:\mathrm{from}:\:\mathrm{left}\:\mathrm{10}^{\mathrm{N}} \:\mathrm{to}\:\mathrm{5}^{\mathrm{N}} \:\mathrm{force}.\left(\mathrm{not}\:\mathrm{given}\right) \\ $$
Commented by necx1 last updated on 18/Jul/19

$${yes}….{That}'{s}\:{where}\:{i}\:{also}\:{do}\:{not} \\ $$$${understand}.{Though}\:{a}\:{friend}\:{got}\:\mathrm{10}{N} \\ $$$${and}\:\mathrm{15}{N}\:{but}\:{the}\:{process}\:{he}\:{applied}\:{i} \\ $$$${dont}\:{get}.{He}\:{was}\:{using}\:{something} \\ $$$$+{ve}\:{and}\:−{ve}\:{in}\:{relation}\:{to}\:{a}\:{freely} \\ $$$${supported}\:{and}\:{cantilever}\:{beem}.\:{I}\:{also} \\ $$$${think}\:{the}\:{question}\:{is}\:{kinda}\:{not}\:{complete} \\ $$$${in}\:{terms}\:{of}\:{given}\:{parameters}. \\ $$
