Question Number 64516 by Tawa1 last updated on 18/Jul/19
Commented by Tawa1 last updated on 18/Jul/19

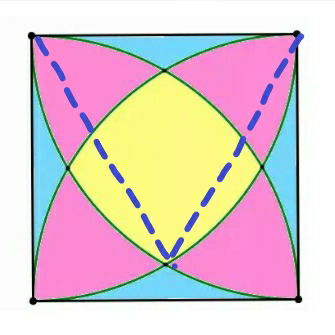
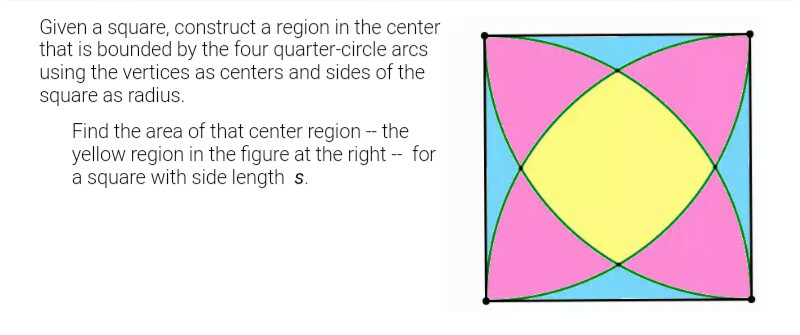
$$\mathrm{Is}\:\mathrm{it}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{find}\:\mathrm{area}\:\mathrm{of}\:\mathrm{each}\:\mathrm{colour}\:? \\ $$$$\mathrm{please}\:\mathrm{help}. \\ $$
Commented by Tawa1 last updated on 18/Jul/19
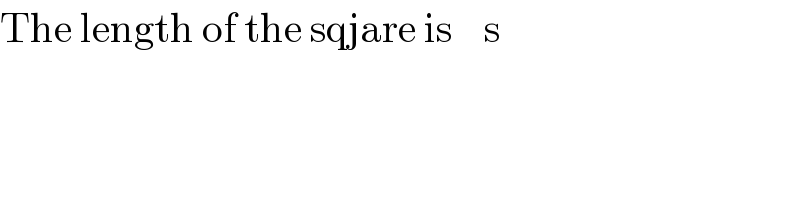
$$\mathrm{The}\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sqjare}\:\mathrm{is}\:\:\:\:\mathrm{s} \\ $$
Commented by Tony Lin last updated on 19/Jul/19

$${blue}\:{area}\left(\mathrm{1}/\mathrm{4}\right) \\ $$$$={square}−\mathrm{2}{sectors}\left(\mathrm{30}°\right)−{equilateral}\:{triangle} \\ $$$$={s}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{\mathrm{3}}{s}^{\mathrm{2}} −\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{s}^{\mathrm{2}} \\ $$$$={s}^{\mathrm{2}} −\frac{\pi}{\mathrm{6}}{s}^{\mathrm{2}} −\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{s}^{\mathrm{2}} \\ $$$${blue}\:{area}=\mathrm{4}{s}^{\mathrm{2}} −\frac{\mathrm{2}\pi}{\mathrm{3}}{s}^{\mathrm{2}} −\sqrt{\mathrm{3}}{s}^{\mathrm{2}} \\ $$$${pink}\:{area}\left(\mathrm{1}/\mathrm{4}\right) \\ $$$$={square}−{sector}\left(\mathrm{90}°\right)−\mathrm{2}{blue}\:{area}\left(\mathrm{1}/\mathrm{4}\right) \\ $$$$={s}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{s}^{\mathrm{2}} ×\frac{\pi}{\mathrm{2}}−\mathrm{2}\left({s}^{\mathrm{2}} −\frac{\pi}{\mathrm{6}}{s}^{\mathrm{2}} −\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{s}^{\mathrm{2}} \right) \\ $$$$=−{s}^{\mathrm{2}} +\frac{\pi}{\mathrm{12}}{s}^{\mathrm{2}} +\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{s}^{\mathrm{2}} \\ $$$${pink}\:{area}=−\mathrm{4}{s}^{\mathrm{2}} +\frac{\pi}{\mathrm{3}}{s}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}{s}^{\mathrm{2}} \\ $$$${yellow}\:{area} \\ $$$$={square}−{blue}\:{area}−{pink}\:{area} \\ $$$$={s}^{\mathrm{2}} −\left(\mathrm{4}{s}^{\mathrm{2}} −\frac{\mathrm{2}\pi}{\mathrm{3}}{s}^{\mathrm{2}} −\sqrt{\mathrm{3}}{s}^{\mathrm{2}} \right)−\left(−\mathrm{4}{s}^{\mathrm{2}} +\frac{\pi}{\mathrm{3}}{s}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}{s}^{\mathrm{2}} \right) \\ $$$$={s}^{\mathrm{2}} +\frac{\pi}{\mathrm{3}}{s}^{\mathrm{2}} −\sqrt{\mathrm{3}}{s}^{\mathrm{2}} \\ $$
Commented by Tawa1 last updated on 19/Jul/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 19/Jul/19
$$\mathrm{Am}\:\mathrm{still}\:\mathrm{studying}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{will}\:\mathrm{let}\:\mathrm{you}\:\mathrm{know}\:\mathrm{when}\:\mathrm{i}\:\mathrm{finish} \\ $$$$\mathrm{studying}\:\mathrm{it}\:\mathrm{sir} \\ $$
Answered by MJS last updated on 18/Jul/19
![let s=2t center of the square = ((0),(0) ) corners A= (((−t)),((−t)) ) B= ((t),((−t)) ) C= ((t),(t) ) D= (((−g)),(t) ) corners of the yellow area circle_(A, 2t) ∩circle_(B, 2t) c_(A, 2t) : (x+t)^2 +(y+t)^2 =4t^2 (i) c_(B, 2t) : (x−t)^2 +(y+t)^2 =4t^2 (ii) (i)−(ii) (x+t)^2 −(x−t)^2 =0 4tx=0 ⇒ x=0 [because t≠0] (i) with x=0 t^2 +(y+t)^2 =4t^2 ⇒ y=(−1±(√3))t [but we need the upper intersection] ⇒ y=(−1+(√3))t ⇒ corners of the yellow area E= ((0),(((1−(√3))t)) ) F= ((((−1+(√3))t)),(0) ) G= ((0),(((−1+(√3))t)) ) H= ((((1−(√3))t)),(0) ) the yellow area 4∫_((1−(√3))t) ^0 c_(B, 2t) dx c_(B, 2t) : y=−t+(√((t+x)(3t−x))) 4∫_((1−(√3))t) ^0 (−t+(√((t+x)(3t−x))))dx=4(1−(√3)+(π/3))t^2 the blue area 8∫_(−t) ^0 (t−c_(A, 2t) )dx c_(A, 2t) : y=−t+(√((t−x)(3t+x))) 8∫_(−t) ^0 (2t−(√((t−x)(3t+x))))dx=4(4−(√3)−((2π)/3))t^2 the pink area = square−(yellow+blue) 4t^2 −(4(1−(√3)+(π/3))t^2 +4(4−(√3)−((2π)/3))t^2 )= =4(−4+2(√3)+(π/3))t^2 with t=(s/2) we get yellow =(1−(√3)+(π/3))s^2 ≈.315147s^2 blue =(4−(√3)−((2π)/3))s^2 ≈.173554s^2 pink =(−4+2(√3)+(π/3))s^2 ≈.511299s^2](https://www.tinkutara.com/question/Q64521.png)
$$\mathrm{let}\:{s}=\mathrm{2}{t} \\ $$$$\mathrm{center}\:\mathrm{of}\:\mathrm{the}\:\mathrm{square}\:=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix} \\ $$$$\mathrm{corners}\:{A}=\begin{pmatrix}{−{t}}\\{−{t}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{{t}}\\{−{t}}\end{pmatrix}\:\:{C}=\begin{pmatrix}{{t}}\\{{t}}\end{pmatrix}\:\:{D}=\begin{pmatrix}{−{g}}\\{{t}}\end{pmatrix} \\ $$$$\mathrm{corners}\:\mathrm{of}\:\mathrm{the}\:\mathrm{yellow}\:\mathrm{area} \\ $$$$\mathrm{circle}_{{A},\:\mathrm{2}{t}} \cap\mathrm{circle}_{{B},\:\mathrm{2}{t}} \\ $$$$\mathrm{c}_{{A},\:\mathrm{2}{t}} :\:\left({x}+{t}\right)^{\mathrm{2}} +\left({y}+{t}\right)^{\mathrm{2}} =\mathrm{4}{t}^{\mathrm{2}} \:\:\left(\mathrm{i}\right) \\ $$$$\mathrm{c}_{{B},\:\mathrm{2}{t}} :\:\left({x}−{t}\right)^{\mathrm{2}} +\left({y}+{t}\right)^{\mathrm{2}} =\mathrm{4}{t}^{\mathrm{2}} \:\:\left(\mathrm{ii}\right) \\ $$$$\left(\mathrm{i}\right)−\left(\mathrm{ii}\right) \\ $$$$\left({x}+{t}\right)^{\mathrm{2}} −\left({x}−{t}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{4}{tx}=\mathrm{0}\:\Rightarrow\:{x}=\mathrm{0}\:\left[\mathrm{because}\:{t}\neq\mathrm{0}\right] \\ $$$$\left(\mathrm{i}\right)\:\mathrm{with}\:{x}=\mathrm{0} \\ $$$${t}^{\mathrm{2}} +\left({y}+{t}\right)^{\mathrm{2}} =\mathrm{4}{t}^{\mathrm{2}} \\ $$$$\Rightarrow\:{y}=\left(−\mathrm{1}\pm\sqrt{\mathrm{3}}\right){t}\:\left[\mathrm{but}\:\mathrm{we}\:\mathrm{need}\:\mathrm{the}\:\mathrm{upper}\right. \\ $$$$\left.\:\:\:\:\:\mathrm{intersection}\right] \\ $$$$\Rightarrow\:{y}=\left(−\mathrm{1}+\sqrt{\mathrm{3}}\right){t} \\ $$$$\Rightarrow\:\mathrm{corners}\:\mathrm{of}\:\mathrm{the}\:\mathrm{yellow}\:\mathrm{area} \\ $$$${E}=\begin{pmatrix}{\mathrm{0}}\\{\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}}\end{pmatrix}\:\:{F}=\begin{pmatrix}{\left(−\mathrm{1}+\sqrt{\mathrm{3}}\right){t}}\\{\mathrm{0}}\end{pmatrix}\:\:{G}=\begin{pmatrix}{\mathrm{0}}\\{\left(−\mathrm{1}+\sqrt{\mathrm{3}}\right){t}}\end{pmatrix}\:\:{H}=\begin{pmatrix}{\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}}\\{\mathrm{0}}\end{pmatrix} \\ $$$$\mathrm{the}\:\mathrm{yellow}\:\mathrm{area} \\ $$$$\mathrm{4}\underset{\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}} {\overset{\mathrm{0}} {\int}}\mathrm{c}_{{B},\:\mathrm{2}{t}} {dx} \\ $$$$\mathrm{c}_{{B},\:\mathrm{2}{t}} :\:{y}=−{t}+\sqrt{\left({t}+{x}\right)\left(\mathrm{3}{t}−{x}\right)} \\ $$$$\mathrm{4}\underset{\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}} {\overset{\mathrm{0}} {\int}}\left(−{t}+\sqrt{\left({t}+{x}\right)\left(\mathrm{3}{t}−{x}\right)}\right){dx}=\mathrm{4}\left(\mathrm{1}−\sqrt{\mathrm{3}}+\frac{\pi}{\mathrm{3}}\right){t}^{\mathrm{2}} \\ $$$$\mathrm{the}\:\mathrm{blue}\:\mathrm{area} \\ $$$$\mathrm{8}\underset{−{t}} {\overset{\mathrm{0}} {\int}}\left({t}−\mathrm{c}_{{A},\:\mathrm{2}{t}} \right){dx} \\ $$$$\mathrm{c}_{{A},\:\mathrm{2}{t}} :\:{y}=−{t}+\sqrt{\left({t}−{x}\right)\left(\mathrm{3}{t}+{x}\right)} \\ $$$$\mathrm{8}\underset{−{t}} {\overset{\mathrm{0}} {\int}}\left(\mathrm{2}{t}−\sqrt{\left({t}−{x}\right)\left(\mathrm{3}{t}+{x}\right)}\right){dx}=\mathrm{4}\left(\mathrm{4}−\sqrt{\mathrm{3}}−\frac{\mathrm{2}\pi}{\mathrm{3}}\right){t}^{\mathrm{2}} \\ $$$$\mathrm{the}\:\mathrm{pink}\:\mathrm{area}\:=\:\mathrm{square}−\left(\mathrm{yellow}+\mathrm{blue}\right) \\ $$$$\mathrm{4t}^{\mathrm{2}} −\left(\mathrm{4}\left(\mathrm{1}−\sqrt{\mathrm{3}}+\frac{\pi}{\mathrm{3}}\right){t}^{\mathrm{2}} +\mathrm{4}\left(\mathrm{4}−\sqrt{\mathrm{3}}−\frac{\mathrm{2}\pi}{\mathrm{3}}\right){t}^{\mathrm{2}} \right)= \\ $$$$=\mathrm{4}\left(−\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}+\frac{\pi}{\mathrm{3}}\right){t}^{\mathrm{2}} \\ $$$$\mathrm{with}\:{t}=\frac{{s}}{\mathrm{2}}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{yellow}\:=\left(\mathrm{1}−\sqrt{\mathrm{3}}+\frac{\pi}{\mathrm{3}}\right){s}^{\mathrm{2}} \approx.\mathrm{315147}{s}^{\mathrm{2}} \\ $$$$\mathrm{blue}\:=\left(\mathrm{4}−\sqrt{\mathrm{3}}−\frac{\mathrm{2}\pi}{\mathrm{3}}\right){s}^{\mathrm{2}} \approx.\mathrm{173554}{s}^{\mathrm{2}} \\ $$$$\mathrm{pink}\:=\left(−\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}+\frac{\pi}{\mathrm{3}}\right){s}^{\mathrm{2}} \approx.\mathrm{511299}{s}^{\mathrm{2}} \\ $$
Commented by Tawa1 last updated on 19/Jul/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{will}\:\mathrm{study}\:\mathrm{it}\:\mathrm{and}\:\mathrm{get}\:\mathrm{back}\:\mathrm{to}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{ifi} \\ $$$$\mathrm{i}\:\mathrm{get}\:\mathrm{issue}\:\mathrm{in}\:\mathrm{the}\:\mathrm{workings}. \\ $$
Commented by Tawa1 last updated on 19/Jul/19

$$\mathrm{why}\:\mathrm{is}\:\:\:\mathrm{s}\:=\:\mathrm{2t}\:\mathrm{sir}\:?\:\:\mathrm{and}\:\mathrm{how}\:\mathrm{we}\:\mathrm{get}\:\mathrm{corners} \\ $$$$\mathrm{and}\:\mathrm{what}\:\mathrm{is}\:\mathrm{corner}\:\mathrm{A},\:\mathrm{2t}.\:\:\:\:\:\mathrm{Sorry}\:\mathrm{sir}\:\mathrm{if}\:\mathrm{my}\:\mathrm{questions}\:\mathrm{is}\:\mathrm{too}\:\mathrm{much}. \\ $$$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Commented by MJS last updated on 19/Jul/19

$$\mathrm{corners}=\mathrm{vertices} \\ $$$$\mathrm{sorry}\:\mathrm{my}\:\mathrm{native}\:\mathrm{language}\:\mathrm{is}\:\mathrm{German}\:\mathrm{so}\:\mathrm{it}'\mathrm{s} \\ $$$$\mathrm{just}\:\mathrm{a}\:\mathrm{translation}\:\mathrm{error} \\ $$$$\mathrm{c}_{{A},\:\mathrm{2}{t}} \:\mathrm{means}\:\mathrm{circle}\:\mathrm{with}\:\mathrm{center}\:{A}\:\mathrm{and}\:\mathrm{radius}\:\mathrm{2}{t} \\ $$$$\mathrm{I}\:\mathrm{put}\:{s}=\mathrm{2}{t}\:\mathrm{to}\:\mathrm{avoid}\:\mathrm{fractions}\:\mathrm{in}\:\mathrm{the}\:\mathrm{coordinates} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{vertices}\:\mathrm{like}\:{A}=\begin{pmatrix}{−\frac{{s}}{\mathrm{2}}}\\{−\frac{{s}}{\mathrm{2}}}\end{pmatrix}\:\:\mathrm{and}\:\mathrm{the} \\ $$$$\mathrm{equations}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circles}\:\mathrm{like}\:\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$
Commented by Tawa1 last updated on 19/Jul/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{more}\:\mathrm{sir}. \\ $$$$\mathrm{Am}\:\mathrm{still}\:\mathrm{studying}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{sir}.\:\:\mathrm{I}\:\mathrm{will}\:\mathrm{let}\:\mathrm{you}\:\mathrm{know}\:\mathrm{when}\:\mathrm{i}\:\mathrm{finished} \\ $$$$\mathrm{it}.\:\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{want}\:\mathrm{to}\:\mathrm{ask}\:\mathrm{questions}\:\mathrm{now}\:\mathrm{untill}\:\mathrm{i}\:\mathrm{understand}\:\mathrm{everything} \\ $$$$\mathrm{on}\:\mathrm{my}\:\mathrm{own}.\:\:\mathrm{I}\:\mathrm{will}\:\mathrm{tell}\:\mathrm{you}\:\mathrm{when}\:\mathrm{am}\:\mathrm{through}. \\ $$
Answered by Tony Lin last updated on 23/Jul/19