Question Number 64564 by Tawa1 last updated on 19/Jul/19

Commented by Tony Lin last updated on 19/Jul/19

$${let}\:{cosx}={t} \\ $$$$\frac{{t}}{\mathrm{1}+\frac{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{{t}}}−\frac{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\mathrm{1}+{t}} \\ $$$$=\frac{{t}^{\mathrm{2}} }{\mathrm{1}+\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}−\frac{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\mathrm{1}+{t}} \\ $$$$=\mathrm{1}−\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }−\frac{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\mathrm{1}+{t}}\neq{t}−\sqrt{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$${if}\:\mathrm{1}−\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }−\frac{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\mathrm{1}+{t}}={t}−\sqrt{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{1}−\frac{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\mathrm{1}+{t}}={t} \\ $$$$\Rightarrow\mathrm{1}−{t}=\frac{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\mathrm{1}+{t}} \\ $$$$\Rightarrow\mathrm{1}−{t}^{\mathrm{2}} =\sqrt{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$\Rightarrow{t}=\:\mathrm{1}{or}\:\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{2}{k}\pi,\:{k}\in{Z} \\ $$$$\Rightarrow{x}=\frac{\pi}{\mathrm{2}}+{k}\pi\left({impossible},\:{tanx}\:{has}\:{no}\:{value}\right) \\ $$
Commented by MJS last updated on 19/Jul/19
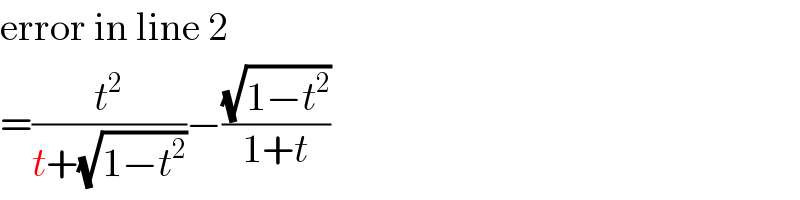
$$\mathrm{error}\:\mathrm{in}\:\mathrm{line}\:\mathrm{2} \\ $$$$=\frac{{t}^{\mathrm{2}} }{{t}+\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}−\frac{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\mathrm{1}+{t}} \\ $$
