Question-64775

Question Number 64775 by Rio Michael last updated on 21/Jul/19

Commented by Rio Michael last updated on 21/Jul/19

the figure above shows a string PQRS , P and S are attached to a fixed support and mass ,m, and 2.5 kg are attached at the points Q and R respectively and the system is in equilibruim. Calculate a) the mass,m. b) the tension T. c)the angle θ (represented as ∅ on the diagram)

$${the}\:{figure}\:{above}\:{shows}\:{a}\:{string}\:{PQRS}\:,\:{P}\:{and}\:{S}\:{are}\:{attached}\:{to}\:{a}\:{fixed}\:{support}\:{and} \\ $$$${mass}\:,{m},\:{and}\:\mathrm{2}.\mathrm{5}\:\mathrm{kg}\:{are}\:{attached}\:{at}\:{the}\:{points}\:{Q}\:{and}\:{R}\:{respectively}\:{and}\:{the}\:{system} \\ $$$${is}\:{in}\:{equilibruim}.\:{Calculate} \\ $$$$\left.{a}\right)\:{the}\:{mass},{m}. \\ $$$$\left.{b}\right)\:{the}\:{tension}\:{T}. \\ $$$$\left.{c}\right){the}\:{angle}\:\theta\:\left({represented}\:{as}\:\varnothing\:{on}\:{the}\:{diagram}\right) \\ $$

Answered by behi83417@gmail.com last updated on 21/Jul/19

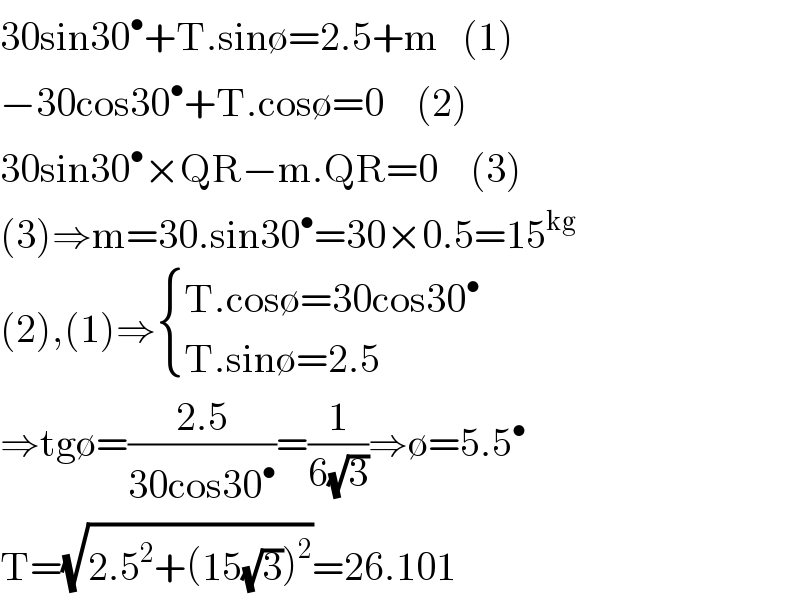
30sin30^• +T.sin∅=2.5+m (1) −30cos30^• +T.cos∅=0 (2) 30sin30^• ×QR−m.QR=0 (3) (3)⇒m=30.sin30^• =30×0.5=15^(kg) (2),(1)⇒ { ((T.cos∅=30cos30^• )),((T.sin∅=2.5)) :} ⇒tg∅=((2.5)/(30cos30^• ))=(1/(6(√3)))⇒∅=5.5^• T=(√(2.5^2 +(15(√3))^2 ))=26.101

$$\mathrm{30sin30}^{\bullet} +\mathrm{T}.\mathrm{sin}\emptyset=\mathrm{2}.\mathrm{5}+\mathrm{m}\:\:\:\left(\mathrm{1}\right) \\ $$$$−\mathrm{30cos30}^{\bullet} +\mathrm{T}.\mathrm{cos}\emptyset=\mathrm{0}\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\mathrm{30sin30}^{\bullet} ×\mathrm{QR}−\mathrm{m}.\mathrm{QR}=\mathrm{0}\:\:\:\:\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{3}\right)\Rightarrow\mathrm{m}=\mathrm{30}.\mathrm{sin30}^{\bullet} =\mathrm{30}×\mathrm{0}.\mathrm{5}=\mathrm{15}^{\mathrm{kg}} \\ $$$$\left(\mathrm{2}\right),\left(\mathrm{1}\right)\Rightarrow\begin{cases}{\mathrm{T}.\mathrm{cos}\emptyset=\mathrm{30cos30}^{\bullet} }\\{\mathrm{T}.\mathrm{sin}\emptyset=\mathrm{2}.\mathrm{5}}\end{cases} \\ $$$$\Rightarrow\mathrm{tg}\emptyset=\frac{\mathrm{2}.\mathrm{5}}{\mathrm{30cos30}^{\bullet} }=\frac{\mathrm{1}}{\mathrm{6}\sqrt{\mathrm{3}}}\Rightarrow\emptyset=\mathrm{5}.\mathrm{5}^{\bullet} \\ $$$$\mathrm{T}=\sqrt{\mathrm{2}.\mathrm{5}^{\mathrm{2}} +\left(\mathrm{15}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }=\mathrm{26}.\mathrm{101} \\ $$

Commented by Rio Michael last updated on 21/Jul/19

$${excuse}\:{me}\:{sir},\:{it}'{s}\:\mathrm{60}° \\ $$

Commented by Rio Michael last updated on 21/Jul/19

$${but}\:{thanks}\:{sir} \\ $$

Commented by Rio Michael last updated on 22/Jul/19

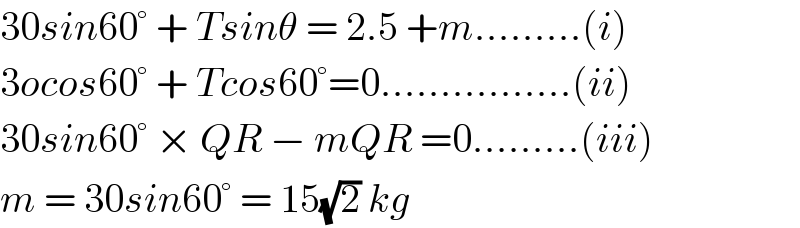
30sin60° + Tsinθ = 2.5 +m.........(i) 3ocos60° + Tcos60°=0................(ii) 30sin60° × QR − mQR =0.........(iii) m = 30sin60° = 15(√2) kg

$$\mathrm{30}{sin}\mathrm{60}°\:+\:{Tsin}\theta\:=\:\mathrm{2}.\mathrm{5}\:+{m}………\left({i}\right) \\ $$$$\mathrm{3}{ocos}\mathrm{60}°\:+\:{Tcos}\mathrm{60}°=\mathrm{0}…………….\left({ii}\right) \\ $$$$\mathrm{30}{sin}\mathrm{60}°\:×\:{QR}\:−\:{mQR}\:=\mathrm{0}………\left({iii}\right) \\ $$$${m}\:=\:\mathrm{30}{sin}\mathrm{60}°\:=\:\mathrm{15}\sqrt{\mathrm{2}}\:{kg} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply