Question Number 64785 by Rio Michael last updated on 21/Jul/19

Answered by LPM last updated on 21/Jul/19
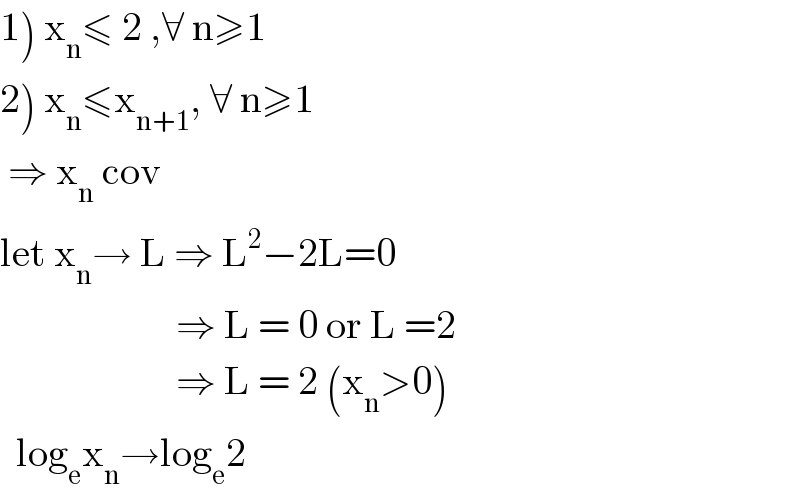
$$\left.\mathrm{1}\right)\:\mathrm{x}_{\mathrm{n}} \leqslant\:\mathrm{2}\:,\forall\:\mathrm{n}\geqslant\mathrm{1} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{x}_{\mathrm{n}} \leqslant\mathrm{x}_{\mathrm{n}+\mathrm{1}} ,\:\forall\:\mathrm{n}\geqslant\mathrm{1} \\ $$$$\:\Rightarrow\:\mathrm{x}_{\mathrm{n}} \:\mathrm{cov} \\ $$$$\mathrm{let}\:\mathrm{x}_{\mathrm{n}} \rightarrow\:\mathrm{L}\:\Rightarrow\:\mathrm{L}^{\mathrm{2}} −\mathrm{2L}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\mathrm{L}\:=\:\mathrm{0}\:\mathrm{or}\:\mathrm{L}\:=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\mathrm{L}\:=\:\mathrm{2}\:\left(\mathrm{x}_{\mathrm{n}} >\mathrm{0}\right) \\ $$$$\:\:\mathrm{log}_{\mathrm{e}} \mathrm{x}_{\mathrm{n}} \rightarrow\mathrm{log}_{\mathrm{e}} \mathrm{2} \\ $$
