Question Number 64887 by ajfour last updated on 22/Jul/19

Answered by mr W last updated on 22/Jul/19
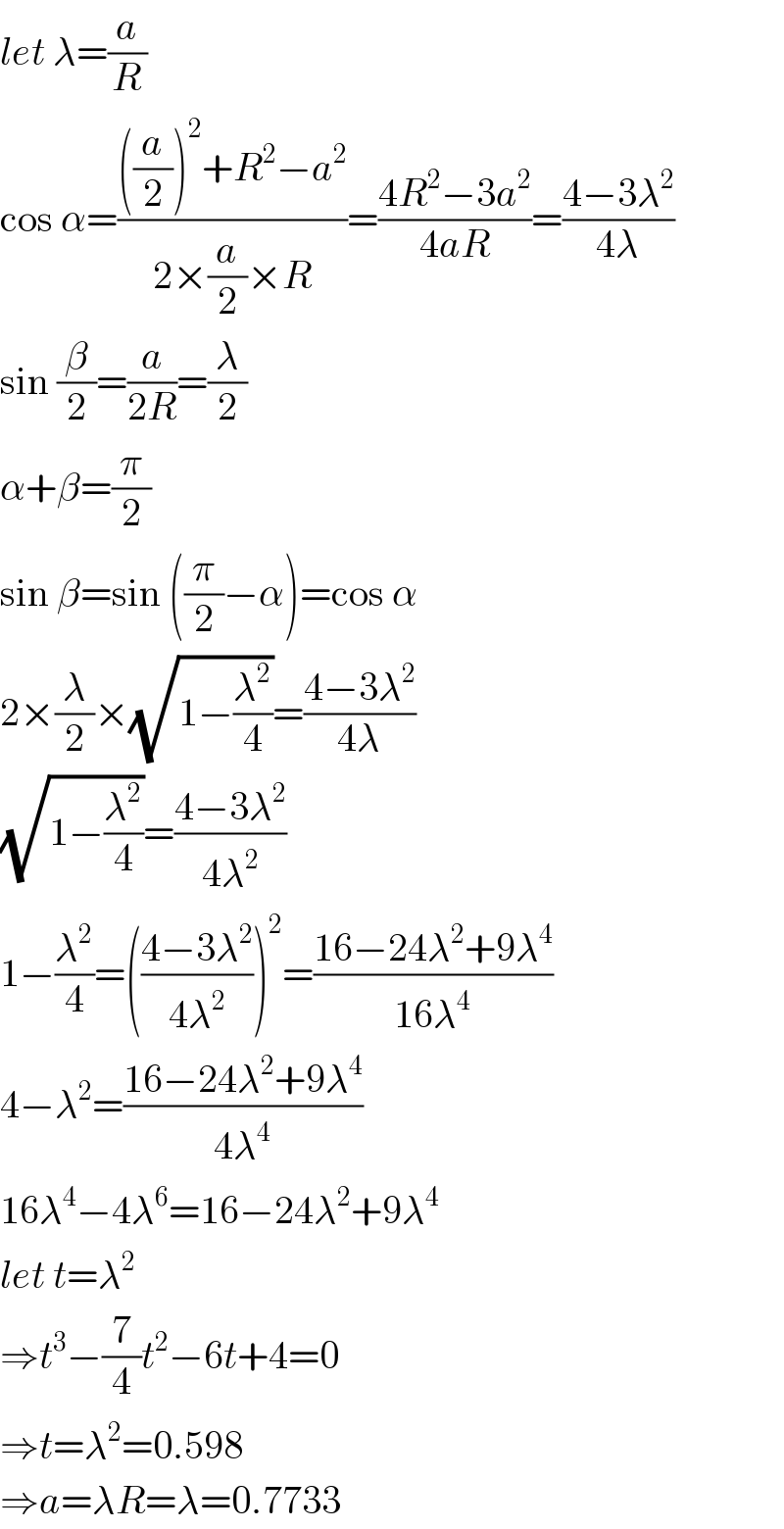
$${let}\:\lambda=\frac{{a}}{{R}} \\ $$$$\mathrm{cos}\:\alpha=\frac{\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}×\frac{{a}}{\mathrm{2}}×{R}}=\frac{\mathrm{4}{R}^{\mathrm{2}} −\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{4}{aR}}=\frac{\mathrm{4}−\mathrm{3}\lambda^{\mathrm{2}} }{\mathrm{4}\lambda} \\ $$$$\mathrm{sin}\:\frac{\beta}{\mathrm{2}}=\frac{{a}}{\mathrm{2}{R}}=\frac{\lambda}{\mathrm{2}} \\ $$$$\alpha+\beta=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\beta=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\alpha\right)=\mathrm{cos}\:\alpha \\ $$$$\mathrm{2}×\frac{\lambda}{\mathrm{2}}×\sqrt{\mathrm{1}−\frac{\lambda^{\mathrm{2}} }{\mathrm{4}}}=\frac{\mathrm{4}−\mathrm{3}\lambda^{\mathrm{2}} }{\mathrm{4}\lambda} \\ $$$$\sqrt{\mathrm{1}−\frac{\lambda^{\mathrm{2}} }{\mathrm{4}}}=\frac{\mathrm{4}−\mathrm{3}\lambda^{\mathrm{2}} }{\mathrm{4}\lambda^{\mathrm{2}} } \\ $$$$\mathrm{1}−\frac{\lambda^{\mathrm{2}} }{\mathrm{4}}=\left(\frac{\mathrm{4}−\mathrm{3}\lambda^{\mathrm{2}} }{\mathrm{4}\lambda^{\mathrm{2}} }\right)^{\mathrm{2}} =\frac{\mathrm{16}−\mathrm{24}\lambda^{\mathrm{2}} +\mathrm{9}\lambda^{\mathrm{4}} }{\mathrm{16}\lambda^{\mathrm{4}} } \\ $$$$\mathrm{4}−\lambda^{\mathrm{2}} =\frac{\mathrm{16}−\mathrm{24}\lambda^{\mathrm{2}} +\mathrm{9}\lambda^{\mathrm{4}} }{\mathrm{4}\lambda^{\mathrm{4}} } \\ $$$$\mathrm{16}\lambda^{\mathrm{4}} −\mathrm{4}\lambda^{\mathrm{6}} =\mathrm{16}−\mathrm{24}\lambda^{\mathrm{2}} +\mathrm{9}\lambda^{\mathrm{4}} \\ $$$${let}\:{t}=\lambda^{\mathrm{2}} \\ $$$$\Rightarrow{t}^{\mathrm{3}} −\frac{\mathrm{7}}{\mathrm{4}}{t}^{\mathrm{2}} −\mathrm{6}{t}+\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow{t}=\lambda^{\mathrm{2}} =\mathrm{0}.\mathrm{598} \\ $$$$\Rightarrow{a}=\lambda{R}=\lambda=\mathrm{0}.\mathrm{7733} \\ $$
Commented by ajfour last updated on 23/Jul/19
$${Thanks}\:{sir},\:{very}\:{pragmatic}! \\ $$
