Question-64916

Question Number 64916 by Masumsiddiqui399@gmail.com last updated on 23/Jul/19

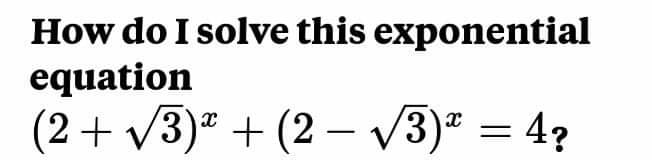
Commented by Tawa1 last updated on 23/Jul/19

(2 + (√3))^x + ((1/(2 + (√3))))^x = 4 [since 2 − (√3) = (1/(2 + (√3))) on rationalise] (2 + (√3))^x + (1/((2 + (√3))^x )) = 4 Let (2 + (√3))^x = y y + (1/y) = 4 y^2 + 1 = 4y y^2 − 4y + 1 = 0 a = 1, b = − 4, c = 1 ⇒ y = ((− (− 4) ± (√((− 4)^2 − 4(1)(1))))/(2(1))) ⇒ y = ((4 ± (√(16− 4)))/2) ⇒ y = ((4 ± (√(12)))/2) ⇒ y = ((4 ± (√(4 × 3)))/2) ⇒ y = ((4 ± 2(√3))/2) ⇒ y = 2 ± (√3) ⇒ y = 2 + (√3) or y = 2 − (√3) Recall the Let (2 + (√3))^x = y ⇒ (2 + (√3))^x = (2 + (√3))^1 Base are the same: ⇒ x = 1 Or (2 + (√3))^x = (2 − (√3))^1 (2 + (√3))^x = (1/(2 + (√3))) (2 + (√3))^x = (2 + (√3))^(−1) Base are the same: ⇒ x = − 1 Finally x = 1 or x = − 1

$$\left(\mathrm{2}\:+\:\sqrt{\mathrm{3}}\right)^{\mathrm{x}} \:+\:\left(\frac{\mathrm{1}}{\mathrm{2}\:+\:\sqrt{\mathrm{3}}}\right)^{\mathrm{x}} \:=\:\:\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\mathrm{since}\:\:\:\:\mathrm{2}\:−\:\sqrt{\mathrm{3}}\:\:=\:\:\frac{\mathrm{1}}{\mathrm{2}\:+\:\sqrt{\mathrm{3}}}\:\:\mathrm{on}\:\mathrm{rationalise}\right] \\ $$$$\left(\mathrm{2}\:+\:\sqrt{\mathrm{3}}\right)^{\mathrm{x}} \:+\:\frac{\mathrm{1}}{\left(\mathrm{2}\:+\:\sqrt{\mathrm{3}}\right)^{\mathrm{x}} }\:=\:\:\mathrm{4} \\ $$$$\mathrm{Let}\:\:\:\:\:\left(\mathrm{2}\:+\:\sqrt{\mathrm{3}}\right)^{\mathrm{x}} \:\:=\:\:\mathrm{y} \\ $$$$\:\:\:\mathrm{y}\:+\:\frac{\mathrm{1}}{\mathrm{y}}\:=\:\:\mathrm{4} \\ $$$$\:\:\:\mathrm{y}^{\mathrm{2}} \:+\:\mathrm{1}\:=\:\:\mathrm{4y} \\ $$$$\:\:\:\mathrm{y}^{\mathrm{2}} \:−\:\mathrm{4y}\:+\:\mathrm{1}\:\:\:=\:\:\mathrm{0} \\ $$$$\mathrm{a}\:=\:\mathrm{1},\:\mathrm{b}\:=\:−\:\mathrm{4},\:\mathrm{c}\:=\:\mathrm{1} \\ $$$$\:\:\:\Rightarrow\:\:\mathrm{y}\:\:=\:\:\:\frac{−\:\left(−\:\mathrm{4}\right)\:\pm\:\sqrt{\left(−\:\mathrm{4}\right)^{\mathrm{2}} \:−\:\mathrm{4}\left(\mathrm{1}\right)\left(\mathrm{1}\right)}}{\mathrm{2}\left(\mathrm{1}\right)} \\ $$$$\:\:\:\Rightarrow\:\:\mathrm{y}\:\:=\:\:\:\frac{\mathrm{4}\:\pm\:\sqrt{\mathrm{16}−\:\mathrm{4}}}{\mathrm{2}} \\ $$$$\:\:\:\Rightarrow\:\:\mathrm{y}\:\:=\:\:\:\frac{\mathrm{4}\:\pm\:\sqrt{\mathrm{12}}}{\mathrm{2}} \\ $$$$\:\:\:\Rightarrow\:\:\mathrm{y}\:\:=\:\:\:\frac{\mathrm{4}\:\pm\:\sqrt{\mathrm{4}\:×\:\mathrm{3}}}{\mathrm{2}} \\ $$$$\:\:\:\Rightarrow\:\:\mathrm{y}\:\:=\:\:\:\frac{\mathrm{4}\:\pm\:\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\:\:\:\Rightarrow\:\:\mathrm{y}\:\:=\:\:\:\mathrm{2}\:\pm\:\sqrt{\mathrm{3}} \\ $$$$\:\:\:\Rightarrow\:\:\mathrm{y}\:\:=\:\:\:\mathrm{2}\:+\:\sqrt{\mathrm{3}}\:\:\:\:\mathrm{or}\:\:\:\mathrm{y}\:\:=\:\:\mathrm{2}\:−\:\sqrt{\mathrm{3}} \\ $$$$\mathrm{Recall}\:\mathrm{the} \\ $$$$\mathrm{Let}\:\:\:\:\:\left(\mathrm{2}\:+\:\sqrt{\mathrm{3}}\right)^{\mathrm{x}} \:\:=\:\:\mathrm{y} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\left(\mathrm{2}\:+\:\sqrt{\mathrm{3}}\right)^{\mathrm{x}} \:\:=\:\:\left(\mathrm{2}\:+\:\sqrt{\mathrm{3}}\right)^{\mathrm{1}} \\ $$$$\mathrm{Base}\:\mathrm{are}\:\mathrm{the}\:\mathrm{same}:\:\:\:\:\:\Rightarrow\:\:\:\:\:\:\:\mathrm{x}\:=\:\mathrm{1} \\ $$$$\mathrm{Or} \\ $$$$\:\:\:\:\:\left(\mathrm{2}\:+\:\sqrt{\mathrm{3}}\right)^{\mathrm{x}} \:\:=\:\:\left(\mathrm{2}\:−\:\sqrt{\mathrm{3}}\right)^{\mathrm{1}} \\ $$$$\:\:\:\:\:\left(\mathrm{2}\:+\:\sqrt{\mathrm{3}}\right)^{\mathrm{x}} \:\:=\:\:\frac{\mathrm{1}}{\mathrm{2}\:+\:\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:\:\left(\mathrm{2}\:+\:\sqrt{\mathrm{3}}\right)^{\mathrm{x}} \:\:=\:\:\left(\mathrm{2}\:+\:\sqrt{\mathrm{3}}\right)^{−\mathrm{1}} \\ $$$$\mathrm{Base}\:\mathrm{are}\:\mathrm{the}\:\mathrm{same}:\:\:\:\:\:\Rightarrow\:\:\:\:\:\:\:\mathrm{x}\:=\:−\:\mathrm{1} \\ $$$$\mathrm{Finally} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}\:\:=\:\:\mathrm{1}\:\:\:\:\:\mathrm{or}\:\:\:\:\mathrm{x}\:=\:−\:\mathrm{1} \\ $$$$ \\ $$

Commented by Tawa1 last updated on 23/Jul/19

Hahahaha, i solve like sir MrW, sir Mjs , sir Tanmay, sir Ajfour, Am learning everyday here. God bless everybody here.

$$\mathrm{Hahahaha},\:\:\mathrm{i}\:\mathrm{solve}\:\mathrm{like}\:\mathrm{sir}\:\:\mathrm{MrW},\:\:\mathrm{sir}\:\:\mathrm{Mjs}\:,\:\:\:\mathrm{sir}\:\:\mathrm{Tanmay},\:\:\mathrm{sir}\:\mathrm{Ajfour}, \\ $$$$\mathrm{Am}\:\mathrm{learning}\:\mathrm{everyday}\:\mathrm{here}.\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{everybody}\:\mathrm{here}.\: \\ $$

Commented by MJS last updated on 23/Jul/19

$$\mathrm{good}! \\ $$

Commented by mathmax by abdo last updated on 23/Jul/19

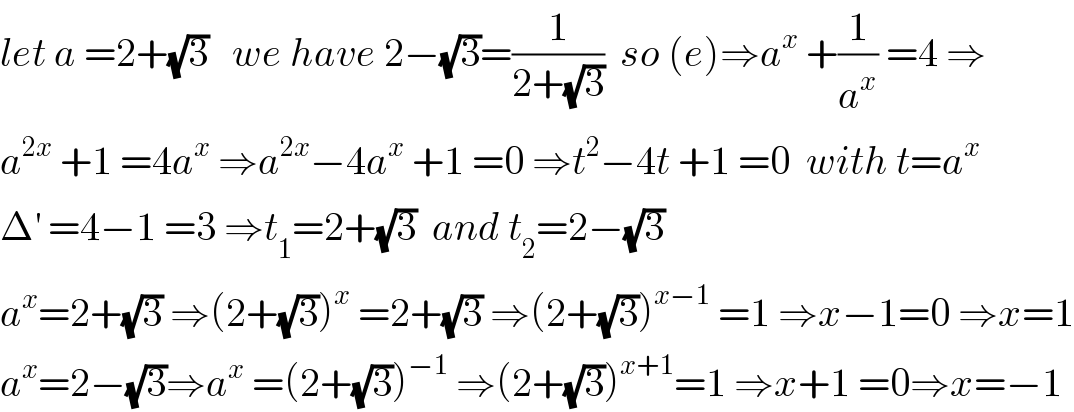
let a =2+(√3) we have 2−(√3)=(1/(2+(√3))) so (e)⇒a^x +(1/a^x ) =4 ⇒ a^(2x) +1 =4a^x ⇒a^(2x) −4a^x +1 =0 ⇒t^2 −4t +1 =0 with t=a^x Δ^′ =4−1 =3 ⇒t_1 =2+(√3) and t_2 =2−(√3) a^x =2+(√3) ⇒(2+(√3))^x =2+(√3) ⇒(2+(√3))^(x−1) =1 ⇒x−1=0 ⇒x=1 a^x =2−(√3)⇒a^x =(2+(√3))^(−1) ⇒(2+(√3))^(x+1) =1 ⇒x+1 =0⇒x=−1

$${let}\:{a}\:=\mathrm{2}+\sqrt{\mathrm{3}}\:\:\:{we}\:{have}\:\mathrm{2}−\sqrt{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{3}}}\:\:{so}\:\left({e}\right)\Rightarrow{a}^{{x}} \:+\frac{\mathrm{1}}{{a}^{{x}} }\:=\mathrm{4}\:\Rightarrow \\ $$$${a}^{\mathrm{2}{x}} \:+\mathrm{1}\:=\mathrm{4}{a}^{{x}} \:\Rightarrow{a}^{\mathrm{2}{x}} −\mathrm{4}{a}^{{x}} \:+\mathrm{1}\:=\mathrm{0}\:\Rightarrow{t}^{\mathrm{2}} −\mathrm{4}{t}\:+\mathrm{1}\:=\mathrm{0}\:\:{with}\:{t}={a}^{{x}} \\ $$$$\Delta^{'} \:=\mathrm{4}−\mathrm{1}\:=\mathrm{3}\:\Rightarrow{t}_{\mathrm{1}} =\mathrm{2}+\sqrt{\mathrm{3}}\:\:{and}\:{t}_{\mathrm{2}} =\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$${a}^{{x}} =\mathrm{2}+\sqrt{\mathrm{3}}\:\Rightarrow\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{{x}} \:=\mathrm{2}+\sqrt{\mathrm{3}}\:\Rightarrow\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{{x}−\mathrm{1}} \:=\mathrm{1}\:\Rightarrow{x}−\mathrm{1}=\mathrm{0}\:\Rightarrow{x}=\mathrm{1} \\ $$$${a}^{{x}} =\mathrm{2}−\sqrt{\mathrm{3}}\Rightarrow{a}^{{x}} \:=\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{−\mathrm{1}} \:\Rightarrow\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{{x}+\mathrm{1}} =\mathrm{1}\:\Rightarrow{x}+\mathrm{1}\:=\mathrm{0}\Rightarrow{x}=−\mathrm{1} \\ $$

Commented by Masumsiddiqui399@gmail.com last updated on 23/Jul/19

$${thank}\:{u}\:{sir} \\ $$

Commented by Masumsiddiqui399@gmail.com last updated on 23/Jul/19

$${thank}\:{u}\:{sir} \\ $$

Answered by MJS last updated on 23/Jul/19

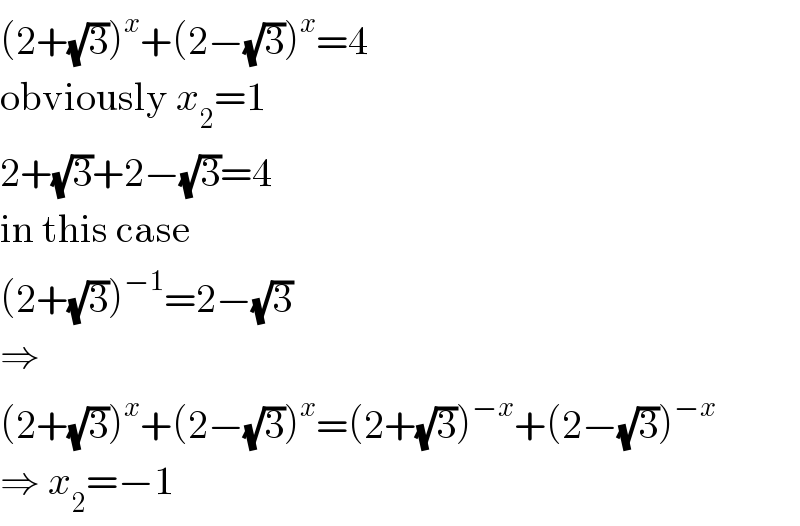
(2+(√3))^x +(2−(√3))^x =4 obviously x_2 =1 2+(√3)+2−(√3)=4 in this case (2+(√3))^(−1) =2−(√3) ⇒ (2+(√3))^x +(2−(√3))^x =(2+(√3))^(−x) +(2−(√3))^(−x) ⇒ x_2 =−1

$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{{x}} +\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{{x}} =\mathrm{4} \\ $$$$\mathrm{obviously}\:{x}_{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{2}+\sqrt{\mathrm{3}}+\mathrm{2}−\sqrt{\mathrm{3}}=\mathrm{4} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{−\mathrm{1}} =\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\Rightarrow \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{{x}} +\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{{x}} =\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{−{x}} +\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{−{x}} \\ $$$$\Rightarrow\:{x}_{\mathrm{2}} =−\mathrm{1} \\ $$

Commented by MJS last updated on 23/Jul/19

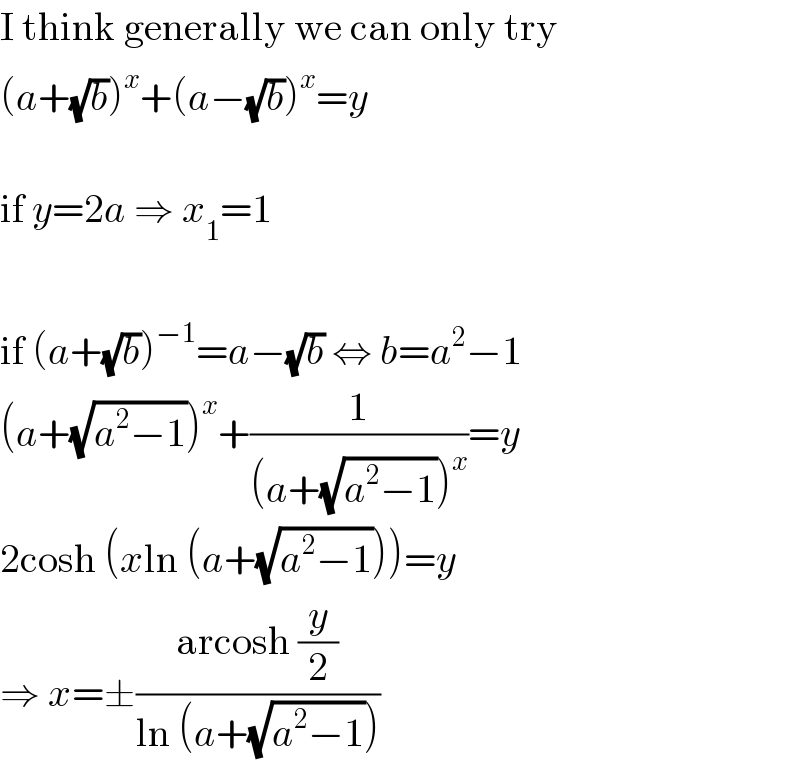
I think generally we can only try (a+(√b))^x +(a−(√b))^x =y if y=2a ⇒ x_1 =1 if (a+(√b))^(−1) =a−(√b) ⇔ b=a^2 −1 (a+(√(a^2 −1)))^x +(1/((a+(√(a^2 −1)))^x ))=y 2cosh (xln (a+(√(a^2 −1))))=y ⇒ x=±((arcosh (y/2))/(ln (a+(√(a^2 −1)))))

$$\mathrm{I}\:\mathrm{think}\:\mathrm{generally}\:\mathrm{we}\:\mathrm{can}\:\mathrm{only}\:\mathrm{try} \\ $$$$\left({a}+\sqrt{{b}}\right)^{{x}} +\left({a}−\sqrt{{b}}\right)^{{x}} ={y} \\ $$$$ \\ $$$$\mathrm{if}\:{y}=\mathrm{2}{a}\:\Rightarrow\:{x}_{\mathrm{1}} =\mathrm{1} \\ $$$$ \\ $$$$\mathrm{if}\:\left({a}+\sqrt{{b}}\right)^{−\mathrm{1}} ={a}−\sqrt{{b}}\:\Leftrightarrow\:{b}={a}^{\mathrm{2}} −\mathrm{1} \\ $$$$\left({a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}\right)^{{x}} +\frac{\mathrm{1}}{\left({a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}\right)^{{x}} }={y} \\ $$$$\mathrm{2cosh}\:\left({x}\mathrm{ln}\:\left({a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}\right)\right)={y} \\ $$$$\Rightarrow\:{x}=\pm\frac{\mathrm{arcosh}\:\frac{{y}}{\mathrm{2}}}{\mathrm{ln}\:\left({a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}\right)} \\ $$

Commented by Tawa1 last updated on 23/Jul/19

Wow, God bless you sir. I will note this too.

$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{I}\:\mathrm{will}\:\mathrm{note}\:\mathrm{this}\:\mathrm{too}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply