Question-64951

Question Number 64951 by naka3546 last updated on 23/Jul/19

Answered by mr W last updated on 23/Jul/19

Commented by mr W last updated on 23/Jul/19

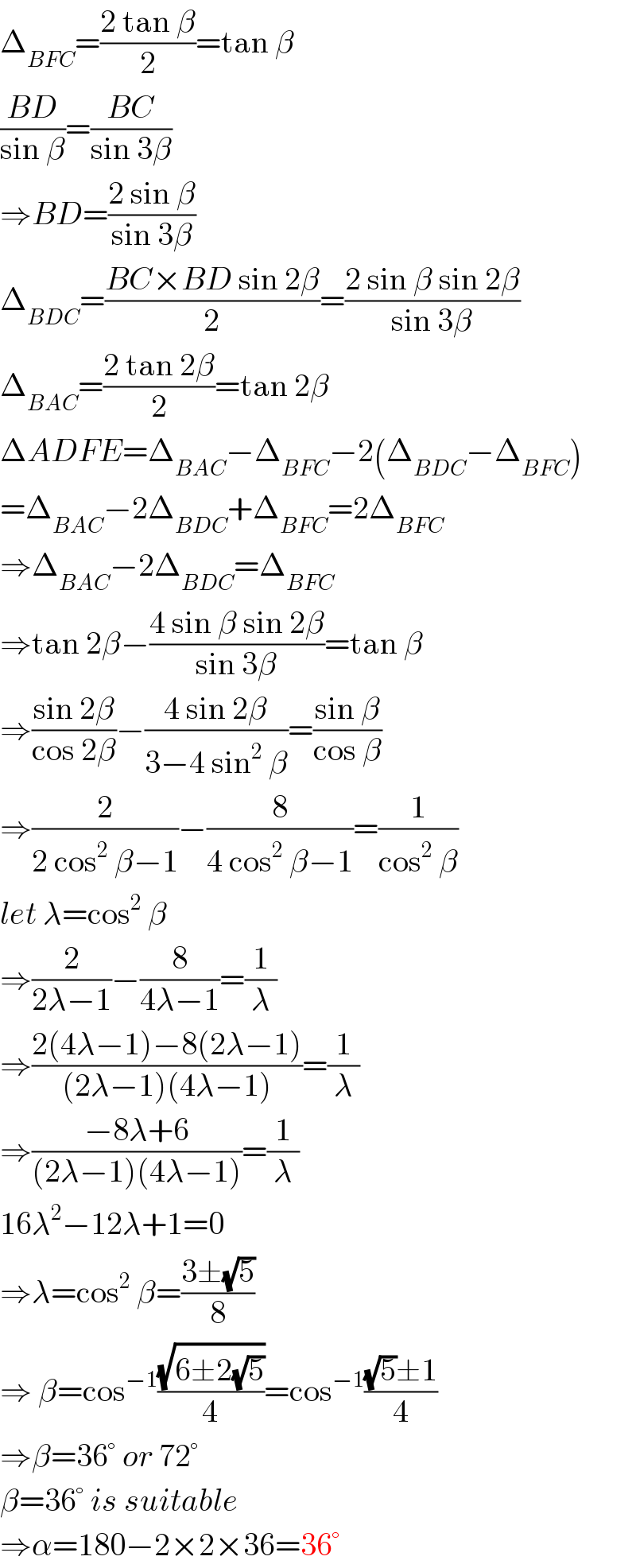
Δ_(BFC) =((2 tan β)/2)=tan β ((BD)/(sin β))=((BC)/(sin 3β)) ⇒BD=((2 sin β)/(sin 3β)) Δ_(BDC) =((BC×BD sin 2β)/2)=((2 sin β sin 2β)/(sin 3β)) Δ_(BAC) =((2 tan 2β)/2)=tan 2β ΔADFE=Δ_(BAC) −Δ_(BFC) −2(Δ_(BDC) −Δ_(BFC) ) =Δ_(BAC) −2Δ_(BDC) +Δ_(BFC) =2Δ_(BFC) ⇒Δ_(BAC) −2Δ_(BDC) =Δ_(BFC) ⇒tan 2β−((4 sin β sin 2β)/(sin 3β))=tan β ⇒((sin 2β)/(cos 2β))−((4 sin 2β)/(3−4 sin^2 β))=((sin β)/(cos β)) ⇒(2/(2 cos^2 β−1))−(8/(4 cos^2 β−1))=(1/(cos^2 β)) let λ=cos^2 β ⇒(2/(2λ−1))−(8/(4λ−1))=(1/λ) ⇒((2(4λ−1)−8(2λ−1))/((2λ−1)(4λ−1)))=(1/λ) ⇒((−8λ+6)/((2λ−1)(4λ−1)))=(1/λ) 16λ^2 −12λ+1=0 ⇒λ=cos^2 β=((3±(√5))/8) ⇒ β=cos^(−1) ((√(6±2(√5)))/4)=cos^(−1) (((√5)±1)/4) ⇒β=36° or 72° β=36° is suitable ⇒α=180−2×2×36=36°

$$\Delta_{{BFC}} =\frac{\mathrm{2}\:\mathrm{tan}\:\beta}{\mathrm{2}}=\mathrm{tan}\:\beta \\ $$$$\frac{{BD}}{\mathrm{sin}\:\beta}=\frac{{BC}}{\mathrm{sin}\:\mathrm{3}\beta} \\ $$$$\Rightarrow{BD}=\frac{\mathrm{2}\:\mathrm{sin}\:\beta}{\mathrm{sin}\:\mathrm{3}\beta} \\ $$$$\Delta_{{BDC}} =\frac{{BC}×{BD}\:\mathrm{sin}\:\mathrm{2}\beta}{\mathrm{2}}=\frac{\mathrm{2}\:\mathrm{sin}\:\beta\:\mathrm{sin}\:\mathrm{2}\beta}{\mathrm{sin}\:\mathrm{3}\beta} \\ $$$$\Delta_{{BAC}} =\frac{\mathrm{2}\:\mathrm{tan}\:\mathrm{2}\beta}{\mathrm{2}}=\mathrm{tan}\:\mathrm{2}\beta \\ $$$$\Delta{ADFE}=\Delta_{{BAC}} −\Delta_{{BFC}} −\mathrm{2}\left(\Delta_{{BDC}} −\Delta_{{BFC}} \right) \\ $$$$=\Delta_{{BAC}} −\mathrm{2}\Delta_{{BDC}} +\Delta_{{BFC}} =\mathrm{2}\Delta_{{BFC}} \\ $$$$\Rightarrow\Delta_{{BAC}} −\mathrm{2}\Delta_{{BDC}} =\Delta_{{BFC}} \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{2}\beta−\frac{\mathrm{4}\:\mathrm{sin}\:\beta\:\mathrm{sin}\:\mathrm{2}\beta}{\mathrm{sin}\:\mathrm{3}\beta}=\mathrm{tan}\:\beta \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\mathrm{2}\beta}{\mathrm{cos}\:\mathrm{2}\beta}−\frac{\mathrm{4}\:\mathrm{sin}\:\mathrm{2}\beta}{\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\beta}=\frac{\mathrm{sin}\:\beta}{\mathrm{cos}\:\beta} \\ $$$$\Rightarrow\frac{\mathrm{2}}{\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\beta−\mathrm{1}}−\frac{\mathrm{8}}{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\beta−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\beta} \\ $$$${let}\:\lambda=\mathrm{cos}^{\mathrm{2}} \:\beta \\ $$$$\Rightarrow\frac{\mathrm{2}}{\mathrm{2}\lambda−\mathrm{1}}−\frac{\mathrm{8}}{\mathrm{4}\lambda−\mathrm{1}}=\frac{\mathrm{1}}{\lambda} \\ $$$$\Rightarrow\frac{\mathrm{2}\left(\mathrm{4}\lambda−\mathrm{1}\right)−\mathrm{8}\left(\mathrm{2}\lambda−\mathrm{1}\right)}{\left(\mathrm{2}\lambda−\mathrm{1}\right)\left(\mathrm{4}\lambda−\mathrm{1}\right)}=\frac{\mathrm{1}}{\lambda} \\ $$$$\Rightarrow\frac{−\mathrm{8}\lambda+\mathrm{6}}{\left(\mathrm{2}\lambda−\mathrm{1}\right)\left(\mathrm{4}\lambda−\mathrm{1}\right)}=\frac{\mathrm{1}}{\lambda} \\ $$$$\mathrm{16}\lambda^{\mathrm{2}} −\mathrm{12}\lambda+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\lambda=\mathrm{cos}^{\mathrm{2}} \:\beta=\frac{\mathrm{3}\pm\sqrt{\mathrm{5}}}{\mathrm{8}} \\ $$$$\Rightarrow\:\beta=\mathrm{cos}^{−\mathrm{1}} \frac{\sqrt{\mathrm{6}\pm\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}=\mathrm{cos}^{−\mathrm{1}} \frac{\sqrt{\mathrm{5}}\pm\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\beta=\mathrm{36}°\:{or}\:\mathrm{72}° \\ $$$$\beta=\mathrm{36}°\:{is}\:{suitable} \\ $$$$\Rightarrow\alpha=\mathrm{180}−\mathrm{2}×\mathrm{2}×\mathrm{36}=\mathrm{36}° \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply