Question Number 64973 by Tawa1 last updated on 23/Jul/19
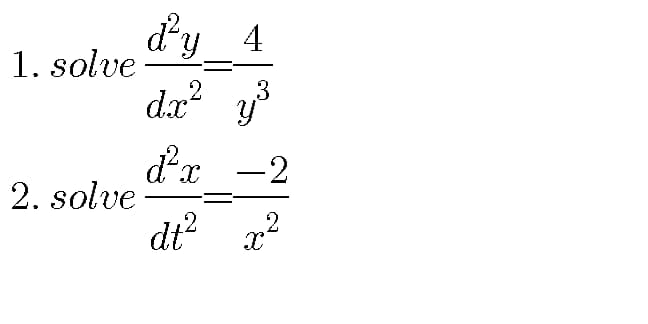
Answered by mr W last updated on 23/Jul/19
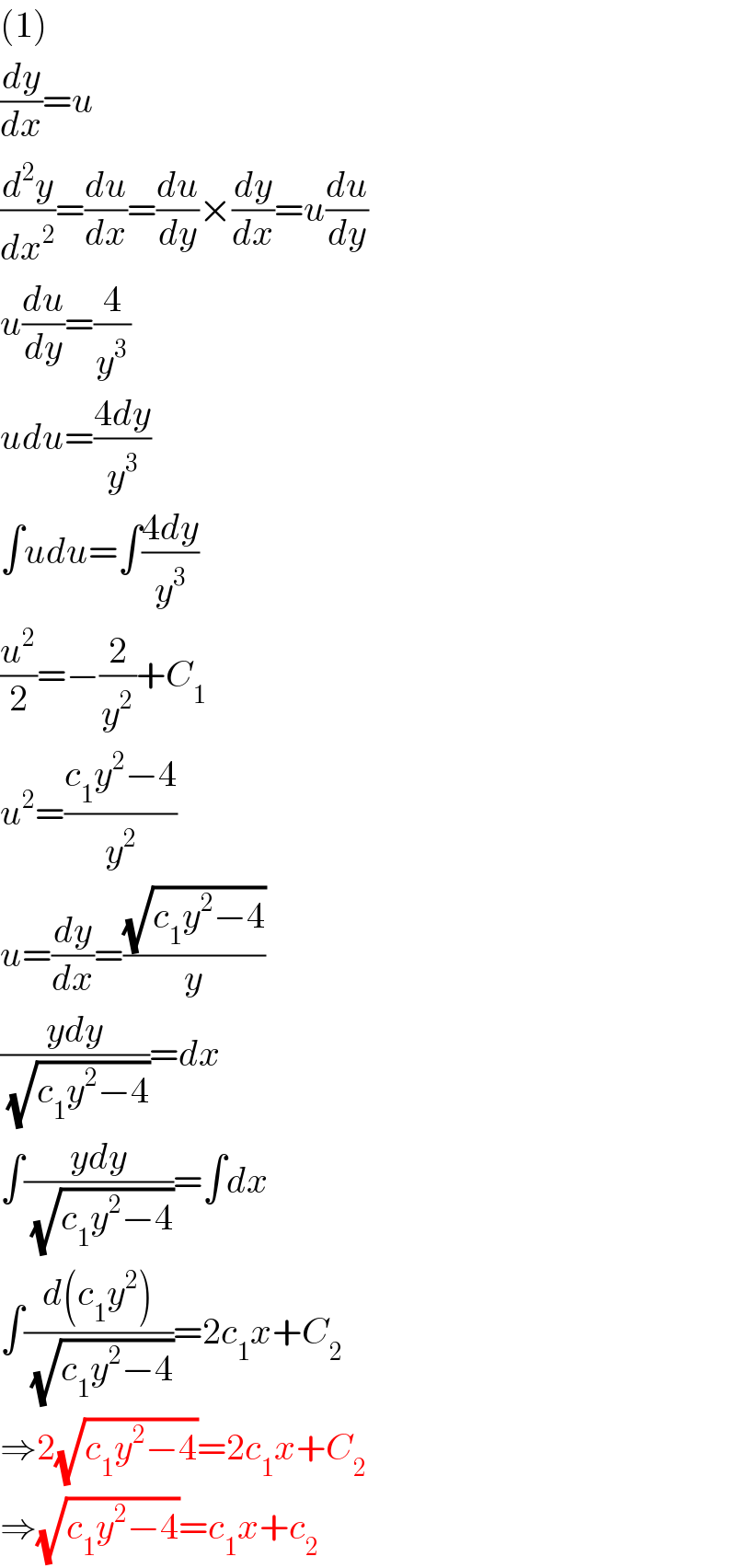
$$\left(\mathrm{1}\right) \\ $$$$\frac{{dy}}{{dx}}={u} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{du}}{{dx}}=\frac{{du}}{{dy}}×\frac{{dy}}{{dx}}={u}\frac{{du}}{{dy}} \\ $$$${u}\frac{{du}}{{dy}}=\frac{\mathrm{4}}{{y}^{\mathrm{3}} } \\ $$$${udu}=\frac{\mathrm{4}{dy}}{{y}^{\mathrm{3}} } \\ $$$$\int{udu}=\int\frac{\mathrm{4}{dy}}{{y}^{\mathrm{3}} } \\ $$$$\frac{{u}^{\mathrm{2}} }{\mathrm{2}}=−\frac{\mathrm{2}}{{y}^{\mathrm{2}} }+{C}_{\mathrm{1}} \\ $$$${u}^{\mathrm{2}} =\frac{{c}_{\mathrm{1}} {y}^{\mathrm{2}} −\mathrm{4}}{{y}^{\mathrm{2}} } \\ $$$${u}=\frac{{dy}}{{dx}}=\frac{\sqrt{{c}_{\mathrm{1}} {y}^{\mathrm{2}} −\mathrm{4}}}{{y}} \\ $$$$\frac{{ydy}}{\:\sqrt{{c}_{\mathrm{1}} {y}^{\mathrm{2}} −\mathrm{4}}}={dx} \\ $$$$\int\frac{{ydy}}{\:\sqrt{{c}_{\mathrm{1}} {y}^{\mathrm{2}} −\mathrm{4}}}=\int{dx} \\ $$$$\int\frac{{d}\left({c}_{\mathrm{1}} {y}^{\mathrm{2}} \right)}{\:\sqrt{{c}_{\mathrm{1}} {y}^{\mathrm{2}} −\mathrm{4}}}=\mathrm{2}{c}_{\mathrm{1}} {x}+{C}_{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}\sqrt{{c}_{\mathrm{1}} {y}^{\mathrm{2}} −\mathrm{4}}=\mathrm{2}{c}_{\mathrm{1}} {x}+{C}_{\mathrm{2}} \\ $$$$\Rightarrow\sqrt{{c}_{\mathrm{1}} {y}^{\mathrm{2}} −\mathrm{4}}={c}_{\mathrm{1}} {x}+{c}_{\mathrm{2}} \\ $$
Commented by Tawa1 last updated on 23/Jul/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
