Question Number 65077 by naka3546 last updated on 24/Jul/19
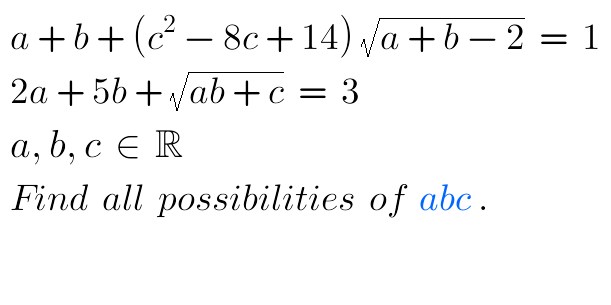
Answered by MJS last updated on 25/Jul/19
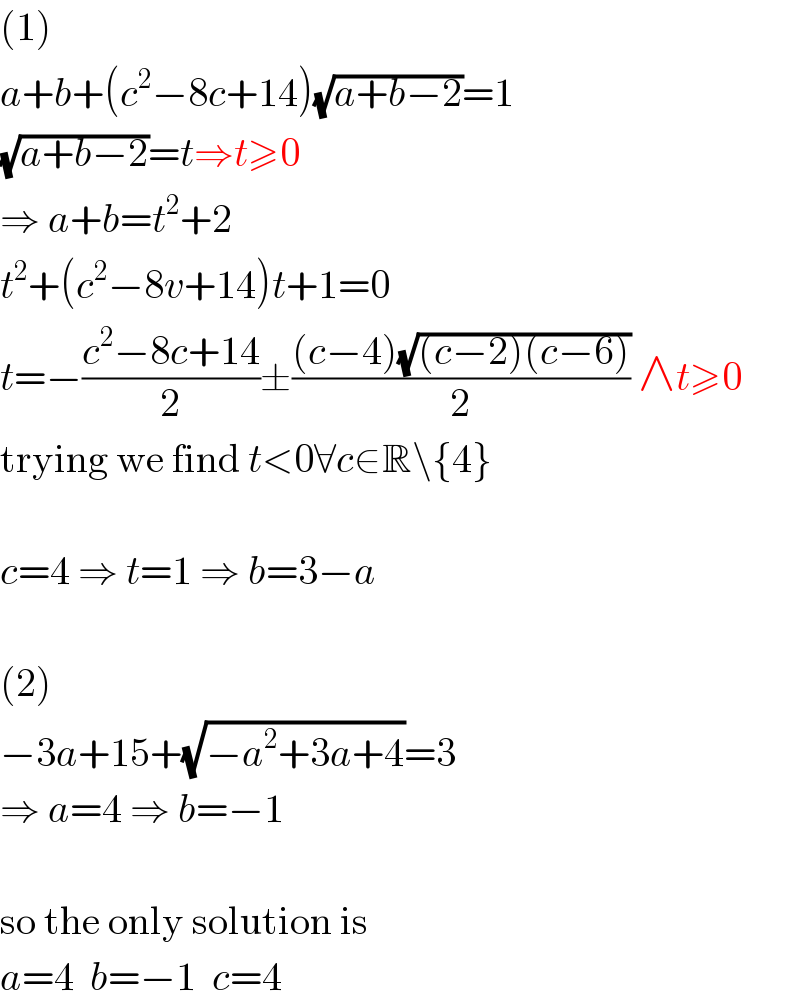
$$\left(\mathrm{1}\right) \\ $$$${a}+{b}+\left({c}^{\mathrm{2}} −\mathrm{8}{c}+\mathrm{14}\right)\sqrt{{a}+{b}−\mathrm{2}}=\mathrm{1} \\ $$$$\sqrt{{a}+{b}−\mathrm{2}}={t}\Rightarrow{t}\geqslant\mathrm{0} \\ $$$$\Rightarrow\:{a}+{b}={t}^{\mathrm{2}} +\mathrm{2} \\ $$$${t}^{\mathrm{2}} +\left({c}^{\mathrm{2}} −\mathrm{8}{v}+\mathrm{14}\right){t}+\mathrm{1}=\mathrm{0} \\ $$$${t}=−\frac{{c}^{\mathrm{2}} −\mathrm{8}{c}+\mathrm{14}}{\mathrm{2}}\pm\frac{\left({c}−\mathrm{4}\right)\sqrt{\left({c}−\mathrm{2}\right)\left({c}−\mathrm{6}\right)}}{\mathrm{2}}\:\wedge{t}\geqslant\mathrm{0} \\ $$$$\mathrm{trying}\:\mathrm{we}\:\mathrm{find}\:{t}<\mathrm{0}\forall{c}\in\mathbb{R}\backslash\left\{\mathrm{4}\right\} \\ $$$$ \\ $$$${c}=\mathrm{4}\:\Rightarrow\:{t}=\mathrm{1}\:\Rightarrow\:{b}=\mathrm{3}−{a} \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$$−\mathrm{3}{a}+\mathrm{15}+\sqrt{−{a}^{\mathrm{2}} +\mathrm{3}{a}+\mathrm{4}}=\mathrm{3} \\ $$$$\Rightarrow\:{a}=\mathrm{4}\:\Rightarrow\:{b}=−\mathrm{1} \\ $$$$ \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{only}\:\mathrm{solution}\:\mathrm{is} \\ $$$${a}=\mathrm{4}\:\:{b}=−\mathrm{1}\:\:{c}=\mathrm{4} \\ $$
