Question Number 65200 by rajesh4661kumar@gmail.com last updated on 26/Jul/19
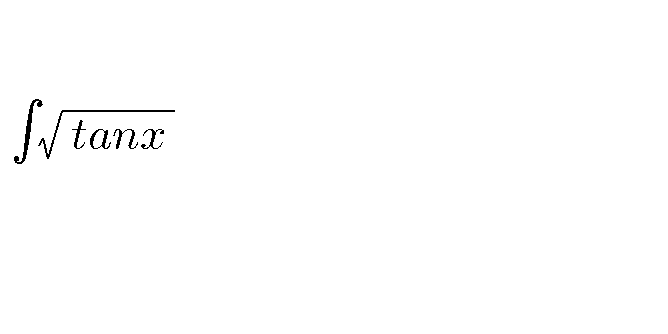
Answered by ajfour last updated on 26/Jul/19
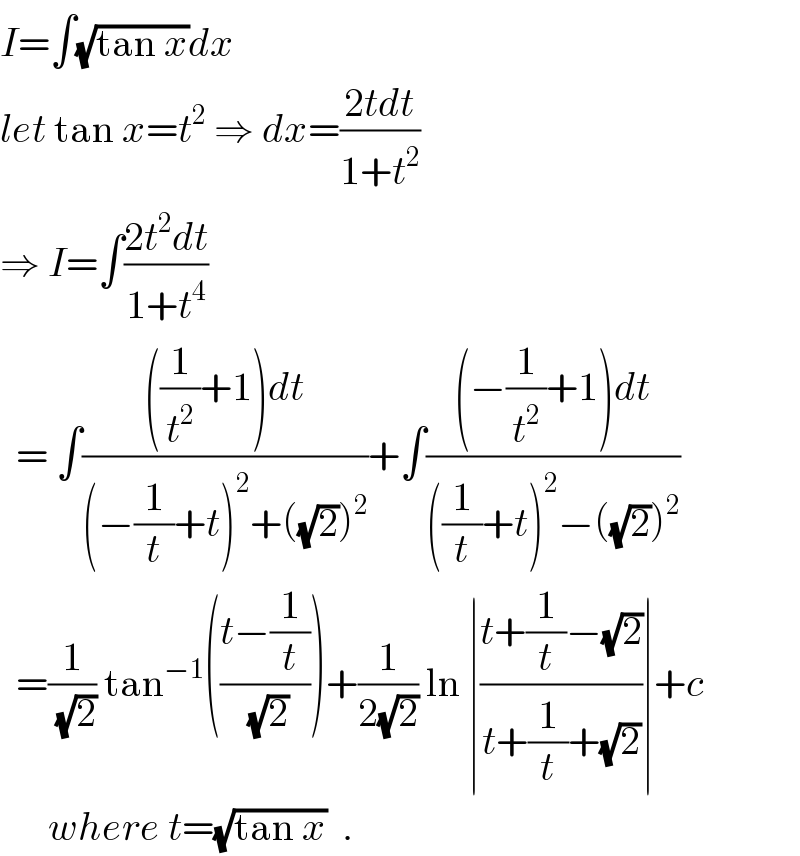
$${I}=\int\sqrt{\mathrm{tan}\:{x}}{dx} \\ $$$${let}\:\mathrm{tan}\:{x}={t}^{\mathrm{2}} \:\Rightarrow\:{dx}=\frac{\mathrm{2}{tdt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{I}=\int\frac{\mathrm{2}{t}^{\mathrm{2}} {dt}}{\mathrm{1}+{t}^{\mathrm{4}} } \\ $$$$\:\:=\:\int\frac{\left(\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\mathrm{1}\right){dt}}{\left(−\frac{\mathrm{1}}{{t}}+{t}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }+\int\frac{\left(−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\mathrm{1}\right){dt}}{\left(\frac{\mathrm{1}}{{t}}+{t}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{t}−\frac{\mathrm{1}}{{t}}}{\:\sqrt{\mathrm{2}}}\right)+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\mathrm{ln}\:\mid\frac{{t}+\frac{\mathrm{1}}{{t}}−\sqrt{\mathrm{2}}}{{t}+\frac{\mathrm{1}}{{t}}+\sqrt{\mathrm{2}}}\mid+{c} \\ $$$$\:\:\:\:\:\:{where}\:{t}=\sqrt{\mathrm{tan}\:{x}}\:\:. \\ $$
Answered by zakaria elghaouti last updated on 27/Jul/19

