Question Number 65212 by ajfour last updated on 26/Jul/19
Commented by ajfour last updated on 26/Jul/19
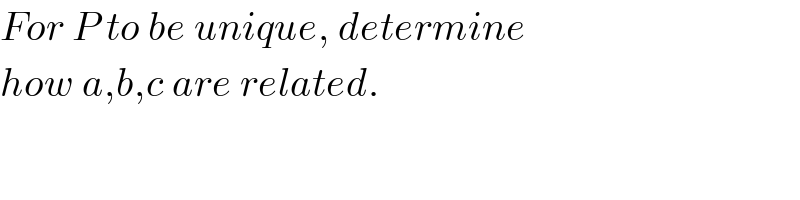
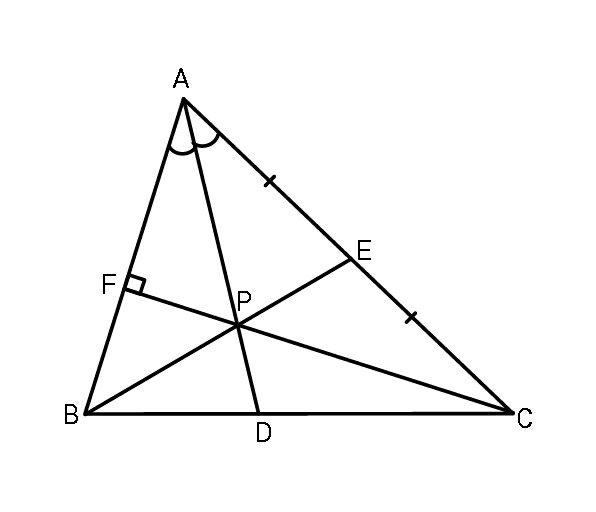
$${For}\:{P}\:{to}\:{be}\:{unique},\:{determine} \\ $$$${how}\:{a},{b},{c}\:{are}\:{related}. \\ $$
Answered by ajfour last updated on 26/Jul/19

$${let}\:{B}\left(\mathrm{0},\mathrm{0}\right) \\ $$$${C}\left({a},\mathrm{0}\right)\:\:\:,\:\:{D}\left(\frac{{ac}}{{b}+{c}},\mathrm{0}\right) \\ $$$$\underset{−} {{For}\:{A}\left({h},{k}\right)} \\ $$$$\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={c}^{\mathrm{2}} \\ $$$$\:\:\left({x}−{a}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$$\Rightarrow\:{a}\left(\mathrm{2}{x}−{a}\right)={c}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{x}_{{A}} ={h}=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{a}} \\ $$$$\:\:{y}_{{A}} ={k}=\sqrt{{c}^{\mathrm{2}} −\left(\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{a}}\right)^{\mathrm{2}} } \\ $$$$\underset{−} {{eq}.\:{of}\:{BE}}\:\:\:\:\:\:\:{y}=\frac{{kx}}{{a}+{h}} \\ $$$$\underset{−} {{eq}.\:{of}\:{CF}}\:\:\:\:\:\:\:{y}=−\frac{{h}}{{k}}\left({x}−{a}\right) \\ $$$$\underset{−} {{eq}.\:{of}\:{AD}}\:\:\:\:\:\:{y}=\frac{{k}\left({x}−\frac{{ac}}{{b}+{c}}\right)}{\left({h}−\frac{{ac}}{{b}+{c}}\right)} \\ $$$${For}\:{intersection}\:{of}\:{BE},\:{CF} \\ $$$$\:\:\frac{{kx}}{{a}+{h}}=−\frac{{h}}{{k}}\left({x}−{a}\right) \\ $$$$\Rightarrow\:\:{k}^{\mathrm{2}} {x}+{h}\left({a}+{h}\right){x}={ah}\left({a}+{h}\right) \\ $$$$\Rightarrow\:\:{x}_{{P}} =\frac{{ah}\left({a}+{h}\right)}{{k}^{\mathrm{2}} +{h}\left({a}+{h}\right)} \\ $$$$\:\:\:\:\:\:\:{y}_{{P}} =\frac{{ahk}}{{k}^{\mathrm{2}} +{h}\left({a}+{h}\right)} \\ $$$${If}\:{P}\:{is}\:{unique},\:\:{P}\:{even}\:{lies}\:{on}\:{AD} \\ $$$$\Rightarrow\:\:\frac{{ahk}}{{k}^{\mathrm{2}} +{h}\left({a}+{h}\right)}=\frac{{k}\left(\frac{{ah}\left({a}+{h}\right)}{{k}^{\mathrm{2}} +{h}\left({a}+{h}\right)}−\frac{{ac}}{{b}+{c}}\right)}{\left({h}−\frac{{ac}}{{b}+{c}}\right)} \\ $$$${where}\:\:{h}=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{a}} \\ $$$${and}\:\:\:\:\:\:\:{k}=\sqrt{{c}^{\mathrm{2}} −\left(\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{a}}\right)^{\mathrm{2}} } \\ $$$${with}\:{little}\:{rearrangements} \\ $$$${after}\:{substitution}\:{and}\:{if} \\ $$$${k}\neq\mathrm{0},\:{a}\neq\mathrm{0}\:,\:{i}\:{arrived}\:{at} \\ $$$$\:\:\:{ah}\left({b}+{c}\right)={c}\left({h}^{\mathrm{2}} +{k}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:{a}\left({b}+{c}\right)\left(\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{a}}\right)={c}^{\mathrm{3}} \\ $$$$\Rightarrow\:\left({b}+{c}\right)\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\:=\:\mathrm{2}{c}^{\mathrm{3}} \\ $$$$\Rightarrow\:\:\left({b}+{c}\right)\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\:=\:{c}^{\mathrm{2}} \left({c}−{b}\right) \\ $$$$\Rightarrow\:\:\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{c}^{\mathrm{2}} }=\frac{{c}−{b}}{{c}+{b}}\:\:. \\ $$
Commented by mr W last updated on 26/Jul/19

$${nice}\:{solution}! \\ $$
