Menu Close

Question-65227

Tinku Tara 0 Comments
Pin




Question Number 65227 by Tawa1 last updated on 26/Jul/19
Commented by Tony Lin last updated on 26/Jul/19
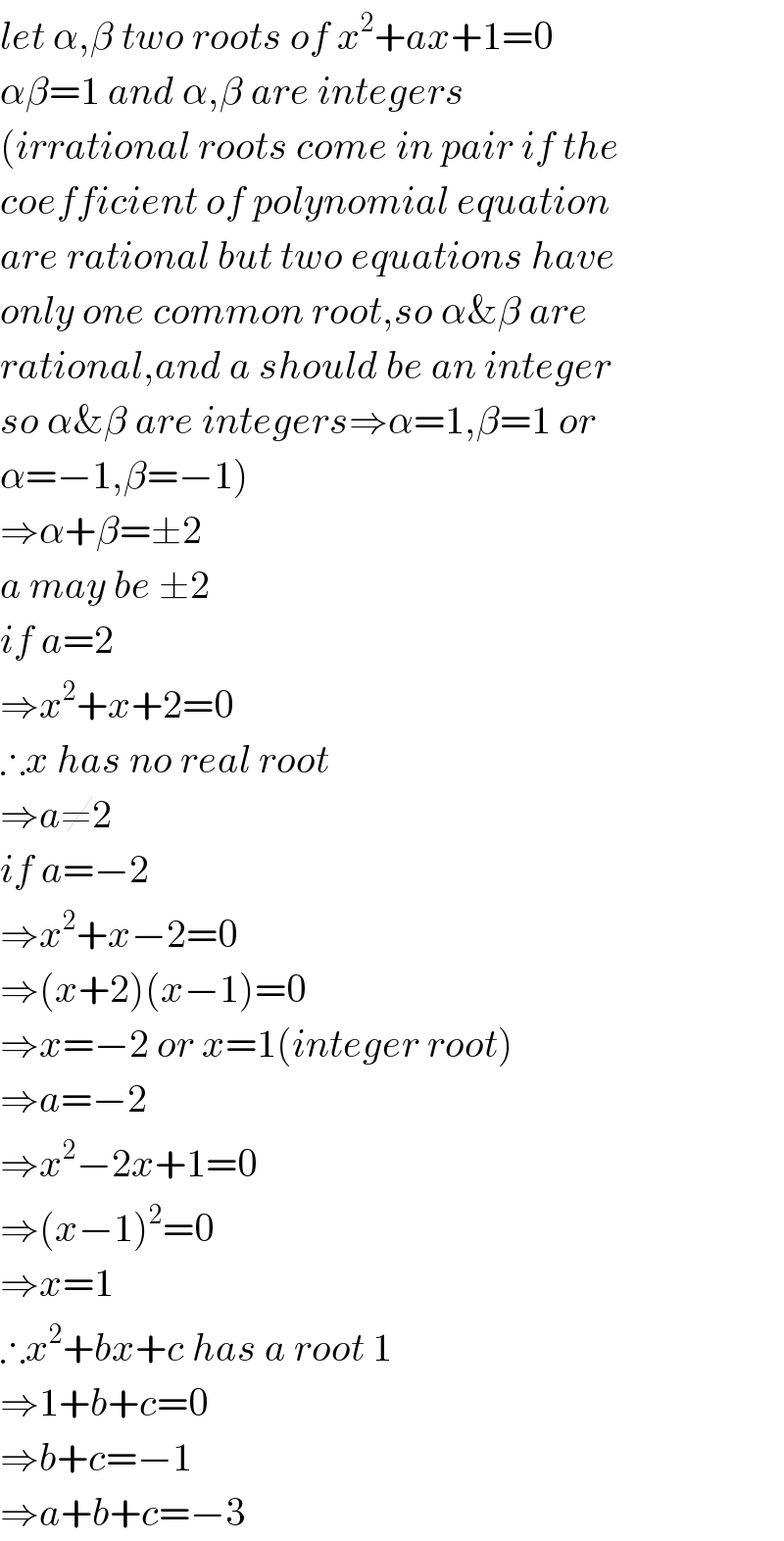
let α,β two roots of x^2 +ax+1=0 αβ=1 and α,β are integers (irrational roots come in pair if the coefficient of polynomial equation are rational but two equations have only one common root,so α&β are rational,and a should be an integer so α&β are integers⇒α=1,β=1 or α=−1,β=−1) ⇒α+β=±2 a may be ±2 if a=2 ⇒x^2 +x+2=0 ∴x has no real root ⇒a≠2 if a=−2 ⇒x^2 +x−2=0 ⇒(x+2)(x−1)=0 ⇒x=−2 or x=1(integer root) ⇒a=−2 ⇒x^2 −2x+1=0 ⇒(x−1)^2 =0 ⇒x=1 ∴x^2 +bx+c has a root 1 ⇒1+b+c=0 ⇒b+c=−1 ⇒a+b+c=−3
$${let}\:\alpha,\beta\:{two}\:{roots}\:{of}\:{x}^{\mathrm{2}} +{ax}+\mathrm{1}=\mathrm{0} \\ $$$$\alpha\beta=\mathrm{1}\:{and}\:\alpha,\beta\:{are}\:{integers} \\ $$$$\left({irrational}\:{roots}\:{come}\:{in}\:{pair}\:{if}\:{the}\right. \\ $$$${coefficient}\:{of}\:{polynomial}\:{equation} \\ $$$${are}\:{rational}\:{but}\:{two}\:{equations}\:{have}\: \\ $$$${only}\:{one}\:{common}\:{root},{so}\:\alpha\&\beta\:{are} \\ $$$${rational},{and}\:{a}\:{should}\:{be}\:{an}\:{integer} \\ $$$${so}\:\alpha\&\beta\:{are}\:{integers}\Rightarrow\alpha=\mathrm{1},\beta=\mathrm{1}\:{or} \\ $$$$\left.\alpha=−\mathrm{1},\beta=−\mathrm{1}\right) \\ $$$$\Rightarrow\alpha+\beta=\pm\mathrm{2} \\ $$$${a}\:{may}\:{be}\:\pm\mathrm{2} \\ $$$${if}\:{a}=\mathrm{2} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{x}+\mathrm{2}=\mathrm{0} \\ $$$$\therefore{x}\:{has}\:{no}\:{real}\:{root} \\ $$$$\Rightarrow{a}\neq\mathrm{2} \\ $$$${if}\:{a}=−\mathrm{2} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{x}−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\left({x}+\mathrm{2}\right)\left({x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=−\mathrm{2}\:{or}\:{x}=\mathrm{1}\left({integer}\:{root}\right) \\ $$$$\Rightarrow{a}=−\mathrm{2} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left({x}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{1} \\ $$$$\therefore{x}^{\mathrm{2}} +{bx}+{c}\:{has}\:{a}\:{root}\:\mathrm{1} \\ $$$$\Rightarrow\mathrm{1}+{b}+{c}=\mathrm{0} \\ $$$$\Rightarrow{b}+{c}=−\mathrm{1} \\ $$$$\Rightarrow{a}+{b}+{c}=−\mathrm{3} \\ $$
Commented by Tawa1 last updated on 26/Jul/19
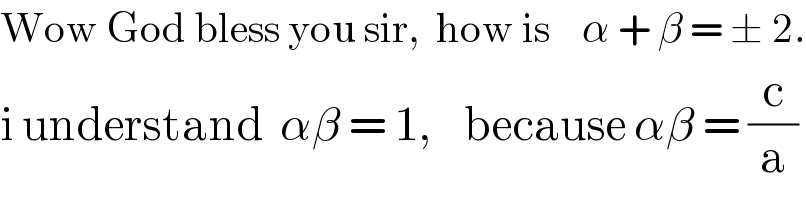
Wow God bless you sir, how is α + β = ± 2. i understand αβ = 1, because αβ = (c/a)
$$\mathrm{Wow}\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\:\mathrm{how}\:\mathrm{is}\:\:\:\:\alpha\:+\:\beta\:=\:\pm\:\mathrm{2}. \\ $$$$\mathrm{i}\:\mathrm{understand}\:\:\alpha\beta\:=\:\mathrm{1},\:\:\:\:\mathrm{because}\:\alpha\beta\:=\:\frac{\mathrm{c}}{\mathrm{a}} \\ $$
Commented by Tawa1 last updated on 26/Jul/19
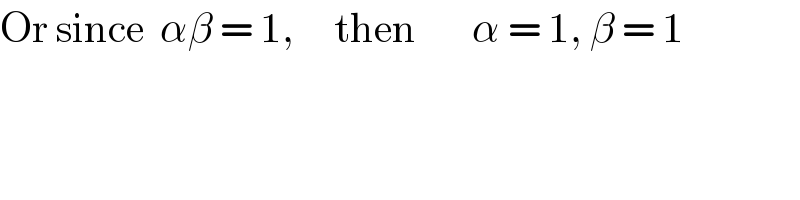
Or since αβ = 1, then α = 1, β = 1
$$\mathrm{Or}\:\mathrm{since}\:\:\alpha\beta\:=\:\mathrm{1},\:\:\:\:\:\mathrm{then}\:\:\:\:\:\:\:\alpha\:=\:\mathrm{1},\:\beta\:=\:\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *