Question Number 65281 by mr W last updated on 27/Jul/19

Commented by mr W last updated on 27/Jul/19
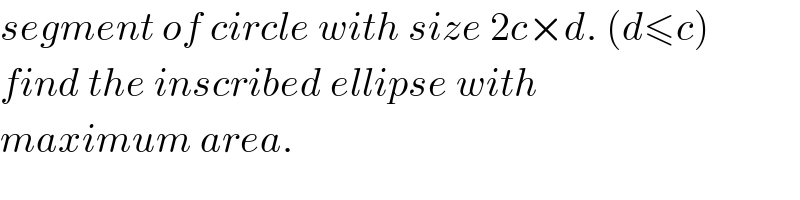
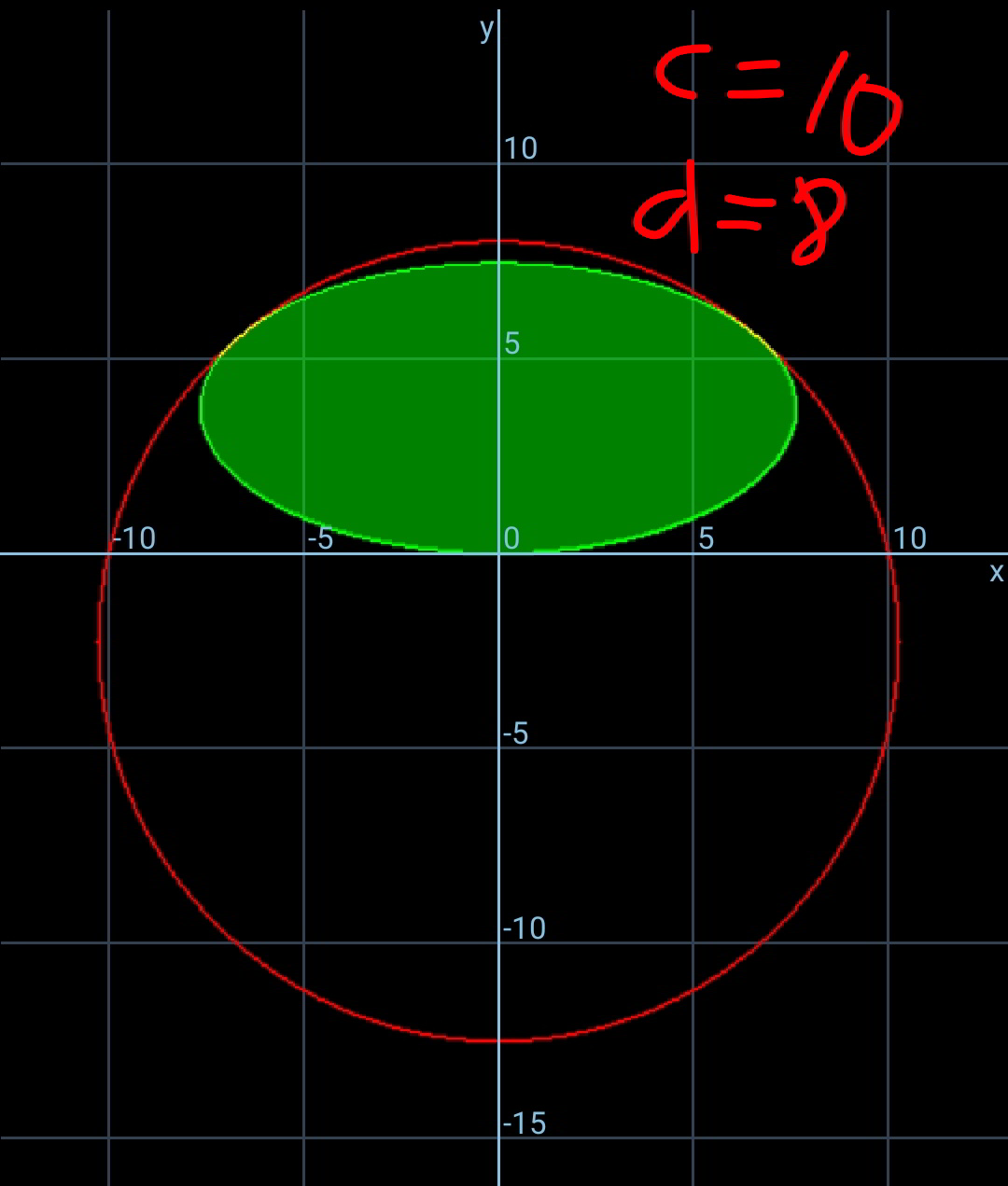
$${segment}\:{of}\:{circle}\:{with}\:{size}\:\mathrm{2}{c}×{d}.\:\left({d}\leqslant{c}\right) \\ $$$${find}\:{the}\:{inscribed}\:{ellipse}\:{with} \\ $$$${maximum}\:{area}. \\ $$
Answered by mr W last updated on 28/Jul/19
![R=radius of circle d(2R−d)=c^2 ⇒R=((c^2 +d^2 )/(2d)) let h=R−d=((c^2 −d^2 )/(2d)) eqn. of circle: x^2 +(y+h)^2 =R^2 x^2 +y^2 +2hy+h^2 −R^2 =0 ⇒x^2 +y^2 +2hy−c^2 =0 ...(i) eqn. of ellipse: (x^2 /a^2 )+(((y−b)^2 )/b^2 )=1 x^2 +(a^2 /b^2 )y^2 −((2a^2 )/b)y=0 ...(ii) (i)−(ii): (1−(a^2 /b^2 ))y^2 +2(h+(a^2 /b))y−c^2 =0 due to tangency there is only one root, Δ=4(h+(a^2 /b))^2 +4c^2 (1−(a^2 /b^2 ))=0 ⇒(hb+a^2 )^2 +c^2 (b^2 −a^2 )=0 ...(iii) ⇒(hab+a^3 )^2 +c^2 (a^2 b^2 −a^4 )=0 let P=ab ⇒(hP+a^3 )^2 +c^2 (P^2 −a^4 )=0 for maximum ellipse area, (dP/da)=0 ⇒2(hP+a^3 )(3a^2 )+c^2 (−4a^3 )=0 ⇒3(hb+a^2 )−2c^2 =0 if h=0, i.e. d=c: 3a^2 −2c^2 =0⇒a=(((√6)c)/3)⇒b=(((√2)c)/3) if h≠0: ⇒b=(1/h)(((2c^2 )/3)−a^2 ) insert this into (iii): (((2c^2 )/3)−a^2 +a^2 )^2 +c^2 (b^2 −a^2 )=0 ((4c^2 )/9)+(1/h^2 )(((2c^2 )/3)−a^2 )^2 −a^2 =0 ((4c^2 h^2 )/9)+(((2c^2 )/3)−a^2 )^2 −h^2 a^2 =0 a^4 −(((4c^2 )/3)+h^2 )a^2 +((4c^2 (c^2 +h^2 ))/9)=0 ⇒a^2 =(1/2)[((4c^2 )/3)+h^2 −(√((((4c^2 )/3)+h^2 )^2 −((16c^2 (c^2 +h^2 ))/9)))] ⇒a^2 =(1/2)[((4c^2 )/3)+h^2 −(√((16c^4 +24c^2 h^2 +9h^4 −16c^4 −16c^2 h^2 )/9))] ⇒a^2 =(1/2)(((4c^2 )/3)+h^2 −h(√(((8c^2 )/9)+h^2 ))) ⇒a=(√((1/2)(((4c^2 )/3)+h^2 −h(√(((8c^2 )/9)+h^2 )))))](https://www.tinkutara.com/question/Q65304.png)
$${R}={radius}\:{of}\:{circle} \\ $$$${d}\left(\mathrm{2}{R}−{d}\right)={c}^{\mathrm{2}} \\ $$$$\Rightarrow{R}=\frac{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }{\mathrm{2}{d}} \\ $$$${let}\:{h}={R}−{d}=\frac{{c}^{\mathrm{2}} −{d}^{\mathrm{2}} }{\mathrm{2}{d}} \\ $$$${eqn}.\:{of}\:{circle}: \\ $$$${x}^{\mathrm{2}} +\left({y}+{h}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{hy}+{h}^{\mathrm{2}} −{R}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{hy}−{c}^{\mathrm{2}} =\mathrm{0}\:\:\:\:…\left({i}\right) \\ $$$${eqn}.\:{of}\:{ellipse}: \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({y}−{b}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${x}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }{y}^{\mathrm{2}} −\frac{\mathrm{2}{a}^{\mathrm{2}} }{{b}}{y}=\mathrm{0}\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right){y}^{\mathrm{2}} +\mathrm{2}\left({h}+\frac{{a}^{\mathrm{2}} }{{b}}\right){y}−{c}^{\mathrm{2}} =\mathrm{0} \\ $$$${due}\:{to}\:{tangency}\:{there}\:{is}\:{only}\:{one}\:{root}, \\ $$$$\Delta=\mathrm{4}\left({h}+\frac{{a}^{\mathrm{2}} }{{b}}\right)^{\mathrm{2}} +\mathrm{4}{c}^{\mathrm{2}} \left(\mathrm{1}−\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$$\Rightarrow\left({hb}+{a}^{\mathrm{2}} \right)^{\mathrm{2}} +{c}^{\mathrm{2}} \left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)=\mathrm{0}\:\:…\left({iii}\right) \\ $$$$\Rightarrow\left({hab}+{a}^{\mathrm{3}} \right)^{\mathrm{2}} +{c}^{\mathrm{2}} \left({a}^{\mathrm{2}} {b}^{\mathrm{2}} −{a}^{\mathrm{4}} \right)=\mathrm{0} \\ $$$${let}\:{P}={ab} \\ $$$$\Rightarrow\left({hP}+{a}^{\mathrm{3}} \right)^{\mathrm{2}} +{c}^{\mathrm{2}} \left({P}^{\mathrm{2}} −{a}^{\mathrm{4}} \right)=\mathrm{0} \\ $$$${for}\:{maximum}\:{ellipse}\:{area},\:\frac{{dP}}{{da}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\left({hP}+{a}^{\mathrm{3}} \right)\left(\mathrm{3}{a}^{\mathrm{2}} \right)+{c}^{\mathrm{2}} \left(−\mathrm{4}{a}^{\mathrm{3}} \right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{3}\left({hb}+{a}^{\mathrm{2}} \right)−\mathrm{2}{c}^{\mathrm{2}} =\mathrm{0} \\ $$$${if}\:{h}=\mathrm{0},\:{i}.{e}.\:{d}={c}: \\ $$$$\mathrm{3}{a}^{\mathrm{2}} −\mathrm{2}{c}^{\mathrm{2}} =\mathrm{0}\Rightarrow{a}=\frac{\sqrt{\mathrm{6}}{c}}{\mathrm{3}}\Rightarrow{b}=\frac{\sqrt{\mathrm{2}}{c}}{\mathrm{3}} \\ $$$${if}\:{h}\neq\mathrm{0}: \\ $$$$\Rightarrow{b}=\frac{\mathrm{1}}{{h}}\left(\frac{\mathrm{2}{c}^{\mathrm{2}} }{\mathrm{3}}−{a}^{\mathrm{2}} \right) \\ $$$${insert}\:{this}\:{into}\:\left({iii}\right): \\ $$$$\left(\frac{\mathrm{2}{c}^{\mathrm{2}} }{\mathrm{3}}−{a}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} +{c}^{\mathrm{2}} \left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\frac{\mathrm{4}{c}^{\mathrm{2}} }{\mathrm{9}}+\frac{\mathrm{1}}{{h}^{\mathrm{2}} }\left(\frac{\mathrm{2}{c}^{\mathrm{2}} }{\mathrm{3}}−{a}^{\mathrm{2}} \right)^{\mathrm{2}} −{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{\mathrm{4}{c}^{\mathrm{2}} {h}^{\mathrm{2}} }{\mathrm{9}}+\left(\frac{\mathrm{2}{c}^{\mathrm{2}} }{\mathrm{3}}−{a}^{\mathrm{2}} \right)^{\mathrm{2}} −{h}^{\mathrm{2}} {a}^{\mathrm{2}} =\mathrm{0} \\ $$$${a}^{\mathrm{4}} −\left(\frac{\mathrm{4}{c}^{\mathrm{2}} }{\mathrm{3}}+{h}^{\mathrm{2}} \right){a}^{\mathrm{2}} +\frac{\mathrm{4}{c}^{\mathrm{2}} \left({c}^{\mathrm{2}} +{h}^{\mathrm{2}} \right)}{\mathrm{9}}=\mathrm{0} \\ $$$$\Rightarrow{a}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{4}{c}^{\mathrm{2}} }{\mathrm{3}}+{h}^{\mathrm{2}} −\sqrt{\left(\frac{\mathrm{4}{c}^{\mathrm{2}} }{\mathrm{3}}+{h}^{\mathrm{2}} \right)^{\mathrm{2}} −\frac{\mathrm{16}{c}^{\mathrm{2}} \left({c}^{\mathrm{2}} +{h}^{\mathrm{2}} \right)}{\mathrm{9}}}\right] \\ $$$$\Rightarrow{a}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{4}{c}^{\mathrm{2}} }{\mathrm{3}}+{h}^{\mathrm{2}} −\sqrt{\frac{\mathrm{16}{c}^{\mathrm{4}} +\mathrm{24}{c}^{\mathrm{2}} {h}^{\mathrm{2}} +\mathrm{9}{h}^{\mathrm{4}} −\mathrm{16}{c}^{\mathrm{4}} −\mathrm{16}{c}^{\mathrm{2}} {h}^{\mathrm{2}} }{\mathrm{9}}}\right] \\ $$$$\Rightarrow{a}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{4}{c}^{\mathrm{2}} }{\mathrm{3}}+{h}^{\mathrm{2}} −{h}\sqrt{\frac{\mathrm{8}{c}^{\mathrm{2}} }{\mathrm{9}}+{h}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{a}=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{4}{c}^{\mathrm{2}} }{\mathrm{3}}+{h}^{\mathrm{2}} −{h}\sqrt{\frac{\mathrm{8}{c}^{\mathrm{2}} }{\mathrm{9}}+{h}^{\mathrm{2}} }\right)} \\ $$
Commented by mr W last updated on 28/Jul/19