Question Number 65324 by hovea cw last updated on 28/Jul/19

Commented by mathmax by abdo last updated on 28/Jul/19
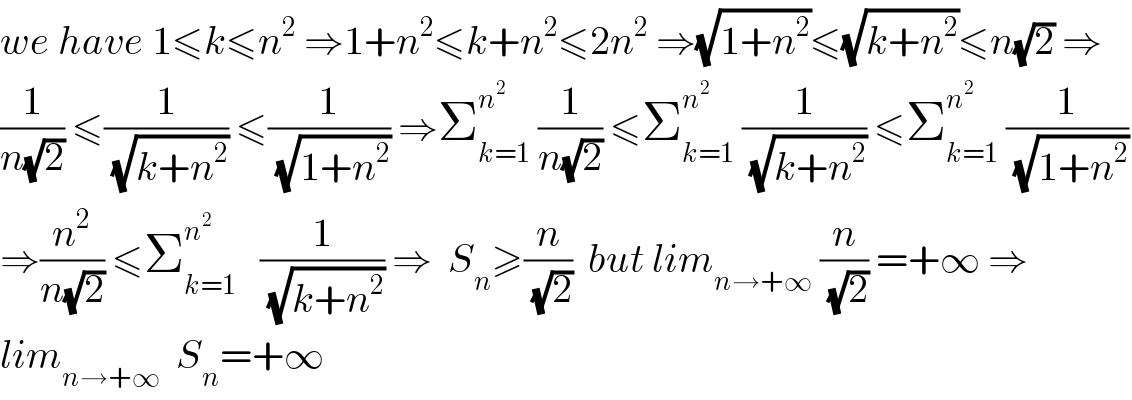
$${we}\:{have}\:\mathrm{1}\leqslant{k}\leqslant{n}^{\mathrm{2}} \:\Rightarrow\mathrm{1}+{n}^{\mathrm{2}} \leqslant{k}+{n}^{\mathrm{2}} \leqslant\mathrm{2}{n}^{\mathrm{2}} \:\Rightarrow\sqrt{\mathrm{1}+{n}^{\mathrm{2}} }\leqslant\sqrt{{k}+{n}^{\mathrm{2}} }\leqslant{n}\sqrt{\mathrm{2}}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{{n}\sqrt{\mathrm{2}}}\:\leqslant\frac{\mathrm{1}}{\:\sqrt{{k}+{n}^{\mathrm{2}} }}\:\leqslant\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{n}^{\mathrm{2}} }}\:\Rightarrow\sum_{{k}=\mathrm{1}} ^{{n}^{\mathrm{2}} } \:\frac{\mathrm{1}}{{n}\sqrt{\mathrm{2}}}\:\leqslant\sum_{{k}=\mathrm{1}} ^{{n}^{\mathrm{2}} \:} \:\frac{\mathrm{1}}{\:\sqrt{{k}+{n}^{\mathrm{2}} }}\:\leqslant\sum_{{k}=\mathrm{1}} ^{{n}^{\mathrm{2}} } \:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{n}^{\mathrm{2}} }} \\ $$$$\Rightarrow\frac{{n}^{\mathrm{2}} }{{n}\sqrt{\mathrm{2}}}\:\leqslant\sum_{{k}=\mathrm{1}} ^{{n}^{\mathrm{2}} } \:\:\:\frac{\mathrm{1}}{\:\sqrt{{k}+{n}^{\mathrm{2}} }}\:\Rightarrow\:\:{S}_{{n}} \geqslant\frac{{n}}{\:\sqrt{\mathrm{2}}}\:\:{but}\:{lim}_{{n}\rightarrow+\infty} \:\frac{{n}}{\:\sqrt{\mathrm{2}}}\:=+\infty\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:\:{S}_{{n}} =+\infty \\ $$
Commented by Cmr 237 last updated on 27/Aug/19

$$\mathrm{waouh}\:\mathrm{chapeau} \\ $$
Commented by mathmax by abdo last updated on 27/Aug/19

$${thanks}. \\ $$
