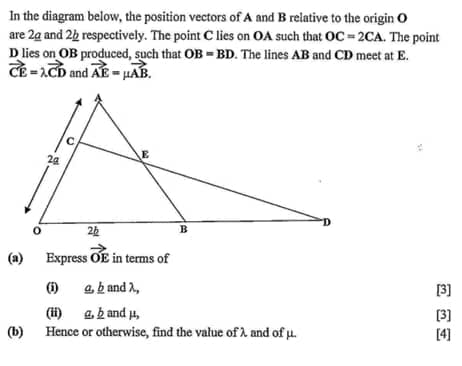
Question Number 65325 by Tawa1 last updated on 28/Jul/19
Commented by Tony Lin last updated on 28/Jul/19
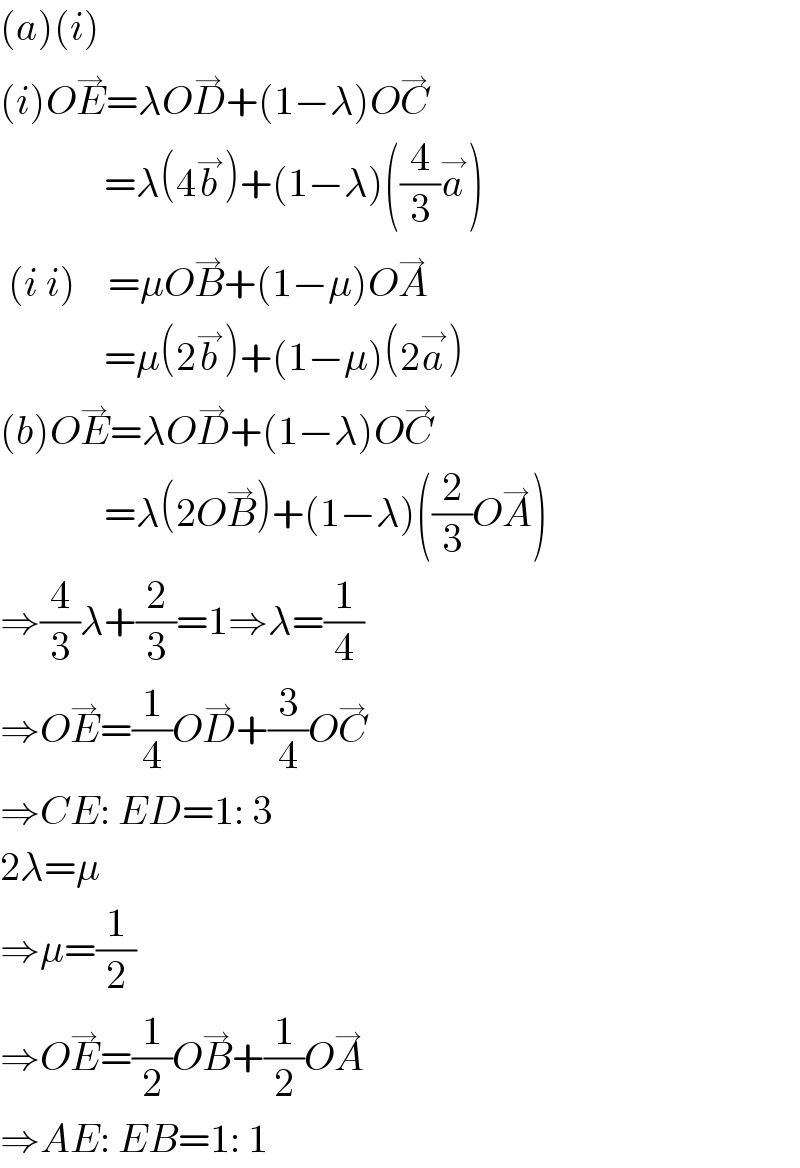
$$\left({a}\right)\left({i}\right) \\ $$$$\left({i}\right){O}\overset{\rightarrow} {{E}}=\lambda{O}\overset{\rightarrow} {{D}}+\left(\mathrm{1}−\lambda\right){O}\overset{\rightarrow} {{C}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\lambda\left(\mathrm{4}\overset{\rightarrow} {{b}}\right)+\left(\mathrm{1}−\lambda\right)\left(\frac{\mathrm{4}}{\mathrm{3}}\overset{\rightarrow} {{a}}\right) \\ $$$$\:\left({i}\:{i}\right)\:\:\:\:=\mu{O}\overset{\rightarrow} {{B}}+\left(\mathrm{1}−\mu\right){O}\overset{\rightarrow} {{A}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mu\left(\mathrm{2}\overset{\rightarrow} {{b}}\right)+\left(\mathrm{1}−\mu\right)\left(\mathrm{2}\overset{\rightarrow} {{a}}\right) \\ $$$$\left({b}\right){O}\overset{\rightarrow} {{E}}=\lambda{O}\overset{\rightarrow} {{D}}+\left(\mathrm{1}−\lambda\right){O}\overset{\rightarrow} {{C}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\lambda\left(\mathrm{2}{O}\overset{\rightarrow} {{B}}\right)+\left(\mathrm{1}−\lambda\right)\left(\frac{\mathrm{2}}{\mathrm{3}}{O}\overset{\rightarrow} {{A}}\right) \\ $$$$\Rightarrow\frac{\mathrm{4}}{\mathrm{3}}\lambda+\frac{\mathrm{2}}{\mathrm{3}}=\mathrm{1}\Rightarrow\lambda=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{O}\overset{\rightarrow} {{E}}=\frac{\mathrm{1}}{\mathrm{4}}{O}\overset{\rightarrow} {{D}}+\frac{\mathrm{3}}{\mathrm{4}}{O}\overset{\rightarrow} {{C}} \\ $$$$\Rightarrow{CE}:\:{ED}=\mathrm{1}:\:\mathrm{3} \\ $$$$\mathrm{2}\lambda=\mu \\ $$$$\Rightarrow\mu=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{O}\overset{\rightarrow} {{E}}=\frac{\mathrm{1}}{\mathrm{2}}{O}\overset{\rightarrow} {{B}}+\frac{\mathrm{1}}{\mathrm{2}}{O}\overset{\rightarrow} {{A}} \\ $$$$\Rightarrow{AE}:\:{EB}=\mathrm{1}:\:\mathrm{1} \\ $$
Commented by Tony Lin last updated on 28/Jul/19

$${or}\:{you}\:{can}\:{use}\:{Menelaus}\:{theorem} \\ $$$$\frac{{AC}}{{CO}}×\frac{{OD}}{{DB}}×\frac{{BE}}{{EA}}=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{1}}×\frac{{BE}}{{EA}}=\mathrm{1} \\ $$$$\Rightarrow{BE}:\:{EA}=\mathrm{1}:\:\mathrm{1} \\ $$$$\Rightarrow{O}\overset{\rightarrow} {{E}}=\frac{\mathrm{1}}{\mathrm{2}}{O}\overset{\rightarrow} {{A}}+\frac{\mathrm{1}}{\mathrm{2}}{O}\overset{\rightarrow} {{B}} \\ $$$$\Rightarrow\mu=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{DB}}{{BO}}×\frac{{OA}}{{AC}}×\frac{{CE}}{{ED}}=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}}×\frac{\mathrm{3}}{\mathrm{1}}×\frac{{CE}}{{ED}}=\mathrm{1} \\ $$$$\Rightarrow{CE}:\:{ED}=\mathrm{1}:\:\mathrm{3} \\ $$$$\Rightarrow{O}\overset{\rightarrow} {{E}}=\frac{\mathrm{1}}{\mathrm{4}}{O}\overset{\rightarrow} {{D}}+\frac{\mathrm{3}}{\mathrm{4}}{O}\overset{\rightarrow} {{C}} \\ $$$$\Rightarrow\lambda=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by Tawa1 last updated on 28/Jul/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time} \\ $$
Answered by mr W last updated on 28/Jul/19

$$\left({a}\right) \\ $$$$\left({i}\right) \\ $$$${CD}=−{CO}+{OD}=−\frac{\mathrm{4}}{\mathrm{3}}{a}+\mathrm{4}{b} \\ $$$${CE}=\lambda{CD}=−\frac{\mathrm{4}\lambda}{\mathrm{3}}{a}+\mathrm{4}\lambda{b} \\ $$$$\Rightarrow{OE}={OC}+{CE}=\frac{\mathrm{4}}{\mathrm{3}}{a}−\frac{\mathrm{4}\lambda}{\mathrm{3}}{a}+\mathrm{4}\lambda{b}=\frac{\mathrm{4}\left(\mathrm{1}−\lambda\right)}{\mathrm{3}}{a}+\mathrm{4}\lambda{b} \\ $$$$\left({ii}\right) \\ $$$${AB}={AO}+{OB}=−\mathrm{2}{a}+\mathrm{2}{b} \\ $$$${AE}=\mu{AB}=−\mathrm{2}\mu{a}+\mathrm{2}\mu{b} \\ $$$${OE}={OA}+{AE}=\mathrm{2}{a}−\mathrm{2}\mu{a}+\mathrm{2}\mu{b}=\mathrm{2}\left(\mathrm{1}−\mu\right){a}+\mathrm{2}\mu{b} \\ $$$$ \\ $$$$\left({b}\right) \\ $$$$\frac{\mathrm{4}\left(\mathrm{1}−\lambda\right)}{\mathrm{3}}=\mathrm{2}\left(\mathrm{1}−\mu\right) \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{1}−\lambda\right)=\mathrm{3}\left(\mathrm{1}−\mu\right) \\ $$$$\Rightarrow\mathrm{3}\mu−\mathrm{2}\lambda=\mathrm{1}\:\:\:\:\:\:…\left({i}\right) \\ $$$$\mathrm{4}\lambda=\mathrm{2}\mu \\ $$$$\Rightarrow\mathrm{2}\lambda−\mu=\mathrm{0}\:\:\:…\left({ii}\right) \\ $$$${from}\:\left({i}\right)\:{and}\:\left({ii}\right): \\ $$$$\mathrm{6}\lambda−\mathrm{2}\lambda=\mathrm{1} \\ $$$$\Rightarrow\lambda=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\mu=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Tawa1 last updated on 28/Jul/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time} \\ $$
