Question Number 65333 by aliesam last updated on 28/Jul/19
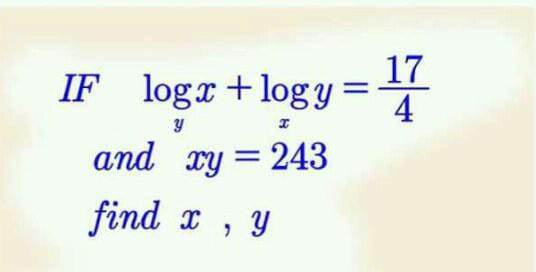
Commented by Prithwish sen last updated on 28/Jul/19
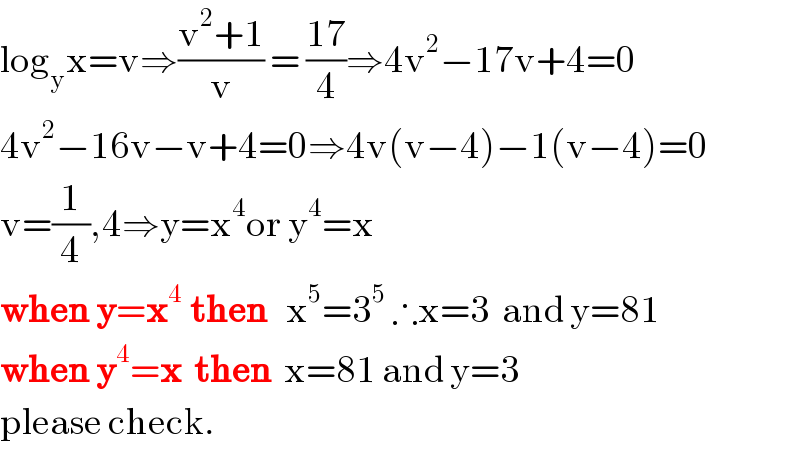
$$\mathrm{log}_{\mathrm{y}} \mathrm{x}=\mathrm{v}\Rightarrow\frac{\mathrm{v}^{\mathrm{2}} +\mathrm{1}}{\mathrm{v}}\:=\:\frac{\mathrm{17}}{\mathrm{4}}\Rightarrow\mathrm{4v}^{\mathrm{2}} −\mathrm{17v}+\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{4v}^{\mathrm{2}} −\mathrm{16v}−\mathrm{v}+\mathrm{4}=\mathrm{0}\Rightarrow\mathrm{4v}\left(\mathrm{v}−\mathrm{4}\right)−\mathrm{1}\left(\mathrm{v}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\mathrm{v}=\frac{\mathrm{1}}{\mathrm{4}},\mathrm{4}\Rightarrow\mathrm{y}=\mathrm{x}^{\mathrm{4}} \mathrm{or}\:\mathrm{y}^{\mathrm{4}} =\mathrm{x} \\ $$$$\boldsymbol{\mathrm{when}}\:\boldsymbol{\mathrm{y}}=\boldsymbol{\mathrm{x}}^{\mathrm{4}\:\:} \boldsymbol{\mathrm{then}}\:\:\:\mathrm{x}^{\mathrm{5}} =\mathrm{3}^{\mathrm{5}} \:\therefore\mathrm{x}=\mathrm{3}\:\:\mathrm{and}\:\mathrm{y}=\mathrm{81} \\ $$$$\boldsymbol{\mathrm{when}}\:\boldsymbol{\mathrm{y}}^{\mathrm{4}} =\boldsymbol{\mathrm{x}}\:\:\boldsymbol{\mathrm{then}}\:\:\mathrm{x}=\mathrm{81}\:\mathrm{and}\:\mathrm{y}=\mathrm{3} \\ $$$$\mathrm{please}\:\mathrm{check}. \\ $$
Answered by Tanmay chaudhury last updated on 28/Jul/19

$${log}_{{y}} {x}+{log}_{{x}} {y}=\frac{\mathrm{17}}{\mathrm{4}} \\ $$$${let}\:{logx}={a}\:\:\:{logy}={b} \\ $$$$\frac{{a}}{{b}}+\frac{{b}}{{a}}=\frac{\mathrm{17}}{\mathrm{4}} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} +\mathrm{4}{b}^{\mathrm{2}} −\mathrm{17}{ab}=\mathrm{0} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} −\mathrm{16}{ab}−{ab}+\mathrm{4}{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{4}{a}\left({a}−\mathrm{4}{b}\right)−{b}\left({a}−\mathrm{4}{b}\right)=\mathrm{0} \\ $$$$\left({a}−\mathrm{4}{b}\right)\left(\mathrm{4}{a}−{b}\right)=\mathrm{0} \\ $$$${a}=\mathrm{4}{b}\:\:{or}\:{a}=\frac{{b}}{\mathrm{4}} \\ $$$${when}\:{a}=\mathrm{4}{b} \\ $$$${logx}=\mathrm{4}{logy} \\ $$$${x}={y}^{\mathrm{4}} \\ $$$$\left({xy}\right)=\mathrm{243} \\ $$$$\left({y}^{\mathrm{5}} \right)=\mathrm{243}=\mathrm{3}^{\mathrm{5}} \\ $$$${y}=\mathrm{3}\:\:\:\:{and}\:\:{x}=\mathrm{3}^{\mathrm{4}} =\mathrm{81} \\ $$$${when}\:{a}=\frac{{b}}{\mathrm{4}} \\ $$$${logx}=\frac{{logy}}{\mathrm{4}} \\ $$$${y}={x}^{\mathrm{4}} \\ $$$$\left({xy}\right)=\mathrm{243} \\ $$$$\left({x}^{} ×{x}^{\mathrm{4}} \right)=\mathrm{243} \\ $$$${x}^{\mathrm{5}} =\mathrm{3}^{\mathrm{5}} \\ $$$${x}=\mathrm{3}\:\:\:\:\:{and}\:{y}=\mathrm{3}^{\mathrm{4}} =\mathrm{81} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{when}}\:\boldsymbol{{x}}=\mathrm{3}\:\:\:\boldsymbol{{y}}=\mathrm{81} \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{when}}\:\boldsymbol{{x}}=\mathrm{81}\:\:\:\boldsymbol{{y}}=\mathrm{3} \\ $$$$ \\ $$
