Question Number 65334 by Tawa1 last updated on 28/Jul/19
Answered by mr W last updated on 28/Jul/19
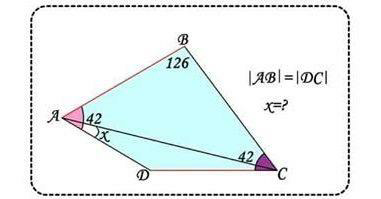
![∠D=360−126−42×2=150° ((DC)/(sin x))=((AC)/(sin 150)) ⇒DC=((sin x)/(sin 150))×AC ((AC)/(sin 126))=((AB)/(sin [42−(30−x)]))=((AB)/(sin (x+12))) ⇒AB=((sin (x+12))/(sin 126))×AC DC=AB ⇒((sin x)/(sin 150))=((sin (x+12))/(sin 126)) ⇒((sin x)/(sin 30))=((sin x cos 12+cos x sin 12)/(sin 54)) ⇒(1/(sin 30))=((cos 12+cot x sin 12)/(cos 36)) ⇒cot x=((2 cos 36−cos 12)/(sin 12)) ⇒cot x=(((8 cos^2 12−7)cos 12)/(sin 12)) ⇒cot x=((1−8 sin^2 12)/(tan 12)) ⇒x=18°](https://www.tinkutara.com/question/Q65340.png)
$$\angle{D}=\mathrm{360}−\mathrm{126}−\mathrm{42}×\mathrm{2}=\mathrm{150}° \\ $$$$\frac{{DC}}{\mathrm{sin}\:{x}}=\frac{{AC}}{\mathrm{sin}\:\mathrm{150}} \\ $$$$\Rightarrow{DC}=\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:\mathrm{150}}×{AC} \\ $$$$\frac{{AC}}{\mathrm{sin}\:\mathrm{126}}=\frac{{AB}}{\mathrm{sin}\:\left[\mathrm{42}−\left(\mathrm{30}−{x}\right)\right]}=\frac{{AB}}{\mathrm{sin}\:\left({x}+\mathrm{12}\right)} \\ $$$$\Rightarrow{AB}=\frac{\mathrm{sin}\:\left({x}+\mathrm{12}\right)}{\mathrm{sin}\:\mathrm{126}}×{AC} \\ $$$${DC}={AB} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:\mathrm{150}}=\frac{\mathrm{sin}\:\left({x}+\mathrm{12}\right)}{\mathrm{sin}\:\mathrm{126}} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:\mathrm{30}}=\frac{\mathrm{sin}\:{x}\:\mathrm{cos}\:\mathrm{12}+\mathrm{cos}\:{x}\:\mathrm{sin}\:\mathrm{12}}{\mathrm{sin}\:\mathrm{54}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{30}}=\frac{\mathrm{cos}\:\mathrm{12}+\mathrm{cot}\:{x}\:\mathrm{sin}\:\mathrm{12}}{\mathrm{cos}\:\mathrm{36}} \\ $$$$\Rightarrow\mathrm{cot}\:{x}=\frac{\mathrm{2}\:\mathrm{cos}\:\mathrm{36}−\mathrm{cos}\:\mathrm{12}}{\mathrm{sin}\:\mathrm{12}} \\ $$$$\Rightarrow\mathrm{cot}\:{x}=\frac{\left(\mathrm{8}\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{12}−\mathrm{7}\right)\mathrm{cos}\:\mathrm{12}}{\mathrm{sin}\:\mathrm{12}} \\ $$$$\Rightarrow\mathrm{cot}\:{x}=\frac{\mathrm{1}−\mathrm{8}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{12}}{\mathrm{tan}\:\mathrm{12}} \\ $$$$\Rightarrow{x}=\mathrm{18}° \\ $$
Commented by Tawa1 last updated on 28/Jul/19
$$\mathrm{Great}\:\mathrm{sir},\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}.\:\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}. \\ $$
Commented by Tony Lin last updated on 29/Jul/19
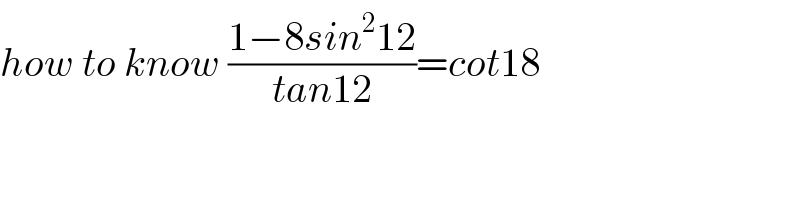
$${how}\:{to}\:{know}\:\frac{\mathrm{1}−\mathrm{8}{sin}^{\mathrm{2}} \mathrm{12}}{{tan}\mathrm{12}}={cot}\mathrm{18} \\ $$
