Menu Close

Question-65490

Tinku Tara 0 Comments
Pin




Question Number 65490 by Masumsiddiqui399@gmail.com last updated on 30/Jul/19
Commented by mathmax by abdo last updated on 31/Jul/19
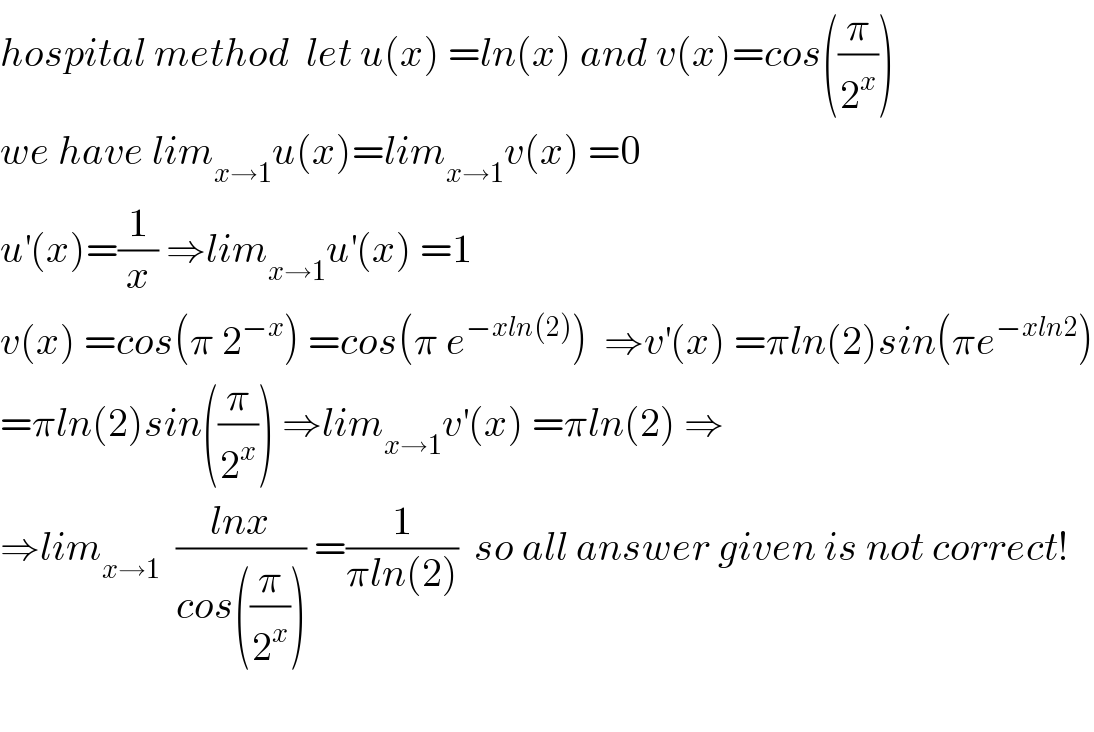
hospital method let u(x) =ln(x) and v(x)=cos((π/2^x )) we have lim_(x→1) u(x)=lim_(x→1) v(x) =0 u^′ (x)=(1/x) ⇒lim_(x→1) u^′ (x) =1 v(x) =cos(π 2^(−x) ) =cos(π e^(−xln(2)) ) ⇒v^′ (x) =πln(2)sin(πe^(−xln2) ) =πln(2)sin((π/2^x )) ⇒lim_(x→1) v^′ (x) =πln(2) ⇒ ⇒lim_(x→1) ((lnx)/(cos((π/2^x )))) =(1/(πln(2))) so all answer given is not correct!
$${hospital}\:{method}\:\:{let}\:{u}\left({x}\right)\:={ln}\left({x}\right)\:{and}\:{v}\left({x}\right)={cos}\left(\frac{\pi}{\mathrm{2}^{{x}} }\right) \\ $$$${we}\:{have}\:{lim}_{{x}\rightarrow\mathrm{1}} {u}\left({x}\right)={lim}_{{x}\rightarrow\mathrm{1}} {v}\left({x}\right)\:=\mathrm{0} \\ $$$${u}^{'} \left({x}\right)=\frac{\mathrm{1}}{{x}}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{1}} {u}^{'} \left({x}\right)\:=\mathrm{1} \\ $$$${v}\left({x}\right)\:={cos}\left(\pi\:\mathrm{2}^{−{x}} \right)\:={cos}\left(\pi\:{e}^{−{xln}\left(\mathrm{2}\right)} \right)\:\:\Rightarrow{v}^{'} \left({x}\right)\:=\pi{ln}\left(\mathrm{2}\right){sin}\left(\pi{e}^{−{xln}\mathrm{2}} \right) \\ $$$$=\pi{ln}\left(\mathrm{2}\right){sin}\left(\frac{\pi}{\mathrm{2}^{{x}} }\right)\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{1}} {v}^{'} \left({x}\right)\:=\pi{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\Rightarrow{lim}_{{x}\rightarrow\mathrm{1}} \:\:\frac{{lnx}}{{cos}\left(\frac{\pi}{\mathrm{2}^{{x}} }\right)}\:=\frac{\mathrm{1}}{\pi{ln}\left(\mathrm{2}\right)}\:\:{so}\:{all}\:{answer}\:{given}\:{is}\:{not}\:{correct}! \\ $$$$ \\ $$
Commented by MJS last updated on 31/Jul/19
lim_(x→1) ((ln x)/(cos (π/2^x ))) =lim_(x→1) (((d/dx)[ln x])/((d/dx)[cos (π/2^x )])) =lim_(x→1) ((1/x)/(((πln 2)/2^x )sin (π/2^x ))) = =lim_(x→1) (2^x /(πln 2 xsin (π/2^x ) ))=(2/(πln 2))
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{ln}\:{x}}{\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{{x}} }}\:=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\frac{{d}}{{dx}}\left[\mathrm{ln}\:{x}\right]}{\frac{{d}}{{dx}}\left[\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{{x}} }\right]}\:=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{{x}}}{\frac{\pi\mathrm{ln}\:\mathrm{2}}{\mathrm{2}^{{x}} }\mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{x}} }}\:= \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{2}^{{x}} }{\pi\mathrm{ln}\:\mathrm{2}\:{x}\mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{x}} }\:}=\frac{\mathrm{2}}{\pi\mathrm{ln}\:\mathrm{2}} \\ $$
Commented by mathmax by abdo last updated on 31/Jul/19
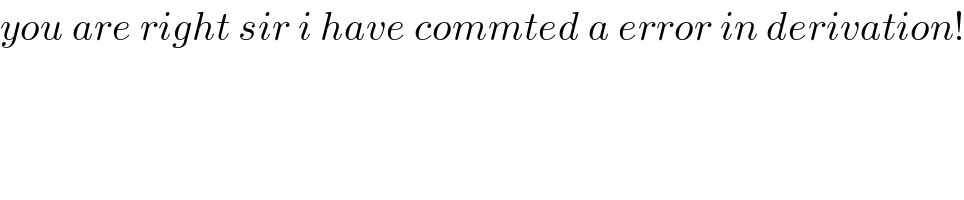
you are right sir i have commted a error in derivation!
$${you}\:{are}\:{right}\:{sir}\:{i}\:{have}\:{commted}\:{a}\:{error}\:{in}\:{derivation}! \\ $$
Commented by mathmax by abdo last updated on 31/Jul/19
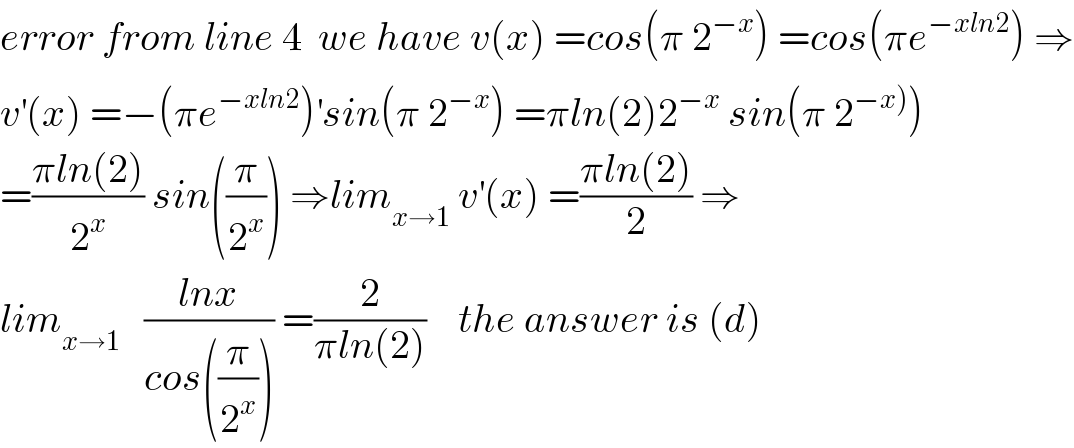
error from line 4 we have v(x) =cos(π 2^(−x) ) =cos(πe^(−xln2) ) ⇒ v^′ (x) =−(πe^(−xln2) )^′ sin(π 2^(−x) ) =πln(2)2^(−x) sin(π 2^(−x)) ) =((πln(2))/2^x ) sin((π/2^x )) ⇒lim_(x→1) v^′ (x) =((πln(2))/2) ⇒ lim_(x→1) ((lnx)/(cos((π/2^x )))) =(2/(πln(2))) the answer is (d)
$${error}\:{from}\:{line}\:\mathrm{4}\:\:{we}\:{have}\:{v}\left({x}\right)\:={cos}\left(\pi\:\mathrm{2}^{−{x}} \right)\:={cos}\left(\pi{e}^{−{xln}\mathrm{2}} \right)\:\Rightarrow \\ $$$${v}^{'} \left({x}\right)\:=−\left(\pi{e}^{−{xln}\mathrm{2}} \right)^{'} {sin}\left(\pi\:\mathrm{2}^{−{x}} \right)\:=\pi{ln}\left(\mathrm{2}\right)\mathrm{2}^{−{x}} \:{sin}\left(\pi\:\mathrm{2}^{\left.−{x}\right)} \right) \\ $$$$=\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{2}^{{x}} }\:{sin}\left(\frac{\pi}{\mathrm{2}^{{x}} }\right)\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{1}} \:{v}^{'} \left({x}\right)\:=\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{1}} \:\:\:\frac{{lnx}}{{cos}\left(\frac{\pi}{\mathrm{2}^{{x}} }\right)}\:=\frac{\mathrm{2}}{\pi{ln}\left(\mathrm{2}\right)}\:\:\:\:{the}\:{answer}\:{is}\:\left({d}\right) \\ $$
Commented by mathmax by abdo last updated on 31/Jul/19
let try another way we use the changement x−1 =t ⇒ ((ln(x))/(cos((π/2^x )))) =((ln(1+t))/(cos((π/2^(1+t) )))) [wehave x→1 ⇔t→0 ln^′ (1+t)=(1/(1+t)) =1−t +o(t^2 ) ⇒ln(1+t) =t−(t^2 /2) +o(t^3 ) cos((π/2^(1+t) )) =cos((π/2) 2^(−t) ) =cos(((πα)/2)) (α →1) α =1+u and u→0 ⇒cos(((πα)/2))=cos((π/2)(1+u)) =cos((π/2) +(π/2)u) =−sin((π/2)u) ∼−(π/2)u =−(π/2)(α−1)=−(π/2)(2^(−t) −1) =(π/2)(1−2^(−t) ) =(π/2)(1−e^(−tln(2)) ) ∼(π/2)(1−(1−tln(2)) =(π/2)(tln(2)) ⇒((ln(1+t))/(cos((π/2^(1+t) )))) ∼ ((t−(t^2 /2))/((π/2)(tln2))) =((1−(t/2))/((πln2)/2)) →(2/(πln(2)))(t→0)
$${let}\:{try}\:{another}\:{way}\:\:{we}\:{use}\:{the}\:{changement}\:{x}−\mathrm{1}\:={t}\:\Rightarrow \\ $$$$\frac{{ln}\left({x}\right)}{{cos}\left(\frac{\pi}{\mathrm{2}^{{x}} }\right)}\:=\frac{{ln}\left(\mathrm{1}+{t}\right)}{{cos}\left(\frac{\pi}{\mathrm{2}^{\mathrm{1}+{t}} }\right)}\:\left[{wehave}\:{x}\rightarrow\mathrm{1}\:\Leftrightarrow{t}\rightarrow\mathrm{0}\right. \\ $$$${ln}^{'} \left(\mathrm{1}+{t}\right)=\frac{\mathrm{1}}{\mathrm{1}+{t}}\:=\mathrm{1}−{t}\:+{o}\left({t}^{\mathrm{2}} \right)\:\Rightarrow{ln}\left(\mathrm{1}+{t}\right)\:={t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:+{o}\left({t}^{\mathrm{3}} \right) \\ $$$${cos}\left(\frac{\pi}{\mathrm{2}^{\mathrm{1}+{t}} }\right)\:={cos}\left(\frac{\pi}{\mathrm{2}}\:\mathrm{2}^{−{t}} \right)\:={cos}\left(\frac{\pi\alpha}{\mathrm{2}}\right)\:\:\:\left(\alpha\:\rightarrow\mathrm{1}\right) \\ $$$$\alpha\:=\mathrm{1}+{u}\:\:\:{and}\:{u}\rightarrow\mathrm{0}\:\Rightarrow{cos}\left(\frac{\pi\alpha}{\mathrm{2}}\right)={cos}\left(\frac{\pi}{\mathrm{2}}\left(\mathrm{1}+{u}\right)\right) \\ $$$$={cos}\left(\frac{\pi}{\mathrm{2}}\:+\frac{\pi}{\mathrm{2}}{u}\right)\:=−{sin}\left(\frac{\pi}{\mathrm{2}}{u}\right)\:\:\sim−\frac{\pi}{\mathrm{2}}{u}\:=−\frac{\pi}{\mathrm{2}}\left(\alpha−\mathrm{1}\right)=−\frac{\pi}{\mathrm{2}}\left(\mathrm{2}^{−{t}} −\mathrm{1}\right) \\ $$$$=\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\mathrm{2}^{−{t}} \right)\:=\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−{e}^{−{tln}\left(\mathrm{2}\right)} \right)\:\sim\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\left(\mathrm{1}−{tln}\left(\mathrm{2}\right)\right)\right. \\ $$$$=\frac{\pi}{\mathrm{2}}\left({tln}\left(\mathrm{2}\right)\right)\:\Rightarrow\frac{{ln}\left(\mathrm{1}+{t}\right)}{{cos}\left(\frac{\pi}{\mathrm{2}^{\mathrm{1}+{t}} }\right)}\:\sim\:\:\frac{{t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}}{\frac{\pi}{\mathrm{2}}\left({tln}\mathrm{2}\right)}\:=\frac{\mathrm{1}−\frac{{t}}{\mathrm{2}}}{\frac{\pi{ln}\mathrm{2}}{\mathrm{2}}}\:\rightarrow\frac{\mathrm{2}}{\pi{ln}\left(\mathrm{2}\right)}\left({t}\rightarrow\mathrm{0}\right) \\ $$
Commented by MJS last updated on 31/Jul/19
well, it was just a tiny error, I use to make these too sometimes... it seems the mind is faster than the typing fingers.
$$\mathrm{well},\:\mathrm{it}\:\mathrm{was}\:\mathrm{just}\:\mathrm{a}\:\mathrm{tiny}\:\mathrm{error},\:\mathrm{I}\:\mathrm{use}\:\mathrm{to}\:\mathrm{make} \\ $$$$\mathrm{these}\:\mathrm{too}\:\mathrm{sometimes}…\:\mathrm{it}\:\mathrm{seems}\:\mathrm{the}\:\mathrm{mind}\:\mathrm{is} \\ $$$$\mathrm{faster}\:\mathrm{than}\:\mathrm{the}\:\mathrm{typing}\:\mathrm{fingers}. \\ $$
Commented by mathmax by abdo last updated on 31/Jul/19
yes you are right sir the mind always detect the error...
$${yes}\:{you}\:{are}\:{right}\:{sir}\:{the}\:{mind}\:{always}\:{detect}\:{the}\:{error}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *