Question Number 78650 by Pratah last updated on 19/Jan/20

Commented by mr W last updated on 19/Jan/20

$$={x}^{\mathrm{2}} +\mathrm{1} \\ $$
Commented by john santu last updated on 20/Jan/20

$${sorry}\:{sir},\:{yesterday}\:{already}\: \\ $$$${slept} \\ $$
Commented by Pratah last updated on 19/Jan/20

$$\mathrm{sir}\:\mathrm{john}\:\mathrm{santu} \\ $$
Commented by Pratah last updated on 19/Jan/20

$$\mathrm{please} \\ $$
Answered by mind is power last updated on 19/Jan/20
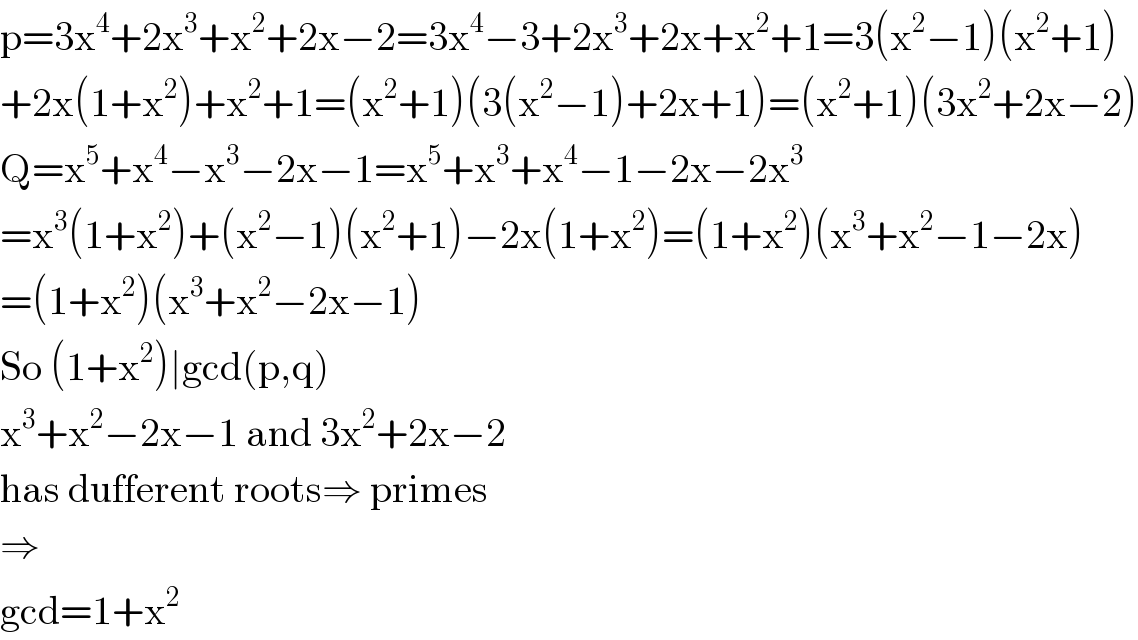
$$\mathrm{p}=\mathrm{3x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{2}=\mathrm{3x}^{\mathrm{4}} −\mathrm{3}+\mathrm{2x}^{\mathrm{3}} +\mathrm{2x}+\mathrm{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{3}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$+\mathrm{2x}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)+\mathrm{x}^{\mathrm{2}} +\mathrm{1}=\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{3}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{2x}+\mathrm{1}\right)=\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{3x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{2}\right) \\ $$$$\mathrm{Q}=\mathrm{x}^{\mathrm{5}} +\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{3}} −\mathrm{2x}−\mathrm{1}=\mathrm{x}^{\mathrm{5}} +\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{4}} −\mathrm{1}−\mathrm{2x}−\mathrm{2x}^{\mathrm{3}} \\ $$$$=\mathrm{x}^{\mathrm{3}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)+\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{2x}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)=\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{1}−\mathrm{2x}\right) \\ $$$$=\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{1}\right) \\ $$$$\mathrm{So}\:\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mid\mathrm{gcd}\left(\mathrm{p},\mathrm{q}\right) \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{1}\:\mathrm{and}\:\mathrm{3x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{2}\: \\ $$$$\mathrm{has}\:\mathrm{dufferent}\:\mathrm{roots}\Rightarrow\:\mathrm{primes} \\ $$$$\Rightarrow \\ $$$$\mathrm{gcd}=\mathrm{1}+\mathrm{x}^{\mathrm{2}} \\ $$
Commented by Pratah last updated on 19/Jan/20

$$\mathrm{thanks} \\ $$
Answered by Rasheed.Sindhi last updated on 19/Jan/20

$$\mathrm{gcd}\left(\mathrm{x}^{\mathrm{5}} +\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{3}} −\mathrm{2x}−\mathrm{1},\mathrm{3x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{2}\right) \\ $$$$=\mathrm{gcd}\left(\mathrm{3}\left(\mathrm{x}^{\mathrm{5}} +\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{3}} −\mathrm{2x}−\mathrm{1}\right),\mathrm{3x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{2}\right) \\ $$$$\begin{vmatrix}{}&{\mathrm{x}+\mathrm{1}}\\{\left.\mathrm{3x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{2}\right)}&{+\mathrm{3x}^{\mathrm{5}} +\mathrm{3x}^{\mathrm{4}} −\mathrm{3x}^{\mathrm{3}} +\mathrm{0x}^{\mathrm{2}} −\mathrm{6x}−\mathrm{3}}\\{}&{\underset{−} {+}\mathrm{3x}^{\mathrm{5}} \underset{−} {+}\mathrm{2x}^{\mathrm{4}} \underset{−} {+}\:\:\:\mathrm{x}^{\mathrm{3}} \underset{−} {+}\mathrm{2x}^{\mathrm{2}} \underset{+} {−}\mathrm{2x}}\\{}&{\mathrm{3}\left(\mathrm{x}^{\mathrm{4}} −\mathrm{4x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} −\mathrm{4x}−\mathrm{3}\right)}\\{}&{=\mathrm{3x}^{\mathrm{4}} −\mathrm{12x}^{\mathrm{3}} −\mathrm{6x}^{\mathrm{2}} −\mathrm{12x}−\mathrm{9}}\\{}&{\underset{−} {+}\mathrm{3x}^{\mathrm{4}} \underset{−} {+}\:\:\:\mathrm{2x}^{\mathrm{3}} \underset{−} {+}\:\:\:\:\mathrm{x}^{\mathrm{2}} \underset{−} {+}\:\:\:\mathrm{2x}\underset{+} {−}\mathrm{2}}\\{}&{−\mathrm{14x}^{\mathrm{3}} −\mathrm{7x}^{\mathrm{2}} −\mathrm{14x}−\mathrm{7}}\\{}&{=−\mathrm{7}\left(\mathrm{2x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}\right)}\end{vmatrix} \\ $$$$ \\ $$$$\begin{vmatrix}{}&{\mathrm{x}+\mathrm{1}}\\{\left.\mathrm{6x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{3}\right)}&{+\mathrm{6x}^{\mathrm{4}} +\mathrm{4x}^{\mathrm{3}} +\mathrm{2x}^{\mathrm{2}} +\mathrm{4x}−\mathrm{4}}\\{}&{\underset{−} {+}\mathrm{6x}^{\mathrm{4}} \underset{−} {+}\mathrm{3x}^{\mathrm{3}} \underset{−} {+}\mathrm{6x}^{\mathrm{2}} \underset{−} {+}\mathrm{3x}}\\{}&{\mathrm{x}^{\mathrm{3}} −\mathrm{4x}^{\mathrm{2}} +\mathrm{x}−\mathrm{4}}\\{}&{\mathrm{6}\left(\mathrm{x}^{\mathrm{3}} −\mathrm{4x}^{\mathrm{2}} +\mathrm{x}−\mathrm{4}\right)}\\{}&{=\mathrm{6x}^{\mathrm{3}} −\mathrm{24x}^{\mathrm{2}} +\mathrm{6x}−\mathrm{24}}\\{}&{\underset{−} {+}\mathrm{6x}^{\mathrm{3}} \underset{−} {+}\mathrm{3x}^{\mathrm{2}} \underset{−} {+}\mathrm{6x}\underset{−} {+}\mathrm{3}}\\{}&{−\mathrm{27x}^{\mathrm{2}} −\mathrm{27}}\\{}&{=−\mathrm{27}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}\end{vmatrix} \\ $$$$ \\ $$$$\begin{vmatrix}{}&{\mathrm{6x}+\mathrm{3}}\\{\left.\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}&{\:\:\:\:\mathrm{6x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{3}}\\{}&{\underset{−} {+}\mathrm{6x}^{\mathrm{3}} \:\:\:\:\:\:\:\:\:\:\:\underset{−} {+}\mathrm{6x}}\\{}&{\:\:\:\:\mathrm{3x}^{\mathrm{2}} +\mathrm{3}}\\{}&{\underset{−} {+}\mathrm{3x}^{\mathrm{2}} \underset{−} {+}\mathrm{3}}\\{}&{\mathrm{0}}\end{vmatrix} \\ $$$$\mathrm{gcd}=\mathrm{x}^{\mathrm{2}} +\mathrm{1} \\ $$
Commented by Pratah last updated on 19/Jan/20

$$\mathrm{great} \\ $$
