Question-78799

Question Number 78799 by Pratah last updated on 20/Jan/20

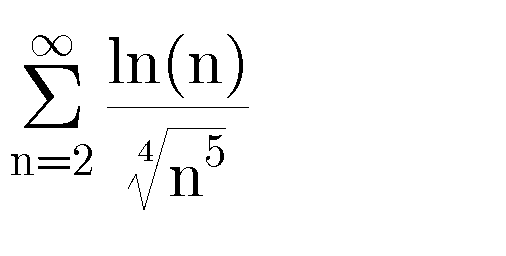
Commented by mathmax by abdo last updated on 20/Jan/20

convergence? let f(x)=((ln(x))/x^(5/4) ) with x≥2 we have f^′ (x)=(((1/x)x^(5/4) −(5/4)x^((5/4)−1) lnx)/x^(5/2) ) =((x^((5/4)−1) −(5/4)x^((5/4)−1) lnx)/x^(5/2) ) =(x^(1/4) /x^(5/2) )×(1−(5/4)lnx) =((1−(5/4)ln(x))/x^((5/2)−(1/4)) ) =((4−5lnx)/(4 x^(9/4) )) 4−5lnx <0 ⇔4<5lnx ⇒lnx>(4/5) ⇒x >e^(4/5) so for x>e^(4/5) f^′ <0 ⇒f is decreazing ⇒Σ_(n=2) ^∞ ((lnn)/n^(5/4) ) and ∫_2 ^(+∞) ((lnx)/x^(5/4) )dx have the same nature of conv. changement ln(x)=t give ∫_2 ^(+∞) ((lnx)/x^(5/4) )dx =∫_(ln(2)) ^(+∞) (t/((e^t )^(5/4) )) e^t dt =∫_2 ^(+∞) t e^(t−(5/4)t) dt =∫_2 ^(+∞) t e^(−(t/4)) dt and this integral is convergengent ⇒this serie is convergent.

$${convergence}?\:\:\:{let}\:{f}\left({x}\right)=\frac{{ln}\left({x}\right)}{{x}^{\frac{\mathrm{5}}{\mathrm{4}}} }\:\:\:{with}\:{x}\geqslant\mathrm{2}\:\:{we}\:{have} \\ $$$${f}^{'} \left({x}\right)=\frac{\frac{\mathrm{1}}{{x}}{x}^{\frac{\mathrm{5}}{\mathrm{4}}} −\frac{\mathrm{5}}{\mathrm{4}}{x}^{\frac{\mathrm{5}}{\mathrm{4}}−\mathrm{1}} {lnx}}{{x}^{\frac{\mathrm{5}}{\mathrm{2}}} }\:=\frac{{x}^{\frac{\mathrm{5}}{\mathrm{4}}−\mathrm{1}} −\frac{\mathrm{5}}{\mathrm{4}}{x}^{\frac{\mathrm{5}}{\mathrm{4}}−\mathrm{1}} {lnx}}{{x}^{\frac{\mathrm{5}}{\mathrm{2}}} } \\ $$$$=\frac{{x}^{\frac{\mathrm{1}}{\mathrm{4}}} }{{x}^{\frac{\mathrm{5}}{\mathrm{2}}} }×\left(\mathrm{1}−\frac{\mathrm{5}}{\mathrm{4}}{lnx}\right)\:=\frac{\mathrm{1}−\frac{\mathrm{5}}{\mathrm{4}}{ln}\left({x}\right)}{{x}^{\frac{\mathrm{5}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}} }\:=\frac{\mathrm{4}−\mathrm{5}{lnx}}{\mathrm{4}\:{x}^{\frac{\mathrm{9}}{\mathrm{4}}} } \\ $$$$\mathrm{4}−\mathrm{5}{lnx}\:<\mathrm{0}\:\Leftrightarrow\mathrm{4}<\mathrm{5}{lnx}\:\Rightarrow{lnx}>\frac{\mathrm{4}}{\mathrm{5}}\:\Rightarrow{x}\:>{e}^{\frac{\mathrm{4}}{\mathrm{5}}} \\ $$$${so}\:{for}\:{x}>{e}^{\frac{\mathrm{4}}{\mathrm{5}}} \:\:\:{f}^{'} <\mathrm{0}\:\Rightarrow{f}\:{is}\:{decreazing}\:\Rightarrow\sum_{{n}=\mathrm{2}} ^{\infty} \frac{{lnn}}{{n}^{\frac{\mathrm{5}}{\mathrm{4}}} }\:{and} \\ $$$$\int_{\mathrm{2}} ^{+\infty} \:\frac{{lnx}}{{x}^{\frac{\mathrm{5}}{\mathrm{4}}} }{dx}\:\:{have}\:{the}\:{same}\:{nature}\:{of}\:{conv}.\:{changement} \\ $$$${ln}\left({x}\right)={t}\:{give}\:\int_{\mathrm{2}} ^{+\infty} \:\frac{{lnx}}{{x}^{\frac{\mathrm{5}}{\mathrm{4}}} }{dx}\:=\int_{{ln}\left(\mathrm{2}\right)} ^{+\infty} \:\frac{{t}}{\left({e}^{{t}} \right)^{\frac{\mathrm{5}}{\mathrm{4}}} }\:{e}^{{t}} \:{dt} \\ $$$$=\int_{\mathrm{2}} ^{+\infty} \:\:{t}\:{e}^{{t}−\frac{\mathrm{5}}{\mathrm{4}}{t}} \:{dt}\:\:=\int_{\mathrm{2}} ^{+\infty} \:{t}\:\:{e}^{−\frac{{t}}{\mathrm{4}}} \:{dt}\:\:{and}\:{this}\:{integral}\:{is}\:{convergengent} \\ $$$$\Rightarrow{this}\:{serie}\:{is}\:{convergent}. \\ $$

Commented by mind is power last updated on 20/Jan/20