Menu Close

Question-79004

Tinku Tara 0 Comments
Pin




Question Number 79004 by mr W last updated on 22/Jan/20
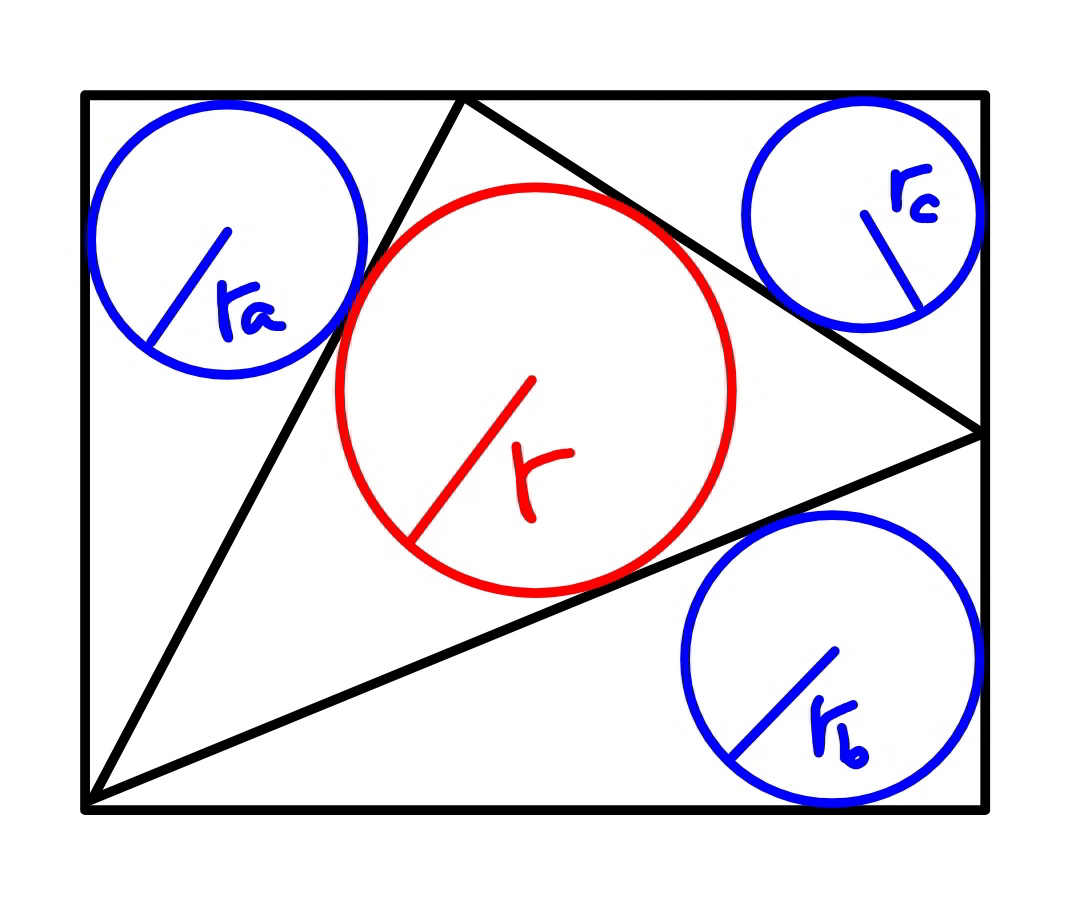
Commented by mr W last updated on 22/Jan/20
In a rectangle the radii r_a ,r_b ,r_c are given. Find the radius r of the fourth circle.
$${In}\:{a}\:{rectangle}\:{the}\:{radii}\:{r}_{{a}} ,{r}_{{b}} ,{r}_{{c}} \:{are} \\ $$$${given}.\:{Find}\:{the}\:{radius}\:{r}\:{of}\:{the} \\ $$$${fourth}\:{circle}. \\ $$
Commented by jagoll last updated on 22/Jan/20
using theorem Leibniz sir?
$$\mathrm{using}\:\mathrm{theorem}\:\mathrm{Leibniz}\:\mathrm{sir}? \\ $$
Commented by mr W last updated on 22/Jan/20
you can use what you like.
$${you}\:{can}\:{use}\:{what}\:{you}\:{like}. \\ $$
Answered by mind is power last updated on 22/Jan/20
i Will poste a complete Solution first idea ABC rectangle in B ,a=BC,b=AC,c=BA rayon of inscrit Circle ABC R=((ac)/(a+b+c)) put equation R_a , R_b ,R_c find Sides of Triangle withe circl Radius r
$${i}\:{Will}\:{poste}\:{a}\:{complete}\:{Solution}\:{first}\:{idea} \\ $$$${ABC}\:{rectangle}\:{in}\:{B}\:,{a}={BC},{b}={AC},{c}={BA} \\ $$$${rayon}\:{of}\:{inscrit}\:{Circle}\:{ABC}\:{R}=\frac{{ac}}{{a}+{b}+{c}} \\ $$$${put}\:{equation}\:{R}_{{a}} \:,\:{R}_{{b}} ,{R}_{{c}} \\ $$$$\:{find}\:{Sides}\:{of}\:\:{Triangle}\:{withe}\:{circl}\:{Radius}\:{r} \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 22/Jan/20
thanks for your interest sir! it seems that the radius of the fourth circle can not be determined with given conditions uniquely.
$${thanks}\:{for}\:{your}\:{interest}\:{sir}!\:{it}\:{seems} \\ $$$${that}\:{the}\:{radius}\:{of}\:{the}\:{fourth}\:{circle}\:{can} \\ $$$${not}\:{be}\:{determined}\:{with}\:{given}\:{conditions} \\ $$$${uniquely}. \\ $$
Answered by mr W last updated on 22/Jan/20
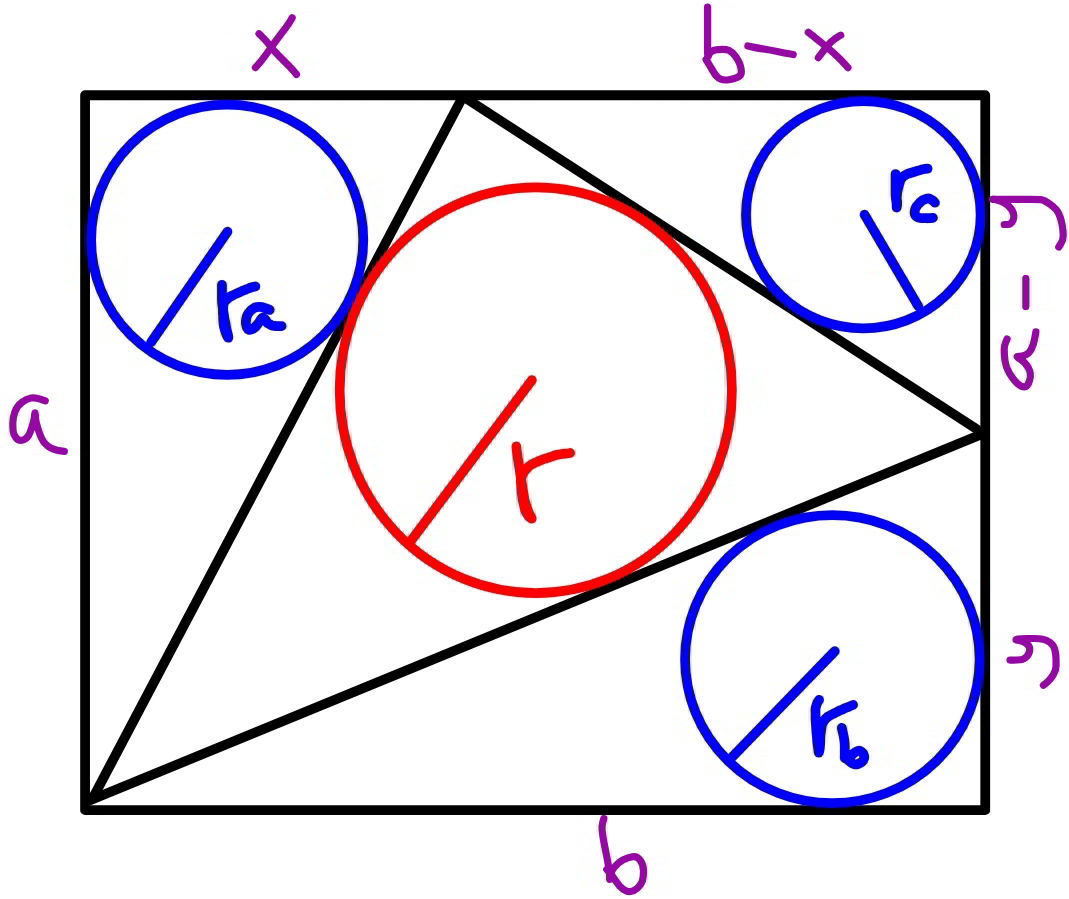
Commented by mr W last updated on 22/Jan/20
an attempt... ax=r_a (a+x+(√(a^2 +x^2 ))) by=r_b (b+y+(√(b^2 +y^2 ))) (b−x)(a−y)=r_c [(b−x)+(a−y)+(√((b−x)^2 +(a−y)^2 ))] 2ab−ax−by−(b−x)(a−y)=r[(√(a^2 +x^2 ))+(√(b^2 +y^2 ))+(√((b−x)^2 +(a−y)^2 ))] ⇒r=((a(b−x)+b(a−y)−(b−x)(a−y))/( (√(a^2 +x^2 ))+(√(b^2 +y^2 ))+(√((b−x)^2 +(a−y)^2 )))) (a−r_a )x−r_a a=r_a (√(a^2 +x^2 )) ⇒x=((2r_a (a−r_a ))/(a−2r_a ))=2(((α−1)/(α−2)))r_a similarly ⇒y=((2r_b (b−r_b ))/(b−2r_b ))=2(((β−1)/(β−2)))r_b with α=(a/r_a ), β=(b/r_b ) ab−r_c (a+b)−(a−r_c )x−(b−r_c )y+xy=r_c (√((b−x)^2 +(a−y)^2 )) [ab−r_c (a+b)−(a−r_c )x−(b−r_c )y+xy]^2 =r_c ^2 [(b−x)^2 +(a−y)^2 ] [αβr_a r_b −r_c (αr_a +βr_b )−(αr_a −r_c )x−(βr_b −r_c )y+xy]^2 =r_c ^2 [(βr_b −x)^2 +(αr_a −y)^2 ] ⇒[r_a r_b αβ−r_c (r_a α+r_b β)−2r_a (r_a α−r_c )(((α−1)/(α−2)))−2r_b (r_b β−r_c )(((β−1)/(β−2)))+4r_a r_b (((α−1)/(α−2)))(((β−1)/(β−2)))]^2 =r_c ^2 {[r_b β−2r_a (((α−1)/(α−2)))]^2 +[r_a α−2r_b (((β−1)/(β−2)))]^2 } ⇒r=((r_a r_b [αβ+4(((α−1)/(α−2)))(((β−1)/(β−2)))])/(r_a (√(α^2 +4(((α−1)/(α−2)))^2 ))+r_b (√(β^2 +4(((β−1)/(β−2)))^2 ))+(√([r_b β−2(((α−1)/(α−2)))r_a ]^2 +[r_a α−2(((β−1)/(β−2)))r_b ]^2 ))))
$${an}\:{attempt}… \\ $$$${ax}={r}_{{a}} \left({a}+{x}+\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }\right) \\ $$$${by}={r}_{{b}} \left({b}+{y}+\sqrt{{b}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right) \\ $$$$\left({b}−{x}\right)\left({a}−{y}\right)={r}_{{c}} \left[\left({b}−{x}\right)+\left({a}−{y}\right)+\sqrt{\left({b}−{x}\right)^{\mathrm{2}} +\left({a}−{y}\right)^{\mathrm{2}} }\right] \\ $$$$ \\ $$$$\mathrm{2}{ab}−{ax}−{by}−\left({b}−{x}\right)\left({a}−{y}\right)={r}\left[\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }+\sqrt{{b}^{\mathrm{2}} +{y}^{\mathrm{2}} }+\sqrt{\left({b}−{x}\right)^{\mathrm{2}} +\left({a}−{y}\right)^{\mathrm{2}} }\right] \\ $$$$\Rightarrow{r}=\frac{{a}\left({b}−{x}\right)+{b}\left({a}−{y}\right)−\left({b}−{x}\right)\left({a}−{y}\right)}{\:\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }+\sqrt{{b}^{\mathrm{2}} +{y}^{\mathrm{2}} }+\sqrt{\left({b}−{x}\right)^{\mathrm{2}} +\left({a}−{y}\right)^{\mathrm{2}} }} \\ $$$$ \\ $$$$\left({a}−{r}_{{a}} \right){x}−{r}_{{a}} {a}={r}_{{a}} \sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}{r}_{{a}} \left({a}−{r}_{{a}} \right)}{{a}−\mathrm{2}{r}_{{a}} }=\mathrm{2}\left(\frac{\alpha−\mathrm{1}}{\alpha−\mathrm{2}}\right){r}_{{a}} \\ $$$${similarly} \\ $$$$\Rightarrow{y}=\frac{\mathrm{2}{r}_{{b}} \left({b}−{r}_{{b}} \right)}{{b}−\mathrm{2}{r}_{{b}} }=\mathrm{2}\left(\frac{\beta−\mathrm{1}}{\beta−\mathrm{2}}\right){r}_{{b}} \\ $$$${with}\:\alpha=\frac{{a}}{{r}_{{a}} },\:\beta=\frac{{b}}{{r}_{{b}} } \\ $$$${ab}−{r}_{{c}} \left({a}+{b}\right)−\left({a}−{r}_{{c}} \right){x}−\left({b}−{r}_{{c}} \right){y}+{xy}={r}_{{c}} \sqrt{\left({b}−{x}\right)^{\mathrm{2}} +\left({a}−{y}\right)^{\mathrm{2}} } \\ $$$$\left[{ab}−{r}_{{c}} \left({a}+{b}\right)−\left({a}−{r}_{{c}} \right){x}−\left({b}−{r}_{{c}} \right){y}+{xy}\right]^{\mathrm{2}} ={r}_{{c}} ^{\mathrm{2}} \left[\left({b}−{x}\right)^{\mathrm{2}} +\left({a}−{y}\right)^{\mathrm{2}} \right] \\ $$$$\left[\alpha\beta{r}_{{a}} {r}_{{b}} −{r}_{{c}} \left(\alpha{r}_{{a}} +\beta{r}_{{b}} \right)−\left(\alpha{r}_{{a}} −{r}_{{c}} \right){x}−\left(\beta{r}_{{b}} −{r}_{{c}} \right){y}+{xy}\right]^{\mathrm{2}} ={r}_{{c}} ^{\mathrm{2}} \left[\left(\beta{r}_{{b}} −{x}\right)^{\mathrm{2}} +\left(\alpha{r}_{{a}} −{y}\right)^{\mathrm{2}} \right] \\ $$$$\Rightarrow\left[{r}_{{a}} {r}_{{b}} \alpha\beta−{r}_{{c}} \left({r}_{{a}} \alpha+{r}_{{b}} \beta\right)−\mathrm{2}{r}_{{a}} \left({r}_{{a}} \alpha−{r}_{{c}} \right)\left(\frac{\alpha−\mathrm{1}}{\alpha−\mathrm{2}}\right)−\mathrm{2}{r}_{{b}} \left({r}_{{b}} \beta−{r}_{{c}} \right)\left(\frac{\beta−\mathrm{1}}{\beta−\mathrm{2}}\right)+\mathrm{4}{r}_{{a}} {r}_{{b}} \left(\frac{\alpha−\mathrm{1}}{\alpha−\mathrm{2}}\right)\left(\frac{\beta−\mathrm{1}}{\beta−\mathrm{2}}\right)\right]^{\mathrm{2}} ={r}_{{c}} ^{\mathrm{2}} \left\{\left[{r}_{{b}} \beta−\mathrm{2}{r}_{{a}} \left(\frac{\alpha−\mathrm{1}}{\alpha−\mathrm{2}}\right)\right]^{\mathrm{2}} +\left[{r}_{{a}} \alpha−\mathrm{2}{r}_{{b}} \left(\frac{\beta−\mathrm{1}}{\beta−\mathrm{2}}\right)\right]^{\mathrm{2}} \right\} \\ $$$$\Rightarrow{r}=\frac{{r}_{{a}} {r}_{{b}} \left[\alpha\beta+\mathrm{4}\left(\frac{\alpha−\mathrm{1}}{\alpha−\mathrm{2}}\right)\left(\frac{\beta−\mathrm{1}}{\beta−\mathrm{2}}\right)\right]}{{r}_{{a}} \sqrt{\alpha^{\mathrm{2}} +\mathrm{4}\left(\frac{\alpha−\mathrm{1}}{\alpha−\mathrm{2}}\right)^{\mathrm{2}} }+{r}_{{b}} \sqrt{\beta^{\mathrm{2}} +\mathrm{4}\left(\frac{\beta−\mathrm{1}}{\beta−\mathrm{2}}\right)^{\mathrm{2}} }+\sqrt{\left[{r}_{{b}} \beta−\mathrm{2}\left(\frac{\alpha−\mathrm{1}}{\alpha−\mathrm{2}}\right){r}_{{a}} \right]^{\mathrm{2}} +\left[{r}_{{a}} \alpha−\mathrm{2}\left(\frac{\beta−\mathrm{1}}{\beta−\mathrm{2}}\right){r}_{{b}} \right]^{\mathrm{2}} }} \\ $$
Commented by mr W last updated on 22/Jan/20
it seems that the fourth circle is not unique when the three circls are given.
$${it}\:{seems}\:{that}\:{the}\:{fourth}\:{circle}\:{is}\:{not} \\ $$$${unique}\:{when}\:{the}\:{three}\:{circls}\:{are}\:{given}. \\ $$
Commented by behi83417@gmail.com last updated on 23/Jan/20
r_b =(s_b /p_b )=((by)/(b+y+(√(b^2 +y^2 ))))⇒ by=(b+y+(√(b^2 +y^2 )))r_b ⇒(b−r_b )y−br_b =(√(b^2 +y^2 )).r_b ⇒(b−r_b )^2 y^2 −2br_b (b−r_b )y+b^2 r_b ^2 =(b^2 +y^2 )r_b ^2 ⇒b^2 y^2 −2y^2 br_b +y^2 r_b ^2 −2yb^2 r_b +2ybr_b ^2 +b^2 r_b ^2 =b^2 r_b ^2 +y^2 r_b ^2 ⇒b^2 y^2 −2y^2 br_b −2yb^2 r_b +2ybr_b ^2 =0 ⇒ { ((y=0)),((y(b^2 −2br_b )−2b^2 r_b +2br_b ^2 =0)) :} ⇒y=((2br_b (b−r_b ))/(b(b−2r_b )))=2r_b .(((b−r_b )/(b−2r_b ))) ⇒x=2r_a .(((a−r_a )/(a−2r_a ))) −−−−−−−−−−−−−−−−−−
$$\mathrm{r}_{\mathrm{b}} =\frac{\mathrm{s}_{\mathrm{b}} }{\mathrm{p}_{\mathrm{b}} }=\frac{\mathrm{by}}{\mathrm{b}+\mathrm{y}+\sqrt{\mathrm{b}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }}\Rightarrow \\ $$$$\mathrm{by}=\left(\mathrm{b}+\mathrm{y}+\sqrt{\mathrm{b}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\right)\mathrm{r}_{\mathrm{b}} \Rightarrow\left(\mathrm{b}−\mathrm{r}_{\mathrm{b}} \right)\mathrm{y}−\mathrm{br}_{\mathrm{b}} =\sqrt{\mathrm{b}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }.\mathrm{r}_{\mathrm{b}} \\ $$$$\Rightarrow\left(\mathrm{b}−\mathrm{r}_{\mathrm{b}} \right)^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} −\mathrm{2br}_{\mathrm{b}} \left(\mathrm{b}−\mathrm{r}_{\mathrm{b}} \right)\mathrm{y}+\mathrm{b}^{\mathrm{2}} \mathrm{r}_{\mathrm{b}} ^{\mathrm{2}} =\left(\mathrm{b}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)\mathrm{r}_{\mathrm{b}} ^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{b}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} −\mathrm{2y}^{\mathrm{2}} \mathrm{br}_{\mathrm{b}} +\mathrm{y}^{\mathrm{2}} \mathrm{r}_{\mathrm{b}} ^{\mathrm{2}} −\mathrm{2yb}^{\mathrm{2}} \mathrm{r}_{\mathrm{b}} +\mathrm{2ybr}_{\mathrm{b}} ^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \mathrm{r}_{\mathrm{b}} ^{\mathrm{2}} =\mathrm{b}^{\mathrm{2}} \mathrm{r}_{\mathrm{b}} ^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \mathrm{r}_{\mathrm{b}} ^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{b}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} −\mathrm{2y}^{\mathrm{2}} \mathrm{br}_{\mathrm{b}} −\mathrm{2yb}^{\mathrm{2}} \mathrm{r}_{\mathrm{b}} +\mathrm{2ybr}_{\mathrm{b}} ^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\begin{cases}{\mathrm{y}=\mathrm{0}}\\{\mathrm{y}\left(\mathrm{b}^{\mathrm{2}} −\mathrm{2br}_{\mathrm{b}} \right)−\mathrm{2b}^{\mathrm{2}} \mathrm{r}_{\mathrm{b}} +\mathrm{2br}_{\mathrm{b}} ^{\mathrm{2}} =\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{2br}_{\mathrm{b}} \left(\mathrm{b}−\mathrm{r}_{\mathrm{b}} \right)}{\mathrm{b}\left(\mathrm{b}−\mathrm{2r}_{\mathrm{b}} \right)}=\mathrm{2r}_{\mathrm{b}} .\left(\frac{\mathrm{b}−\mathrm{r}_{\mathrm{b}} }{\mathrm{b}−\mathrm{2r}_{\mathrm{b}} }\right) \\ $$$$\Rightarrow\mathrm{x}=\mathrm{2r}_{\mathrm{a}} .\left(\frac{\mathrm{a}−\mathrm{r}_{\mathrm{a}} }{\mathrm{a}−\mathrm{2r}_{\mathrm{a}} }\right) \\ $$$$−−−−−−−−−−−−−−−−−− \\ $$
Commented by mr W last updated on 23/Jan/20
so far so good. thanks sir!
$${so}\:{far}\:{so}\:{good}.\:{thanks}\:{sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *