Menu Close

Question-79254

Tinku Tara 0 Comments
Pin




Question Number 79254 by mr W last updated on 23/Jan/20
Commented by mr W last updated on 23/Jan/20
If the side length of the square is 10, find 1) the radius of the smallest circle 2) the shaded area
$${If}\:{the}\:{side}\:{length}\:{of}\:{the}\:{square}\:{is}\:\mathrm{10}, \\ $$$${find} \\ $$$$\left.\mathrm{1}\right)\:{the}\:{radius}\:{of}\:{the}\:{smallest}\:{circle} \\ $$$$\left.\mathrm{2}\right)\:{the}\:{shaded}\:{area} \\ $$
Commented by key of knowledge last updated on 23/Jan/20
1)r=(5/3) 2)i think need (∫) !
$$\left.\mathrm{1}\left.\right)\mathrm{r}=\frac{\mathrm{5}}{\mathrm{3}}\:\:\:\:\:\:\:\:\:\mathrm{2}\right)\mathrm{i}\:\mathrm{think}\:\mathrm{need}\:\left(\int\right)\:! \\ $$
Answered by john santu last updated on 24/Jan/20
Commented by mr W last updated on 24/Jan/20
not correct sir! it seems but it is not: AP not⊥PB, AP≠5.
$${not}\:{correct}\:{sir}! \\ $$$${it}\:{seems}\:{but}\:{it}\:{is}\:{not}:\:{AP}\:{not}\bot{PB},\:{AP}\neq\mathrm{5}. \\ $$
Commented by john santu last updated on 24/Jan/20
r_A + r = 5... (i) (r_A +5)^2 =25+(10−r_A )^2 r_A ^2 +10r_A +25=25+100−20r_A +r_A ^2 30r_A = 100 ⇒r_A =((10)/3) now we work (i) r = 5 −((10)/3)=(5/3)
$${r}_{{A}} +\:{r}\:=\:\mathrm{5}…\:\left({i}\right) \\ $$$$\left({r}_{{A}} +\mathrm{5}\right)^{\mathrm{2}} =\mathrm{25}+\left(\mathrm{10}−{r}_{{A}} \right)^{\mathrm{2}} \\ $$$${r}_{{A}} ^{\mathrm{2}} +\mathrm{10}{r}_{{A}} +\mathrm{25}=\mathrm{25}+\mathrm{100}−\mathrm{20}{r}_{{A}} +{r}_{{A}} ^{\mathrm{2}} \\ $$$$\mathrm{30}{r}_{{A}} \:=\:\mathrm{100}\:\Rightarrow{r}_{{A}} =\frac{\mathrm{10}}{\mathrm{3}} \\ $$$${now}\:{we}\:{work}\:\left({i}\right)\:{r}\:=\:\mathrm{5}\:−\frac{\mathrm{10}}{\mathrm{3}}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$ \\ $$
Commented by john santu last updated on 24/Jan/20
prove it if it′s not right mister
$${prove}\:{it}\:{if}\:{it}'{s}\:{not}\:{right}\:{mister} \\ $$
Commented by mr W last updated on 24/Jan/20
sir: what i meant above is it seems but it is not proved: AP ⊥PB, AP=5. you just assumed these are true. in fact i can′t see in your solution that you utilised the condition that the smallest circle also tangents the largest quartocircle. i have not calculated this question, so i have no result yet. maybe your result is regardless correct. then it′s by accident, i think. i′ll post my solution and compare.
$${sir}:\:{what}\:{i}\:{meant}\:{above}\:{is} \\ $$$${it}\:{seems}\:{but}\:{it}\:{is}\:{not}\:{proved}:\:{AP}\:\bot{PB},\:{AP}=\mathrm{5}. \\ $$$${you}\:{just}\:{assumed}\:{these}\:{are}\:{true}. \\ $$$${in}\:{fact}\:{i}\:{can}'{t}\:{see}\:{in}\:{your}\:{solution} \\ $$$${that}\:{you}\:{utilised}\:{the}\:{condition}\:{that} \\ $$$${the}\:{smallest}\:{circle}\:{also}\:{tangents}\:{the} \\ $$$${largest}\:{quartocircle}. \\ $$$${i}\:{have}\:{not}\:{calculated}\:{this}\:{question}, \\ $$$${so}\:{i}\:{have}\:{no}\:{result}\:{yet}.\:{maybe}\:{your} \\ $$$${result}\:{is}\:{regardless}\:{correct}.\:{then} \\ $$$${it}'{s}\:{by}\:{accident},\:{i}\:{think}. \\ $$$${i}'{ll}\:{post}\:{my}\:{solution}\:{and}\:{compare}. \\ $$
Commented by mr W last updated on 24/Jan/20
i have calculated. your result (values) is correct.
$${i}\:{have}\:{calculated}.\:{your}\:{result}\:\left({values}\right) \\ $$$${is}\:{correct}. \\ $$
Answered by mr W last updated on 24/Jan/20
Commented by mr W last updated on 24/Jan/20
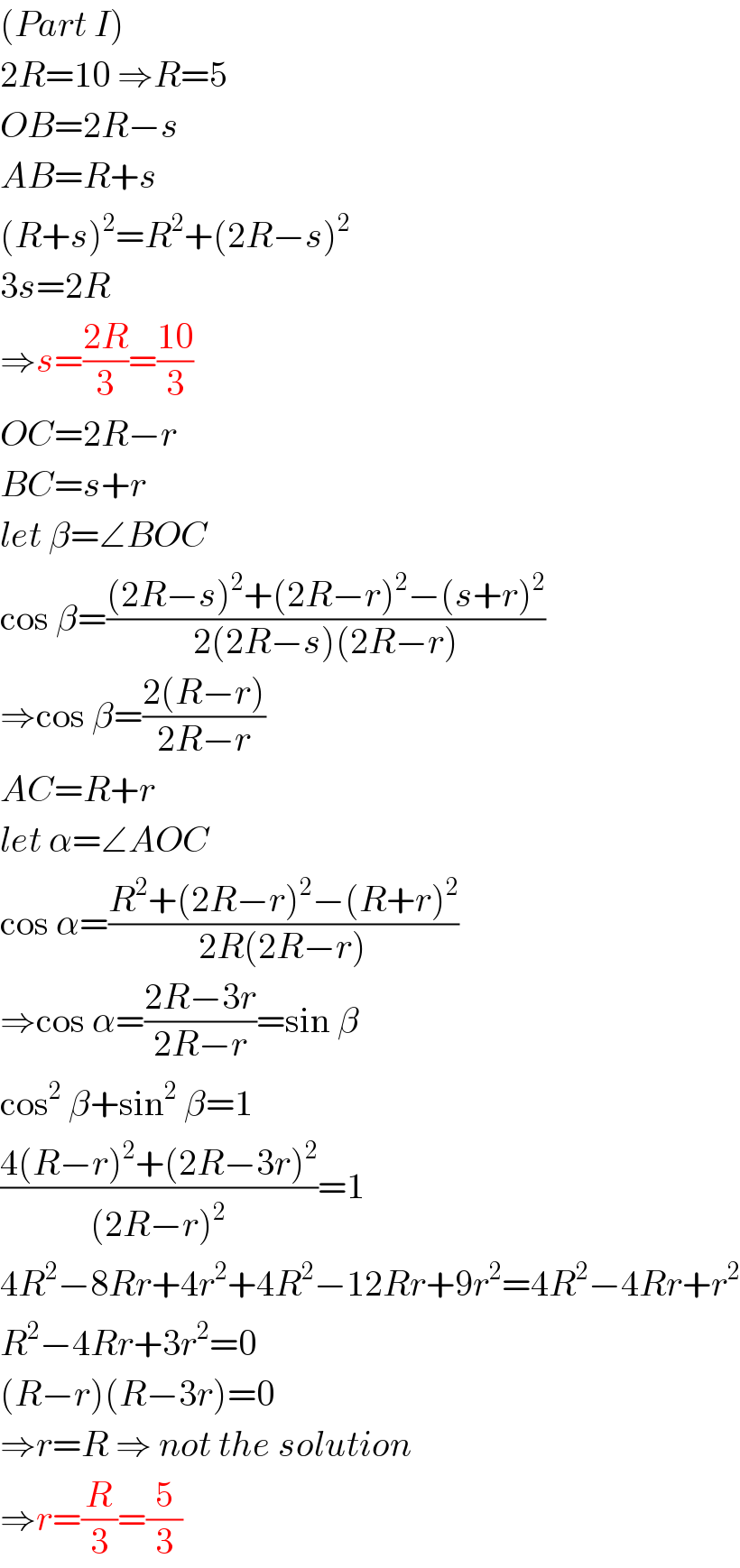
(Part I) 2R=10 ⇒R=5 OB=2R−s AB=R+s (R+s)^2 =R^2 +(2R−s)^2 3s=2R ⇒s=((2R)/3)=((10)/3) OC=2R−r BC=s+r let β=∠BOC cos β=(((2R−s)^2 +(2R−r)^2 −(s+r)^2 )/(2(2R−s)(2R−r))) ⇒cos β=((2(R−r))/(2R−r)) AC=R+r let α=∠AOC cos α=((R^2 +(2R−r)^2 −(R+r)^2 )/(2R(2R−r))) ⇒cos α=((2R−3r)/(2R−r))=sin β cos^2 β+sin^2 β=1 ((4(R−r)^2 +(2R−3r)^2 )/((2R−r)^2 ))=1 4R^2 −8Rr+4r^2 +4R^2 −12Rr+9r^2 =4R^2 −4Rr+r^2 R^2 −4Rr+3r^2 =0 (R−r)(R−3r)=0 ⇒r=R ⇒ not the solution ⇒r=(R/3)=(5/3)
$$\left({Part}\:{I}\right) \\ $$$$\mathrm{2}{R}=\mathrm{10}\:\Rightarrow{R}=\mathrm{5} \\ $$$${OB}=\mathrm{2}{R}−{s} \\ $$$${AB}={R}+{s} \\ $$$$\left({R}+{s}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} +\left(\mathrm{2}{R}−{s}\right)^{\mathrm{2}} \\ $$$$\mathrm{3}{s}=\mathrm{2}{R} \\ $$$$\Rightarrow{s}=\frac{\mathrm{2}{R}}{\mathrm{3}}=\frac{\mathrm{10}}{\mathrm{3}} \\ $$$${OC}=\mathrm{2}{R}−{r} \\ $$$${BC}={s}+{r} \\ $$$${let}\:\beta=\angle{BOC} \\ $$$$\mathrm{cos}\:\beta=\frac{\left(\mathrm{2}{R}−{s}\right)^{\mathrm{2}} +\left(\mathrm{2}{R}−{r}\right)^{\mathrm{2}} −\left({s}+{r}\right)^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{2}{R}−{s}\right)\left(\mathrm{2}{R}−{r}\right)} \\ $$$$\Rightarrow\mathrm{cos}\:\beta=\frac{\mathrm{2}\left({R}−{r}\right)}{\mathrm{2}{R}−{r}} \\ $$$${AC}={R}+{r} \\ $$$${let}\:\alpha=\angle{AOC} \\ $$$$\mathrm{cos}\:\alpha=\frac{{R}^{\mathrm{2}} +\left(\mathrm{2}{R}−{r}\right)^{\mathrm{2}} −\left({R}+{r}\right)^{\mathrm{2}} }{\mathrm{2}{R}\left(\mathrm{2}{R}−{r}\right)} \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\frac{\mathrm{2}{R}−\mathrm{3}{r}}{\mathrm{2}{R}−{r}}=\mathrm{sin}\:\beta \\ $$$$\mathrm{cos}^{\mathrm{2}} \:\beta+\mathrm{sin}^{\mathrm{2}} \:\beta=\mathrm{1} \\ $$$$\frac{\mathrm{4}\left({R}−{r}\right)^{\mathrm{2}} +\left(\mathrm{2}{R}−\mathrm{3}{r}\right)^{\mathrm{2}} }{\left(\mathrm{2}{R}−{r}\right)^{\mathrm{2}} }=\mathrm{1} \\ $$$$\mathrm{4}{R}^{\mathrm{2}} −\mathrm{8}{Rr}+\mathrm{4}{r}^{\mathrm{2}} +\mathrm{4}{R}^{\mathrm{2}} −\mathrm{12}{Rr}+\mathrm{9}{r}^{\mathrm{2}} =\mathrm{4}{R}^{\mathrm{2}} −\mathrm{4}{Rr}+{r}^{\mathrm{2}} \\ $$$${R}^{\mathrm{2}} −\mathrm{4}{Rr}+\mathrm{3}{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({R}−{r}\right)\left({R}−\mathrm{3}{r}\right)=\mathrm{0} \\ $$$$\Rightarrow{r}={R}\:\Rightarrow\:{not}\:{the}\:{solution} \\ $$$$\Rightarrow{r}=\frac{{R}}{\mathrm{3}}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$
Commented by john santu last updated on 24/Jan/20
(10−r)^2 =5^2 +(5+r)^2 100−20r+r^2 =25+25+10r+r^2 50 = 30r ⇒r= (5/3)
$$\left(\mathrm{10}−{r}\right)^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} +\left(\mathrm{5}+{r}\right)^{\mathrm{2}} \\ $$$$\mathrm{100}−\mathrm{20}{r}+{r}^{\mathrm{2}} =\mathrm{25}+\mathrm{25}+\mathrm{10}{r}+{r}^{\mathrm{2}} \\ $$$$\mathrm{50}\:=\:\mathrm{30}{r}\:\Rightarrow{r}=\:\frac{\mathrm{5}}{\mathrm{3}} \\ $$
Commented by mr W last updated on 24/Jan/20
(10−r)^2 =5^2 +(5+r)^2 means OA⊥AC, but i think this is not yet proved. or how did you get that OA⊥AC?
$$\left(\mathrm{10}−{r}\right)^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} +\left(\mathrm{5}+{r}\right)^{\mathrm{2}} \:{means}\:{OA}\bot{AC}, \\ $$$${but}\:{i}\:{think}\:{this}\:{is}\:{not}\:{yet}\:{proved}.\:{or} \\ $$$${how}\:{did}\:{you}\:{get}\:{that}\:{OA}\bot{AC}? \\ $$
Commented by john santu last updated on 24/Jan/20
mister. we cannot claim our way is right,so we deem different ways wrong . it is shortsighted. everyone′s point of view is different
$${mister}.\:{we}\:{cannot}\:{claim}\:{our} \\ $$$${way}\:{is}\:{right},{so}\:{we}\:{deem}\:{different} \\ $$$${ways}\:{wrong}\:.\:{it}\:{is}\:{shortsighted}. \\ $$$${everyone}'{s}\:{point}\:{of}\:{view}\:{is} \\ $$$${different} \\ $$
Commented by john santu last updated on 24/Jan/20
Commented by john santu last updated on 24/Jan/20
look sir
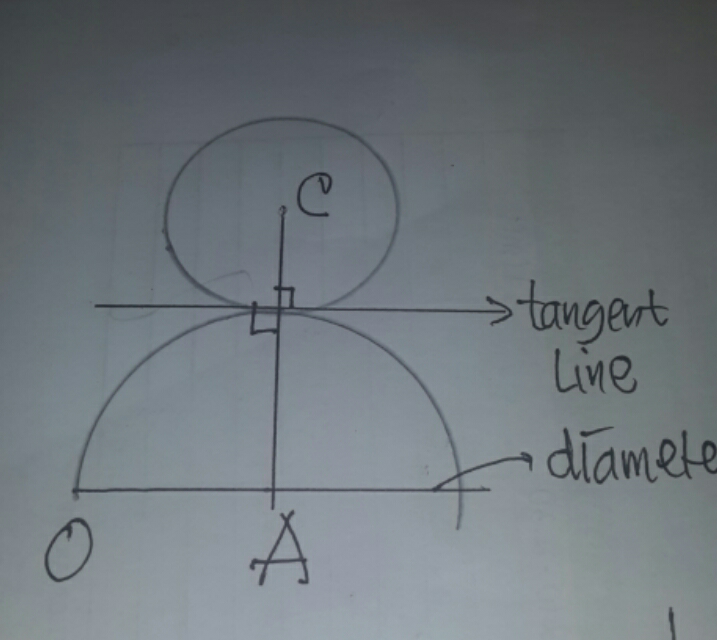
$${look}\:{sir} \\ $$
Commented by mr W last updated on 24/Jan/20
discussion is always good. btw your diagram didn′t answer my question how to get that OA⊥AC. it says only that AC⊥the tangent line.
$${discussion}\:{is}\:{always}\:{good}. \\ $$$${btw}\:{your}\:{diagram}\:{didn}'{t}\:{answer}\:{my}\: \\ $$$${question}\:{how}\:{to}\:{get}\:{that}\:{OA}\bot{AC}.\:{it} \\ $$$${says}\:{only}\:{that}\:{AC}\bot{the}\:{tangent}\:{line}. \\ $$
Answered by mr W last updated on 24/Jan/20
Commented by mr W last updated on 24/Jan/20
(Part II) as calculated in part I we have got s=((2R)/3)=((10)/3) r=(R/3)=(5/3) BC=s+r=((2R)/3)+(R/3)=R=OA OB=2R−s=2R−((2R)/3)=((4R)/3) AC=R+r=R+(R/3)=((4R)/3)=OB ⇒OACB is rectangle. tan β=(R/((4R)/3))=(3/4) ⇒β=tan^(−1) (3/4) γ=(π/2)+β A_(ODE^(⌢) ) =((β(2R)^2 )/2)=2R^2 β A_(ΔOBC) =(1/2)×R×((4R)/3)=((2R^2 )/3) A_(BDF^(⌢) ) =(π/4)(((2R)/3))^2 =((πR^2 )/9) A_(FCE^(⌢) ) =(γ/2)((R/3))^2 =(R^2 /(18))((π/2)+β) A_(shaded) =A_(ODE^(⌢) ) −A_(ΔOBC) −A_(BDF^(⌢) ) −A_(FCE^(⌢) ) =2R^2 β−((2R^2 )/3)−((πR^2 )/9)−(R^2 /(18))((π/2)+β) =(((70β−5π−24)R^2 )/(36)) ⇒A_(shaded) =(((70 tan^(−1) (3/4)−5π−24)R^2 )/(36))≈0.148253R^2 ≈3.706329
$$\left({Part}\:{II}\right) \\ $$$${as}\:{calculated}\:{in}\:{part}\:{I}\:{we}\:{have}\:{got} \\ $$$${s}=\frac{\mathrm{2}{R}}{\mathrm{3}}=\frac{\mathrm{10}}{\mathrm{3}} \\ $$$${r}=\frac{{R}}{\mathrm{3}}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$${BC}={s}+{r}=\frac{\mathrm{2}{R}}{\mathrm{3}}+\frac{{R}}{\mathrm{3}}={R}={OA} \\ $$$${OB}=\mathrm{2}{R}−{s}=\mathrm{2}{R}−\frac{\mathrm{2}{R}}{\mathrm{3}}=\frac{\mathrm{4}{R}}{\mathrm{3}} \\ $$$${AC}={R}+{r}={R}+\frac{{R}}{\mathrm{3}}=\frac{\mathrm{4}{R}}{\mathrm{3}}={OB} \\ $$$$\Rightarrow{OACB}\:{is}\:{rectangle}. \\ $$$$\mathrm{tan}\:\beta=\frac{{R}}{\frac{\mathrm{4}{R}}{\mathrm{3}}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\beta=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\gamma=\frac{\pi}{\mathrm{2}}+\beta \\ $$$${A}_{\overset{\frown} {{ODE}}} =\frac{\beta\left(\mathrm{2}{R}\right)^{\mathrm{2}} }{\mathrm{2}}=\mathrm{2}{R}^{\mathrm{2}} \beta \\ $$$${A}_{\Delta{OBC}} =\frac{\mathrm{1}}{\mathrm{2}}×{R}×\frac{\mathrm{4}{R}}{\mathrm{3}}=\frac{\mathrm{2}{R}^{\mathrm{2}} }{\mathrm{3}} \\ $$$${A}_{\overset{\frown} {{BDF}}} =\frac{\pi}{\mathrm{4}}\left(\frac{\mathrm{2}{R}}{\mathrm{3}}\right)^{\mathrm{2}} =\frac{\pi{R}^{\mathrm{2}} }{\mathrm{9}} \\ $$$${A}_{\overset{\frown} {{FCE}}} =\frac{\gamma}{\mathrm{2}}\left(\frac{{R}}{\mathrm{3}}\right)^{\mathrm{2}} =\frac{{R}^{\mathrm{2}} }{\mathrm{18}}\left(\frac{\pi}{\mathrm{2}}+\beta\right) \\ $$$${A}_{{shaded}} ={A}_{\overset{\frown} {{ODE}}} −{A}_{\Delta{OBC}} −{A}_{\overset{\frown} {{BDF}}} −{A}_{\overset{\frown} {{FCE}}} \\ $$$$=\mathrm{2}{R}^{\mathrm{2}} \beta−\frac{\mathrm{2}{R}^{\mathrm{2}} }{\mathrm{3}}−\frac{\pi{R}^{\mathrm{2}} }{\mathrm{9}}−\frac{{R}^{\mathrm{2}} }{\mathrm{18}}\left(\frac{\pi}{\mathrm{2}}+\beta\right) \\ $$$$=\frac{\left(\mathrm{70}\beta−\mathrm{5}\pi−\mathrm{24}\right){R}^{\mathrm{2}} }{\mathrm{36}} \\ $$$$\Rightarrow{A}_{{shaded}} =\frac{\left(\mathrm{70}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}}−\mathrm{5}\pi−\mathrm{24}\right){R}^{\mathrm{2}} }{\mathrm{36}}\approx\mathrm{0}.\mathrm{148253}{R}^{\mathrm{2}} \\ $$$$\approx\mathrm{3}.\mathrm{706329} \\ $$
Answered by mr W last updated on 24/Jan/20
Commented by mr W last updated on 24/Jan/20
here is an other way to solve using the Descartes′ theorem (see Q77681 for more details) R_1 =2R=10 R_2 =R=5 R_3 =s=? R_4 =r=? applying Descartes′ theorem on R_1 ,2×R_2 and R_3 : (−(1/R_1 )+(2/R_2 )+(1/R_3 ))^2 =2((1/R_1 ^2 )+(2/R_2 ^2 )+(1/R_3 ^2 )) (−(1/(2R))+(2/R)+(1/s))^2 =2((1/(4R^2 ))+(2/R^2 )+(1/s^2 )) 4(R^2 /s^2 )−12(R/s)+9=0 (2(R/s)−3)^2 =0 ⇒s=((2R)/3)=((10)/3) applying Descartes′ theorem on R_1 ,R_2 ,R_3 and R_4 : (−(1/R_1 )+(1/R_2 )+(1/R_3 )+(1/R_4 ))^2 =2((1/R_1 ^2 )+(1/R_2 ^2 )+(1/R_3 ^2 )+(1/R_4 ^2 )) (−(1/(2R))+(1/R)+(3/(2R))+(1/r))^2 =2((1/(4R^2 ))+(1/R^2 )+(9/(4R^2 ))+(1/r^2 )) (R^2 /r^2 )−4(R/r)+3=0 ((R/r)−1)((R/r)−3)=0 ⇒r=R ⇒not the searched circle ⇒r=(R/3)=(5/3)
$${here}\:{is}\:{an}\:{other}\:{way}\:{to}\:{solve}\:{using} \\ $$$${the}\:{Descartes}'\:{theorem} \\ $$$$\left({see}\:{Q}\mathrm{77681}\:{for}\:{more}\:{details}\right) \\ $$$$ \\ $$$${R}_{\mathrm{1}} =\mathrm{2}{R}=\mathrm{10} \\ $$$${R}_{\mathrm{2}} ={R}=\mathrm{5} \\ $$$${R}_{\mathrm{3}} ={s}=? \\ $$$${R}_{\mathrm{4}} ={r}=? \\ $$$$ \\ $$$${applying}\:{Descartes}'\:{theorem}\:{on} \\ $$$${R}_{\mathrm{1}} ,\mathrm{2}×{R}_{\mathrm{2}} \:{and}\:{R}_{\mathrm{3}} : \\ $$$$\left(−\frac{\mathrm{1}}{{R}_{\mathrm{1}} }+\frac{\mathrm{2}}{{R}_{\mathrm{2}} }+\frac{\mathrm{1}}{{R}_{\mathrm{3}} }\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{1}}{{R}_{\mathrm{1}} ^{\mathrm{2}} }+\frac{\mathrm{2}}{{R}_{\mathrm{2}} ^{\mathrm{2}} }+\frac{\mathrm{1}}{{R}_{\mathrm{3}} ^{\mathrm{2}} }\right) \\ $$$$\left(−\frac{\mathrm{1}}{\mathrm{2}{R}}+\frac{\mathrm{2}}{{R}}+\frac{\mathrm{1}}{{s}}\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{4}{R}^{\mathrm{2}} }+\frac{\mathrm{2}}{{R}^{\mathrm{2}} }+\frac{\mathrm{1}}{{s}^{\mathrm{2}} }\right) \\ $$$$\mathrm{4}\frac{{R}^{\mathrm{2}} }{{s}^{\mathrm{2}} }−\mathrm{12}\frac{{R}}{{s}}+\mathrm{9}=\mathrm{0} \\ $$$$\left(\mathrm{2}\frac{{R}}{{s}}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{s}=\frac{\mathrm{2}{R}}{\mathrm{3}}=\frac{\mathrm{10}}{\mathrm{3}} \\ $$$$ \\ $$$${applying}\:{Descartes}'\:{theorem}\:{on} \\ $$$${R}_{\mathrm{1}} ,{R}_{\mathrm{2}} ,{R}_{\mathrm{3}} \:{and}\:{R}_{\mathrm{4}} : \\ $$$$\left(−\frac{\mathrm{1}}{{R}_{\mathrm{1}} }+\frac{\mathrm{1}}{{R}_{\mathrm{2}} }+\frac{\mathrm{1}}{{R}_{\mathrm{3}} }+\frac{\mathrm{1}}{{R}_{\mathrm{4}} }\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{1}}{{R}_{\mathrm{1}} ^{\mathrm{2}} }+\frac{\mathrm{1}}{{R}_{\mathrm{2}} ^{\mathrm{2}} }+\frac{\mathrm{1}}{{R}_{\mathrm{3}} ^{\mathrm{2}} }+\frac{\mathrm{1}}{{R}_{\mathrm{4}} ^{\mathrm{2}} }\right) \\ $$$$\left(−\frac{\mathrm{1}}{\mathrm{2}{R}}+\frac{\mathrm{1}}{{R}}+\frac{\mathrm{3}}{\mathrm{2}{R}}+\frac{\mathrm{1}}{{r}}\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{4}{R}^{\mathrm{2}} }+\frac{\mathrm{1}}{{R}^{\mathrm{2}} }+\frac{\mathrm{9}}{\mathrm{4}{R}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }\right) \\ $$$$\frac{{R}^{\mathrm{2}} }{{r}^{\mathrm{2}} }−\mathrm{4}\frac{{R}}{{r}}+\mathrm{3}=\mathrm{0} \\ $$$$\left(\frac{{R}}{{r}}−\mathrm{1}\right)\left(\frac{{R}}{{r}}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow{r}={R}\:\Rightarrow{not}\:{the}\:{searched}\:{circle} \\ $$$$\Rightarrow{r}=\frac{{R}}{\mathrm{3}}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *