Question Number 79309 by mr W last updated on 24/Jan/20
Commented by mr W last updated on 24/Jan/20

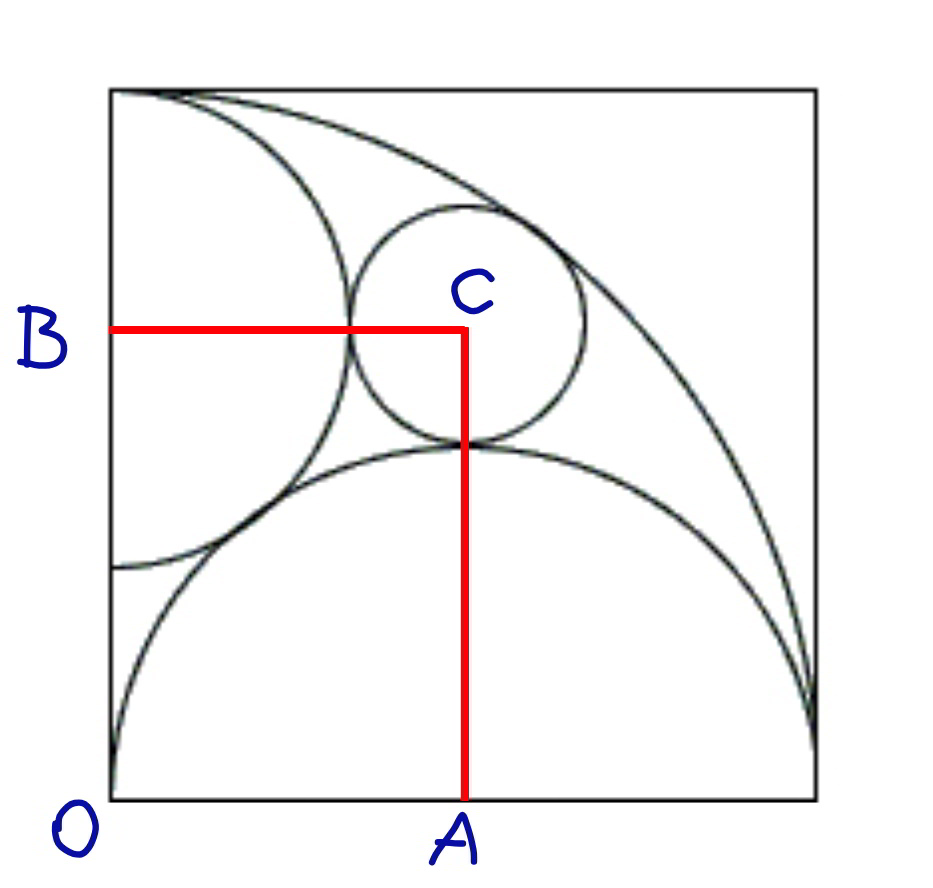
$${O},\:{A},\:{B},\:{C}\:{are}\:{the}\:{centers}\:{of}\:{the}\: \\ $$$${corresponding}\:{circles}. \\ $$$${prove}\:{that}\:{OACB}\:{is}\:{a}\:{rectangle}. \\ $$
Commented by john santu last updated on 24/Jan/20
$${i}\:{can}\:{prove}\:{by}\:{using}\:{vector} \\ $$
Commented by mr W last updated on 24/Jan/20

$${please}\:{post}\:{your}\:{solution},\:{thanks}\:{sir}! \\ $$$${i}\:{think}\:{there}\:{are}\:{many}\:{ways}\:{to}\:{prove}. \\ $$$${i}\:{posted}\:{this}\:{question}\:{to}\:{ask}\:{if}\:{there} \\ $$$${is}\:{an}\:{easy}\:{way}\:{to}\:{see}\:{that}\:{it}\:{is}\:{obviously} \\ $$$${a}\:{rectangle}. \\ $$
Answered by key of knowledge last updated on 24/Jan/20

$$\mathrm{get}\:\mathrm{ABCD}\:\mathrm{is}\:\mathrm{rectangle}.\mathrm{prove}\: \\ $$$$\mathrm{C}=\mathrm{center}\:\mathrm{of}\:\mathrm{circle}\:\left(\mathrm{sorry}.\mathrm{i}\:\mathrm{can}'\mathrm{t}\:\mathrm{rwite}\:\mathrm{good}\right) \\ $$
Commented by mr W last updated on 24/Jan/20
$${certainly}\:{this}\:{is}\:{a}\:{good}\:{way}\:{to}\:{prove}. \\ $$$${thanks}\:{sir}! \\ $$
