Question-79340

Question Number 79340 by TawaTawa last updated on 24/Jan/20

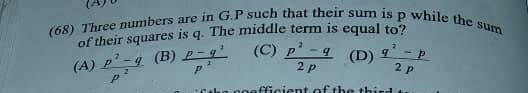
Commented by john santu last updated on 24/Jan/20

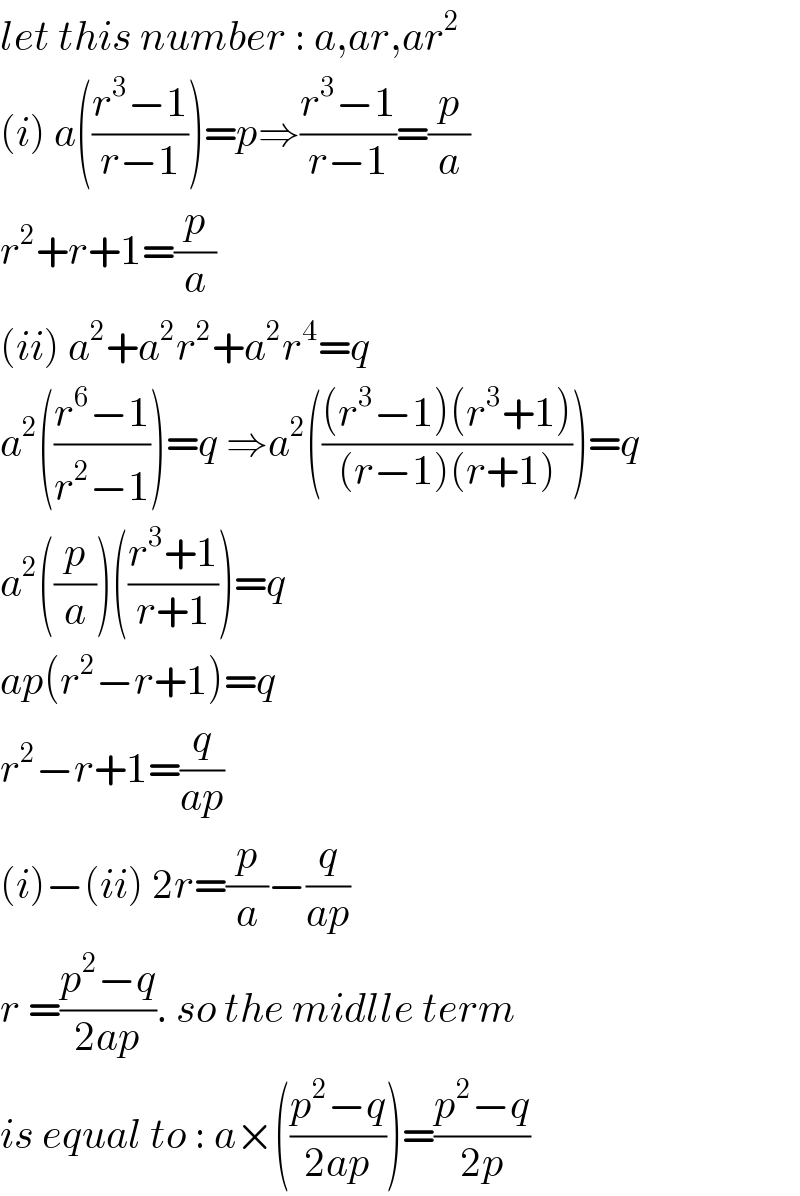
let this number : a,ar,ar^2 (i) a(((r^3 −1)/(r−1)))=p⇒((r^3 −1)/(r−1))=(p/a) r^2 +r+1=(p/a) (ii) a^2 +a^2 r^2 +a^2 r^4 =q a^2 (((r^6 −1)/(r^2 −1)))=q ⇒a^2 ((((r^3 −1)(r^3 +1))/((r−1)(r+1))))=q a^2 ((p/a))(((r^3 +1)/(r+1)))=q ap(r^2 −r+1)=q r^2 −r+1=(q/(ap)) (i)−(ii) 2r=(p/a)−(q/(ap)) r =((p^2 −q)/(2ap)). so the midlle term is equal to : a×(((p^2 −q)/(2ap)))=((p^2 −q)/(2p))

$${let}\:{this}\:{number}\::\:{a},{ar},{ar}^{\mathrm{2}} \\ $$$$\left({i}\right)\:{a}\left(\frac{{r}^{\mathrm{3}} −\mathrm{1}}{{r}−\mathrm{1}}\right)={p}\Rightarrow\frac{{r}^{\mathrm{3}} −\mathrm{1}}{{r}−\mathrm{1}}=\frac{{p}}{{a}} \\ $$$${r}^{\mathrm{2}} +{r}+\mathrm{1}=\frac{{p}}{{a}}\: \\ $$$$\left({ii}\right)\:{a}^{\mathrm{2}} +{a}^{\mathrm{2}} {r}^{\mathrm{2}} +{a}^{\mathrm{2}} {r}^{\mathrm{4}} ={q} \\ $$$${a}^{\mathrm{2}} \left(\frac{{r}^{\mathrm{6}} −\mathrm{1}}{{r}^{\mathrm{2}} −\mathrm{1}}\right)={q}\:\Rightarrow{a}^{\mathrm{2}} \left(\frac{\left({r}^{\mathrm{3}} −\mathrm{1}\right)\left({r}^{\mathrm{3}} +\mathrm{1}\right)}{\left({r}−\mathrm{1}\right)\left({r}+\mathrm{1}\right)}\right)={q} \\ $$$${a}^{\mathrm{2}} \left(\frac{{p}}{{a}}\right)\left(\frac{{r}^{\mathrm{3}} +\mathrm{1}}{{r}+\mathrm{1}}\right)={q} \\ $$$${ap}\left({r}^{\mathrm{2}} −{r}+\mathrm{1}\right)={q}\: \\ $$$${r}^{\mathrm{2}} −{r}+\mathrm{1}=\frac{{q}}{{ap}} \\ $$$$\left({i}\right)−\left({ii}\right)\:\mathrm{2}{r}=\frac{{p}}{{a}}−\frac{{q}}{{ap}} \\ $$$${r}\:=\frac{{p}^{\mathrm{2}} −{q}}{\mathrm{2}{ap}}.\:{so}\:{the}\:{midlle}\:{term} \\ $$$${is}\:{equal}\:{to}\::\:{a}×\left(\frac{{p}^{\mathrm{2}} −{q}}{\mathrm{2}{ap}}\right)=\frac{{p}^{\mathrm{2}} −{q}}{\mathrm{2}{p}} \\ $$

Commented by TawaTawa last updated on 24/Jan/20