Question-79359

Question Number 79359 by ahmadshahhimat775@gmail.com last updated on 24/Jan/20

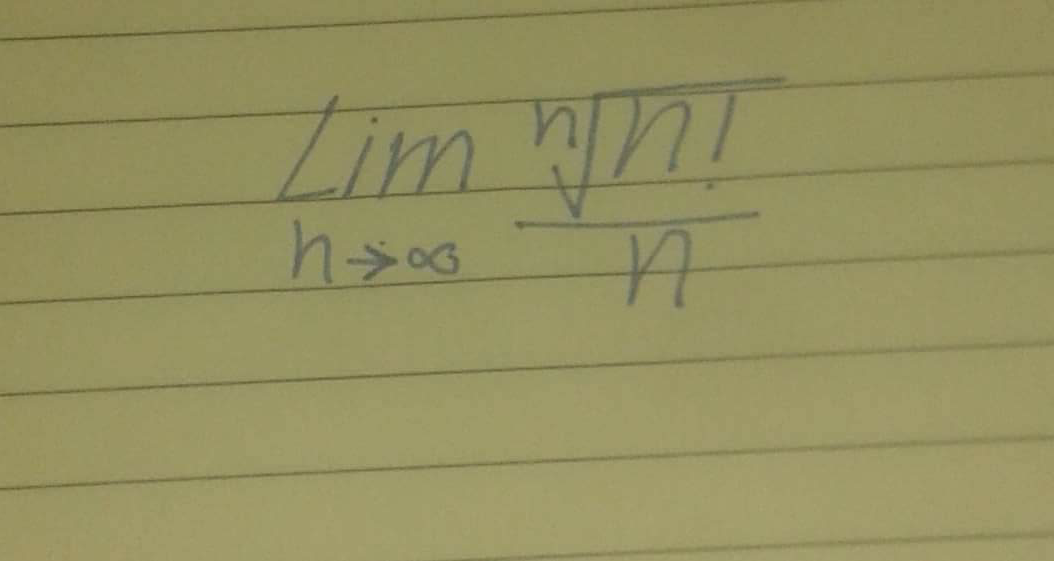
Commented by mathmax by abdo last updated on 24/Jan/20

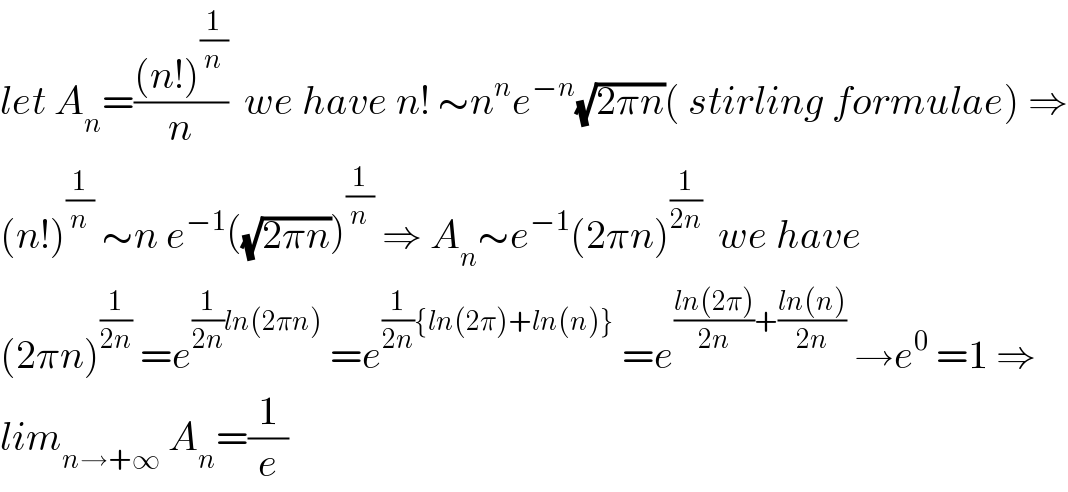
let A_n =(((n!)^(1/n) )/n) we have n! ∼n^n e^(−n) (√(2πn))( stirling formulae) ⇒ (n!)^(1/n) ∼n e^(−1) ((√(2πn)))^(1/n) ⇒ A_n ∼e^(−1) (2πn)^(1/(2n)) we have (2πn)^(1/(2n)) =e^((1/(2n))ln(2πn)) =e^((1/(2n)){ln(2π)+ln(n)}) =e^(((ln(2π))/(2n))+((ln(n))/(2n))) →e^0 =1 ⇒ lim_(n→+∞) A_n =(1/e)

$${let}\:{A}_{{n}} =\frac{\left({n}!\right)^{\frac{\mathrm{1}}{{n}}} }{{n}}\:\:{we}\:{have}\:{n}!\:\sim{n}^{{n}} {e}^{−{n}} \sqrt{\mathrm{2}\pi{n}}\left(\:{stirling}\:{formulae}\right)\:\Rightarrow \\ $$$$\left({n}!\right)^{\frac{\mathrm{1}}{{n}}} \:\sim{n}\:{e}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}\pi{n}}\right)^{\frac{\mathrm{1}}{{n}}} \:\Rightarrow\:{A}_{{n}} \sim{e}^{−\mathrm{1}} \left(\mathrm{2}\pi{n}\right)^{\frac{\mathrm{1}}{\mathrm{2}{n}}} \:\:{we}\:{have} \\ $$$$\left(\mathrm{2}\pi{n}\right)^{\frac{\mathrm{1}}{\mathrm{2}{n}}} \:={e}^{\frac{\mathrm{1}}{\mathrm{2}{n}}{ln}\left(\mathrm{2}\pi{n}\right)} \:={e}^{\frac{\mathrm{1}}{\mathrm{2}{n}}\left\{{ln}\left(\mathrm{2}\pi\right)+{ln}\left({n}\right)\right\}} \:={e}^{\frac{{ln}\left(\mathrm{2}\pi\right)}{\mathrm{2}{n}}+\frac{{ln}\left({n}\right)}{\mathrm{2}{n}}} \:\rightarrow{e}^{\mathrm{0}} \:=\mathrm{1}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} =\frac{\mathrm{1}}{{e}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply