Question Number 79361 by TawaTawa last updated on 24/Jan/20
Commented by mr W last updated on 24/Jan/20

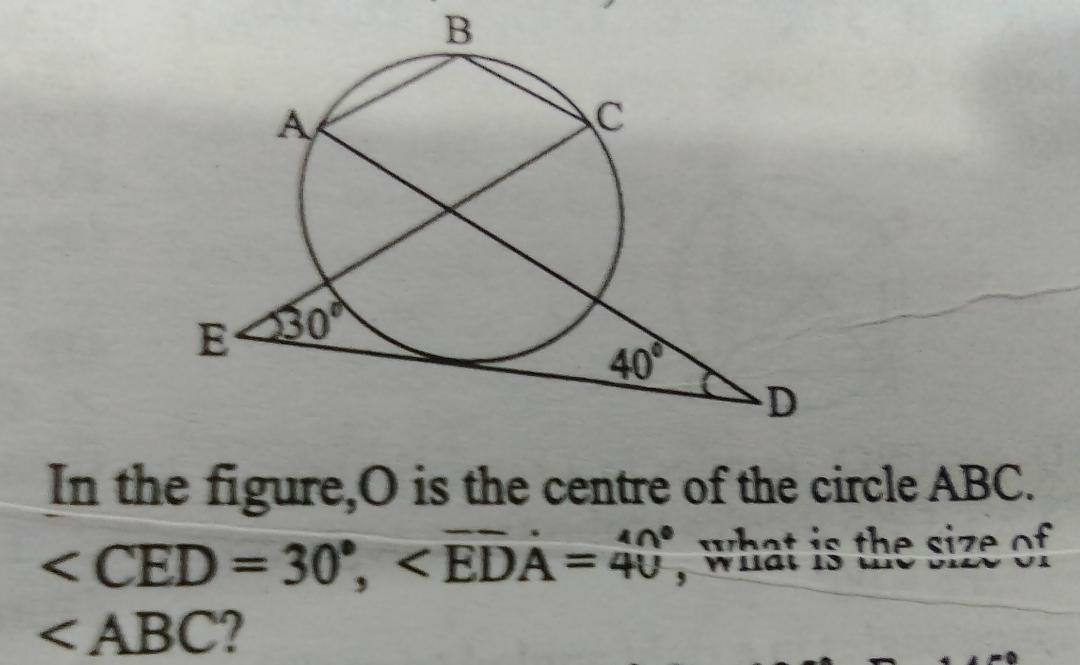
$${in}\:{the}\:{figure}\:{point}\:{O}\:{is}\:{not}\:{displayed}. \\ $$$${we}\:{assume}\:{O}\:{is}\:{the}\:{intersection}\:{of}\:{AD} \\ $$$${and}\:{EC}. \\ $$
Answered by mr W last updated on 24/Jan/20
Commented by mr W last updated on 24/Jan/20
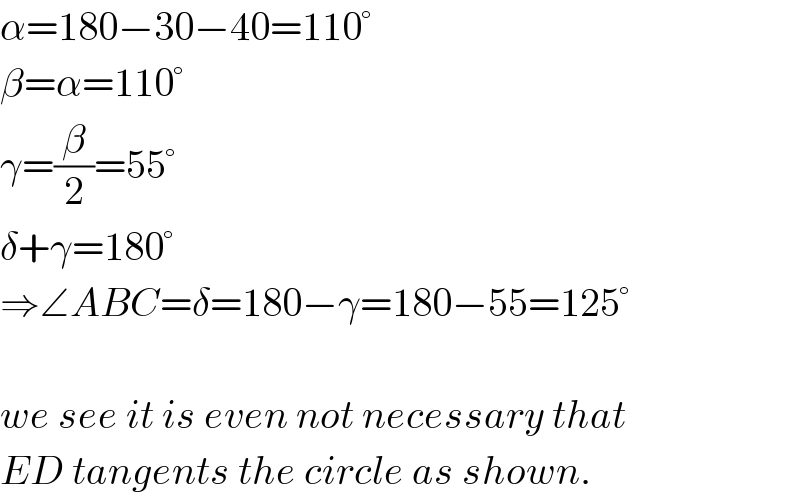
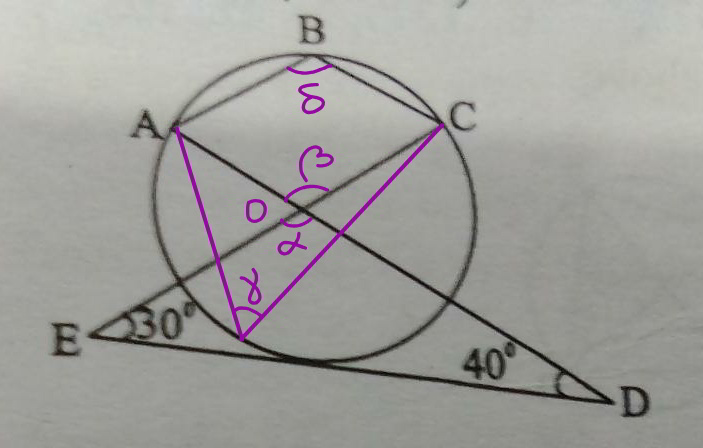
$$\alpha=\mathrm{180}−\mathrm{30}−\mathrm{40}=\mathrm{110}° \\ $$$$\beta=\alpha=\mathrm{110}° \\ $$$$\gamma=\frac{\beta}{\mathrm{2}}=\mathrm{55}° \\ $$$$\delta+\gamma=\mathrm{180}° \\ $$$$\Rightarrow\angle{ABC}=\delta=\mathrm{180}−\gamma=\mathrm{180}−\mathrm{55}=\mathrm{125}° \\ $$$$ \\ $$$${we}\:{see}\:{it}\:{is}\:{even}\:{not}\:{necessary}\:{that} \\ $$$${ED}\:{tangents}\:{the}\:{circle}\:{as}\:{shown}. \\ $$
Commented by TawaTawa last updated on 24/Jan/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}. \\ $$
Commented by mr W last updated on 24/Jan/20

$${is}\:{this}\:{solution}\:{correct}? \\ $$$${can}\:{you}\:{understand}\:{my}\:{solution}? \\ $$
Commented by TawaTawa last updated on 24/Jan/20
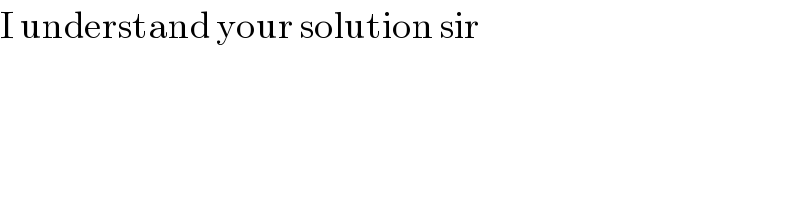
$$\mathrm{I}\:\mathrm{understand}\:\mathrm{your}\:\mathrm{solution}\:\mathrm{sir} \\ $$
Commented by TawaTawa last updated on 24/Jan/20

$$\alpha\:+\:\mathrm{30}\:+\:\mathrm{40}\:\:=\:\:\mathrm{180}\:\:\:\:\:\:\:\left(\mathrm{angle}\:\mathrm{in}\:\Delta\right) \\ $$$$\alpha\:\:=\:\:\beta\:\:\:\:\left(\mathrm{vertically}\:\mathrm{opposite}\:\mathrm{angle}\right) \\ $$$$\gamma\:+\:\delta\:\:=\:\:\mathrm{180}\:\:\left(\mathrm{opposite}\:\mathrm{angle}\:\mathrm{in}\:\mathrm{cyclic}\:\mathrm{quadrillaterals}\right) \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{will}\:\mathrm{use}\:\mathrm{your}\:\mathrm{workings}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{understand}. \\ $$
Commented by mr W last updated on 24/Jan/20
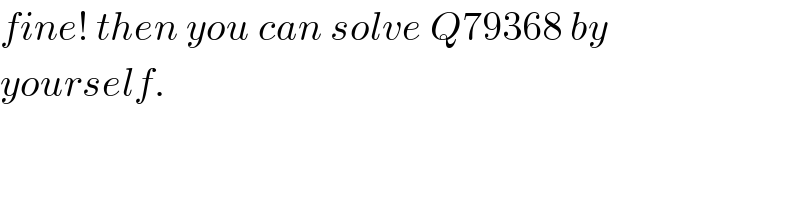
$${fine}!\:{then}\:{you}\:{can}\:{solve}\:{Q}\mathrm{79368}\:{by} \\ $$$${yourself}. \\ $$
Commented by TawaTawa last updated on 24/Jan/20

$$\mathrm{Let}\:\mathrm{me}\:\mathrm{try}\:\mathrm{sir}.\:\:\mathrm{Help}\:\mathrm{me}\:\mathrm{check}\:\mathrm{if}\:\mathrm{am}\:\mathrm{right}. \\ $$
